Integrates a smooth function using a nonadaptive rule.

Required Arguments

F — User-supplied FUNCTION to be integrated. The form is F(X), where
                                X – Independent variable.   (Input)
                                F – The function value.   (Output)
F must be declared EXTERNAL in the calling program.

A — Lower limit of integration.   (Input)

B — Upper limit of integration.   (Input)

RESULT — Estimate of the integral from A to B of F.   (Output)

Optional Arguments

ERRABS — Absolute accuracy desired.   (Input)
Default: ERRABS = 1.e-3 for single precision and 1.d-8 for double precision.

ERRREL — Relative accuracy desired.   (Input)
Default: ERRREL = 1.e-3 for single precision and 1.d-8 for double precision.

ERREST — Estimate of the absolute value of the error.   (Output)

FORTRAN 90 Interface

Generic:          CALL QDNG (F, A, B, RESULT [,…])

Specific:         The specific interface names are S_QDNG and D_QDNG.

FORTRAN 77 Interface

Single:            CALL QDNG (F, A, B, ERRABS, ERRREL, RESULT, ERREST)

Double:          The double precision name is DQDNG.

Description

The routine QDNG is designed to integrate smooth functions. This routine implements a nonadaptive quadrature procedure based on nested Paterson rules of order 10, 21, 43, and 87. These rules are positive quadrature rules with degree of accuracy 19, 31, 64, and 130, respectively. The routine QDNG applies these rules successively, estimating the error, until either the error estimate satisfies the user-supplied constraints or the last rule is applied. The routine QDNG is based on the routine QNG by Piessens et al. (1983).

This routine is not very robust, but for certain smooth functions it can be efficient. If QDNG should not perform well, we recommend the use of the IMSL routine QDAGS.

Comments

1.         Informational error
Type                                   Code

   4                  1       The maximum number of steps allowed have been taken. The integral is too difficult for QDNG.

2.         If EXACT is the exact value, QDNG attempts to find RESULT such that
ABS(EXACT − RESULT).LE.MAX(ERRABS, ERRREL * ABS(EXACT)). To specify only a relative error, set ERRABS to zero. Similarly, to specify only an absolute error, set ERRREL to zero.

3.         This routine is designed for efficiency, not robustness. If the above error is encountered, try QDAGS.

Example

The value of

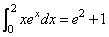
is estimated. The values of the actual and estimated error are machine dependent.

 

      USE QDNG_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    NOUT

      REAL       A, ABS, B, ERRABS, ERREST, ERROR, EXACT, EXP, &

                F, RESULT

      INTRINSIC  ABS, EXP

      EXTERNAL   F

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Set limits of integration

      A = 0.0

      B = 2.0

!                                 Set error tolerances

      ERRABS = 0.0

      CALL QDNG (F, A, B, RESULT, ERRABS=ERRABS, ERREST=ERREST)

!                                 Print results

      EXACT = 1.0 + EXP(2.0)

      ERROR = ABS(RESULT-EXACT)

      WRITE (NOUT,99999) RESULT, EXACT, ERREST, ERROR

99999 FORMAT (' Computed =', F8.3, 13X, ' Exact =', F8.3, /, /, &

            ' Error estimate =', 1PE10.3, 6X, 'Error =', 1PE10.3)

      END

!

      REAL FUNCTION F (X)

      REAL       X

      REAL       EXP

      INTRINSIC  EXP

      F = X*EXP(X)

      RETURN

      END

Output

 

Computed =   8.389              Exact =   8.389

Error estimate = 5.000E-05      Error = 9.537E-07

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260