SPLINE_FITTING

Weighted least-squares fitting by B-splines to discrete One-Dimensional data is performed.  Constraints on the spline or its derivatives are optional.  The spline function

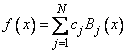
its derivatives, or the square root of its variance function are evaluated after the fitting.

Required Arguments

data = data(1:3,:)  (Input/Output)
An assumed-shape array with size(data,1) = 3.  The data are placed in the array: data(1,i) = 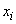, data(2,i) = 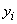, and data(3,i) = 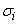, 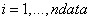. If the variances are not known but are proportional to an unknown value, users may set data(3,i) = 1, .

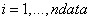knots = knots  (Input)
A derived type, ?_spline_knots, that defines the degree of the spline and the breakpoints for the data fitting interval.

Optional Arguments

constraints = spline_constraints  (Input)
A rank-1 array of derived type ?_spline_constraints that give constraints the output spline is to satisfy.

covariance = G  (Output)
An assumed-shape rank-2 array of the same precision as the data.  This output is the covariance matrix of the coefficients.  It is optionally used to evaluate the square root of the variance function.

iopt = iopt(:)  (Input/Output)
Derived type array with the same precision as the input array; used for passing optional data to spline_fitting. The options are as follows:

Packaged Options for spline_fitting

Prefix = None

Option Name

Option Value

 

Spline_fitting_tol_equal

1

 

Spline_fitting_tol_least

2

iopt(IO) = ?_options(spline_fitting_tol_equal, ?_value)
This resets the value for determining that equality constraint equations are rank-deficient.  The default is ?_value = 10-4.

iopt(IO) = ?_options(spline_fitting_tol_least, ?_value)
This resets the value for determining that least-squares equations are rank-deficient.  The default is ?_value = 10-4.

FORTRAN 90 Interface

Generic:          CALL SPLINE_FITTING (DATA, KNOTS [,…])

Specific:         The specific interface names are S_SPLINE_FITTING and D_SPLINE_FITTING.

Description

This routine has similar scope to CONFT found in IMSL (2003, pp 734-743).  We provide the square root of the variance function, but we do not provide for constraints on the integral of the spline.  The least-squares matrix problem for the coefficients is banded, with band-width equal to the spline order.  This fact is used to obtain an efficient solution algorithm when there are no constraints.  When constraints are present the routine solves a linear-least squares problem with equality and inequality constraints.  The processed least-squares equations result in a banded and upper triangular matrix, following accumulation of the spline fitting equations.  The algorithm used for solving the constrained least-squares system will handle rank-deficient problems.  A set of reference are available in Hanson (1995) and Lawson and Hanson (1995).  The CONFT routine uses QPROG (loc cit., p. 959), which requires that the least-squares equations be of full rank.

Fatal and Terminal Error Messages

See the messages.gls file for error messages for SPLINE_FITTING. These error mes­sages are numbered 1340-1367.

Example 1: Natural Cubic Spline Interpolation to Data

The function

 

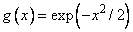
is interpolated by cubic splines on the grid of points

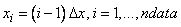
Those natural conditions are

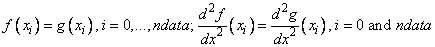
Our program checks the term 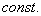 appearing in the maximum truncation error term

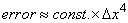
at a finer grid.

 

      USE spline_fitting_int

      USE show_int

      USE norm_int

      

      implicit none

 

! This is Example 1 for SPLINE_FITTING, Natural Spline

! Interpolation using cubic splines.  Use the function

! exp(-x**2/2) to generate samples.

 

      integer :: i

      integer, parameter :: ndata=24, nord=4, ndegree=nord-1, &

        nbkpt=ndata+2*ndegree, ncoeff=nbkpt-nord, nvalues=2*ndata

      real(kind(1e0)), parameter :: zero=0e0, one=1e0, half=5e-1

      real(kind(1e0)), parameter :: delta_x=0.15, delta_xv=0.4*delta_x

      real(kind(1e0)), target :: xdata(ndata), ydata(ndata), & 

            spline_data (3, ndata), bkpt(nbkpt), &

            ycheck(nvalues), coeff(ncoeff), &

            xvalues(nvalues), yvalues(nvalues), diffs

 

      real(kind(1e0)), pointer :: pointer_bkpt(:)

      type (s_spline_knots) break_points

      type (s_spline_constraints) constraints(2)

 

      xdata = (/((i-1)*delta_x, i=1,ndata)/) 

      ydata = exp(-half*xdata**2)

      xvalues =(/(0.03+(i-1)*delta_xv,i=1,nvalues)/)

      ycheck= exp(-half*xvalues**2)

      spline_data(1,:)=xdata 

      spline_data(2,:)=ydata

      spline_data(3,:)=one

 

! Define the knots for the interpolation problem.

         bkpt(1:ndegree) = (/(i*delta_x, i=-ndegree,-1)/) 

         bkpt(nord:nbkpt-ndegree) = xdata

         bkpt(nbkpt-ndegree+1:nbkpt) =  &

         (/(xdata(ndata)+i*delta_x, i=1,ndegree)/)

 

! Assign the degree of the polynomial and the knots.

      pointer_bkpt => bkpt

      break_points=s_spline_knots(ndegree, pointer_bkpt)

 

! These are the natural conditions for interpolating cubic

! splines.  The derivatives match those of the interpolating

! function at the ends.

      constraints(1)=spline_constraints &

         (derivative=2, point=bkpt(nord), type='==', value=-one)

      constraints(2)=spline_constraints &

         (derivative=2,point=bkpt(nbkpt-ndegree), type= '==', &

         value=(-one+xdata(ndata)**2)*ydata(ndata))

 

      coeff = spline_fitting(data=spline_data, knots=break_points,&

             constraints=constraints)

      yvalues=spline_values(0, xvalues, break_points, coeff)

 

      diffs=norm(yvalues-ycheck,huge(1))/delta_x**nord 

 

      if (diffs <= one) then

        write(*,*) 'Example 1 for SPLINE_FITTING is correct.'

      end if

      end 

Output

 

Example 1 for SPLINE_FITTING is correct.

Additional Examples

Example 2: Shaping a Curve and its Derivatives

The function

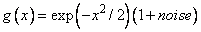
is fit by cubic splines on the grid of equally spaced points

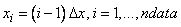
The term noise is uniform random numbers from the normalized interval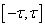
, where 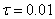.  The spline curve is constrained to be convex down for for 0 ≤ x ≤ 1 convex upward for 1< x ≤ 4, and have the second derivative exactly equal to the value zero at 
x = 1.  The first derivative is constrained with the value zero at x = 0  and is non-negative at the right and of the interval, x = 4.  A sample table of independent variables, second derivatives and square root of  variance function values is printed.

 

      use spline_fitting_int

      use show_int

      use rand_int

      use norm_int

 

      implicit none

 

! This is Example 2 for SPLINE_FITTING. Use 1st and 2nd derivative

! constraints to shape the splines.

 

      integer :: i, icurv

      integer, parameter :: nbkptin=13, nord=4, ndegree=nord-1, &

             nbkpt=nbkptin+2*ndegree, ndata=21, ncoeff=nbkpt-nord

      real(kind(1e0)), parameter :: zero=0e0, one=1e0, half=5e-1

      real(kind(1e0)), parameter :: range=4.0, ratio=0.02, tol=ratio*half

      real(kind(1e0)), parameter :: delta_x=range/(ndata-1), &
      delta_b=range/(nbkptin-1)

      real(kind(1e0)), target :: xdata(ndata), ydata(ndata), ynoise(ndata),& 

            sddata(ndata), spline_data (3, ndata), bkpt(nbkpt), &

            values(ndata), derivat1(ndata), derivat2(ndata), &

            coeff(ncoeff), root_variance(ndata), diffs

      real(kind(1e0)), dimension(ncoeff,ncoeff) :: sigma_squared

 

      real(kind(1e0)), pointer :: pointer_bkpt(:)

      type (s_spline_knots) break_points

      type (s_spline_constraints) constraints(nbkptin+2)

      xdata = (/((i-1)*delta_x, i=1,ndata)/) 

      ydata = exp(-half*xdata**2) 

      ynoise = ratio*ydata*(rand(ynoise)-half)

      ydata = ydata+ynoise

      sddata = ynoise

      spline_data(1,:)=xdata

      spline_data(2,:)=ydata

      spline_data(3,:)=sddata

 

      bkpt=(/((i-nord)*delta_b, i=1,nbkpt)/) 

 

! Assign the degree of the polynomial and the knots.

      pointer_bkpt => bkpt

      break_points=s_spline_knots(ndegree, pointer_bkpt)

 

      icurv=int(one/delta_b)+1

 

! At first shape the curve to be convex down.      

      do i=1,icurv-1

        constraints(i)=spline_constraints &

 (derivative=2, point=bkpt(i+ndegree), type='<=', value=zero)

      end do

 

! Force a curvature change.

      constraints(icurv)=spline_constraints &

 (derivative=2, point=bkpt(icurv+ndegree), type='==', value=zero)

 

! Finally, shape the curve to be convex up.

      do i=icurv+1,nbkptin

        constraints(i)=spline_constraints &

 (derivative=2, point=bkpt(i+ndegree), type='>=', value=zero)

      end do

 

! Make the slope zero and value non-negative at right.

      constraints(nbkptin+1)=spline_constraints &

 (derivative=1, point=bkpt(nord), type='==', value=zero)

      constraints(nbkptin+2)=spline_constraints &

 (derivative=0, point=bkpt(nbkptin+ndegree), type='>=', value=zero)

 

      coeff = spline_fitting(data=spline_data, knots=break_points, &

              constraints=constraints, covariance=sigma_squared)

 

!     Compute value, first two derivatives and the variance.

      values=spline_values(0, xdata, break_points, coeff)

      root_variance=spline_values(0, xdata, break_points, coeff, &

                             covariance=sigma_squared)

      derivat1=spline_values(1, xdata, break_points, coeff)

      derivat2=spline_values(2, xdata, break_points, coeff)

  

      call show(reshape((/xdata, derivat2, root_variance/),(/ndata,3/)),&

"The x values, 2-nd derivatives, and square root of variance.")

 

! See that differences are relatively small and the curve has

! the right shape and signs.      

      diffs=norm(values-ydata)/norm(ydata)

      if (all(values > zero) .and. all(derivat1 < epsilon(zero))&

         .and. diffs <= tol) then

        write(*,*) 'Example 2 for SPLINE_FITTING is correct.'

      end if

 

      end 

Output

 

Example 2 for SPLINE_FITTING is correct.

Example 3: Splines Model a Random Number Generator

The function

is an unnormalized probability distribution.  This function is similar to the standard Normal distribution, with specific choices for the mean and variance, except that it is truncated.  Our algorithm interpolates g(x) with a natural cubic spline, f(x).  The cumulative distribution is approximated by precise evaluation of the function

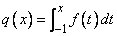
Gauss-Legendre quadrature formulas, IMSL (1994, pp. 621-626), of order two are used on each polynomial piece of f(t)  to evaluate q(x) cheaply.  After normalizing the cubic spline so that
q(1) = 1, we may then generate random numbers according to the distribution 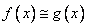.  The values of  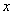are evaluated by solving q(x) = u, -1 < x < 1.  Here 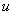 is a uniform random sample.  Newton's method, for a vector of unknowns, is used for the solution algorithm.  Recalling the relation

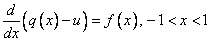
we believe this illustrates a method for generating a vector of random numbers according to a continuous distribution function having finite support.

 

       use spline_fitting_int

       use linear_operators

       use Numerical_Libraries

      

       implicit none

 

! This is Example 3 for SPLINE_FITTING.  Use splines to

! generate random (almost normal) numbers.  The normal distribution

! function has support (-1,+1), and is zero outside this interval.

! The variance is 0.5.

 

       integer i, niterat

        integer, parameter :: iweight=1, nfix=0, nord=4, ndata=50

        integer, parameter :: nquad=(nord+1)/2, ndegree=nord-1

        integer, parameter :: nbkpt=ndata+2*ndegree, ncoeff=nbkpt-nord

        integer, parameter :: last=nbkpt-ndegree, n_samples=1000

        integer, parameter :: limit=10

       real(kind(1e0)), dimension(n_samples) :: fn, rn, x, alpha_x, beta_x

        INTEGER LEFT_OF(n_samples)

       real(kind(1e0)), parameter :: one=1e0, half=5e-1, zero=0e0, two=2e0

       real(kind(1e0)), parameter :: delta_x=two/(ndata-1)

        real(kind(1e0)), parameter :: qalpha=zero, qbeta=zero, domain=two 

        real(kind(1e0)) qx(nquad), qxi(nquad), qw(nquad), qxfix(nquad)

        real(kind(1e0)) alpha_, beta_, quad(0:ndata-1)

        real(kind(1e0)), target :: xdata(ndata), ydata(ndata),&
        coeff(ncoeff), spline_data(3, ndata), bkpt(nbkpt)

 

        real(kind(1e0)), pointer :: pointer_bkpt(:)

        type (s_spline_knots) break_points

        type (s_spline_constraints) constraints(2)

 

! Approximate the probability density function by splines.

        xdata = (/(-one+(i-1)*delta_x, i=1,ndata)/) 

        ydata = exp(-half*xdata**2)

 

        spline_data(1,:)=xdata

        spline_data(2,:)=ydata

        spline_data(3,:)=one

 

        bkpt=(/(-one+(i-nord)*delta_x, i=1,nbkpt)/) 

 

! Assign the degree of the polynomial and the knots.

      pointer_bkpt => bkpt

      break_points=s_spline_knots(ndegree, pointer_bkpt)

 

! Define the natural derivatives constraints:

        constraints(1)=spline_constraints &

          (derivative=2, point=bkpt(nord), type='==', &

          value=(-one+xdata(1)**2)*ydata(1))

        constraints(2)=spline_constraints &

          (derivative=2, point=bkpt(last), type='==', &

          value=(-one+xdata(ndata)**2)*ydata(ndata))

 

! Obtain the spline coefficients.

        coeff=spline_fitting(data=spline_data, knots=break_points,&

        constraints=constraints)

 

! Compute the evaluation points 'qx(*)' and weights 'qw(*)' for 

! the Gauss-Legendre quadrature.  This will give a precise

! quadrature for polynomials of degree <= nquad*2.

        call gqrul(nquad, iweight, qalpha, qbeta, nfix, qxfix, qx, qw)

 

! Compute pieces of the accumulated distribution function: 

        quad(0)=zero

       do i=1, ndata-1

          alpha_= (bkpt(nord+i)-bkpt(ndegree+i))*half

          beta_ = (bkpt(nord+i)+bkpt(ndegree+i))*half

 

! Normalized abscissas are stretched to each spline interval.

! Each polynomial piece is integrated and accumulated.

          qxi = alpha_*qx+beta_

          quad(i) = sum(qw*spline_values(0, qxi, break_points,&
      coeff))*alpha_&

                  + quad(i-1)

       end do

 

! Normalize the coefficients and partial integrals so that the

! total integral has the value one.

        coeff=coeff/quad(ndata-1); quad=quad/quad(ndata-1)

        rn=rand(rn) 

        x=zero; niterat=0

 

       solve_equation: do

 

! Find the intervals where the x values are located.

          LEFT_OF=NDEGREE; I=NDEGREE

            do

               I=I+1; if(I >= LAST) EXIT

               WHERE(x >= BKPT(I))LEFT_OF = LEFT_OF+1

            end do

 

! Use Newton's method to solve the nonlinear equation:

! accumulated_distribution_function - random_number = 0.

            alpha_x = (x-bkpt(LEFT_OF))*half

            beta_x  = (x+bkpt(LEFT_OF))*half

            FN=QUAD(LEFT_OF-NORD)-RN

            DO I=1,NQUAD

               FN=FN+QW(I)*spline_values(0, alpha_x*QX(I)+beta_x,&

                     break_points, coeff)*alpha_x

            END DO

 

! This is the Newton method update step:

            x=x-fn/spline_values(0, x, break_points, coeff)

            niterat=niterat+1

 

! Constrain the values so they fall back into the interval.

! Newton's method may give approximates outside the interval.

            where(x <= -one .or. x >= one) x=zero

 

            if(norm(fn,1) <= sqrt(epsilon(one))*norm(x,1))&

              exit solve_equation

       end do solve_equation

 

! Check that Newton's method converges. 

 

        if (niterat <= limit) then

          write (*,*) 'Example 3 for SPLINE_FITTING is correct.'

        end if

 

       end 

Output

 

Example 3 for SPLINE_FITTING is correct.

Example 4: Represent a Periodic Curve

The curve tracing the edge of a rectangular box, traversed in a counter-clockwise direction, is parameterized with a spline representation for each coordinate function, (x(t), y(t)).  The functions are constrained to be periodic at the ends of the parameter interval.  Since the perimeter arcs are piece-wise linear functions, the degree of the splines is the value one.  Some breakpoints are chosen so they correspond to corners of the box, where the derivatives of the coordinate functions are discontinuous.  The value of this representation is that for each t the splines representing
(x(t), y(t)) are points on the perimeter of the box.  This “eases” the complexity of evaluating the edge of the box.  This example illustrates a method for representing the edge of a domain in two dimensions, bounded by a periodic curve.

 

      use spline_fitting_int

      use norm_int

 

      implicit none

 

! This is Example 4 for SPLINE_FITTING. Use piecewise-linear

! splines to represent the perimeter of a rectangular box.

 

      integer i, j 

      integer, parameter :: nbkpt=9, nord=2, ndegree=nord-1, &

               ncoeff=nbkpt-nord, ndata=7, ngrid=100, &

               nvalues=(ndata-1)*ngrid

      real(kind(1e0)), parameter :: zero=0e0, one=1e0

      real(kind(1e0)), parameter ::  delta_t=one, delta_b=one, delta_v=0.01

      real(kind(1e0)) delta_x, delta_y

      real(kind(1e0)), dimension(ndata) ::  sddata=one,  &

! These are redundant coordinates on the edge of the box.

             xdata=(/0.0, 1.0, 2.0, 2.0, 1.0, 0.0, 0.0/), &

             ydata=(/0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0/)

      real(kind(1e0)) tdata(ndata), xspline_data(3, ndata), &

            yspline_data(3, ndata), tvalues(nvalues), &

            xvalues(nvalues), yvalues(nvalues), xcoeff(ncoeff), &

            ycoeff(ncoeff), xcheck(nvalues), ycheck(nvalues), diffs

      real(kind(1e0)), target :: bkpt(nbkpt)

      real(kind(1e0)), pointer :: pointer_bkpt(:)

      type (s_spline_knots) break_points

      type (s_spline_constraints) constraints(1)

 

      tdata = (/((i-1)*delta_t, i=1,ndata)/) 

      xspline_data(1,:)=tdata; yspline_data(1,:)=tdata 

      xspline_data(2,:)=xdata; yspline_data(2,:)=ydata

      xspline_data(3,:)=sddata; yspline_data(3,:)=sddata

 

      bkpt(nord:nbkpt-ndegree)=(/((i-nord)*delta_b,  &

                                  i=nord, nbkpt-ndegree)/) 

! Collapse the outside knots.

      bkpt(1:ndegree)=bkpt(nord)  

      bkpt(nbkpt-ndegree+1:nbkpt)=bkpt(nbkpt-ndegree)  

   

! Assign the degree of the polynomial and the knots.

      pointer_bkpt => bkpt

      break_points=s_spline_knots(ndegree, pointer_bkpt)

 

! Make the two parametric curves also periodic.

      constraints(1)=spline_constraints &

        (derivative=0, point=bkpt(nord), type='.=.', &

        value=bkpt(nbkpt-ndegree))

 

      xcoeff = spline_fitting(data=xspline_data, knots=break_points, &

                              constraints=constraints)

      ycoeff = spline_fitting(data=yspline_data, knots=break_points, &

                              constraints=constraints)

 

! Use the splines to compute the coordinates of points along the perimeter. 

! Compare them with the coordinates of the edge points. 

      tvalues= (/((i-1)*delta_v, i=1,nvalues)/) 

      xvalues=spline_values(0, tvalues, break_points, xcoeff)

      yvalues=spline_values(0, tvalues, break_points, ycoeff)

      do i=1, nvalues

        j=(i-1)/ngrid+1   

        delta_x=(xdata(j+1)-xdata(j))/ngrid

       delta_y=(ydata(j+1)-ydata(j))/ngrid

        xcheck(i)=xdata(j)+mod(i+ngrid-1,ngrid)*delta_x      

        ycheck(i)=ydata(j)+mod(i+ngrid-1,ngrid)*delta_y      

      end do

 

      diffs=norm(xvalues-xcheck,1)/norm(xcheck,1)+&

           norm(yvalues-ycheck,1)/norm(ycheck,1)

      if (diffs <= sqrt(epsilon(one))) then

        write(*,*) 'Example 4 for SPLINE_FITTING is correct.'

      end if

      

      end 

Output

 

Example 4 for SPLINE_FITTING is correct.

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260