This function evaluates the hypergeometric cumulative distribution function.

Function Return Value

HYPDF — Function value, the probability that a hypergeometric random variable takes a value less than or equal to K.   (Output)
HYPDF is the probability that K or fewer defectives occur in a sample of size N drawn from a lot of size L that contains M defectives.
See Comment 1.

Required Arguments

K — Argument for which the hypergeometric cumulative distribution function is to be evaluated.   (Input)

N — Sample size.   (Input)
N must be greater than zero and greater than or equal to K.

M — Number of defectives in the lot.   (Input)

L — Lot size.   (Input)
L must be greater than or equal to N and M.

FORTRAN 90 Interface

Generic:                              HYPDF (K, N, M, L)

Specific:                             The specific interface names are S_HYPDF and D_HYPDF.

FORTRAN 77 Interface

Single:                                HYPDF (K, N, M, L)

Double:                              The double precision name is DHYPDF.

Description

The function HYPDF evaluates the cumulative distribution function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is

 

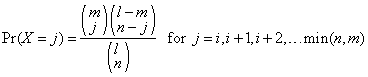
where i = max(0, n − l + m).

If k is greater than or equal to i and less than or equal to min(n, m), HYPDF sums the terms in this expression for j going from i up to k. Otherwise, HYPDF returns 0 or 1, as appropriate. So, as to avoid rounding in the accumulation, HYPDF performs the summation differently depending on whether or not k is greater than the mode of the distribution, which is the greatest integer less than or equal to (m + 1)(n + 1)/(l + 2).

Comments

1.         If the generic version of this function is used, the immediate result must be stored in a variable before use in an expression. For example:

X = HYPDF (K, N, M, L)

Y = SQRT(X)

            must be used rather than

Y = SQRT(HYPDF(K, N, M, L))

            If this is too much of a restriction on the programmer, then the specific name can be used without this restriction.

2.         Informational errors

Type Code

1         5                  The input argument, K, is less than zero.

1         6                  The input argument, K, is greater than the sample size.

Example

Suppose X is a hypergeometric random variable with n = 100, l = 1000, and m = 70. In this example, we evaluate the distribution function at 7.

 

      USE UMACH_INT

      USE HYPDF_INT

      IMPLICIT   NONE

      INTEGER    K, L, M, N, NOUT

      REAL       DF

!

      CALL UMACH (2, NOUT)

      K  = 7

      N  = 100

      L  = 1000

      M  = 70

      DF = HYPDF(K,N,M,L)

      WRITE (NOUT,99999) DF

99999 FORMAT (' The probability that X is less than or equal to 7 is ' &

            , F6.4)

      END

Output

 

The probability that X is less than or equal to 7 is 0.5995

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260