Sfun (JMSL Numerical Library (jmsl) 2021.0.0 API)

java.lang.Object
- com.imsl.math.Sfun

```
public class Sfun
extends Object
```
Collection of special functions.

See Also:

Example

Field Summary

Fields
Modifier and Type Field and Description

static double EPSILON_LARGE
The largest relative spacing for doubles.

static double EPSILON_SMALL
The smallest relative spacing for doubles.

Fields
Modifier and Type	Field and Description
`static double`	`EPSILON_LARGE` The largest relative spacing for doubles.
`static double`	`EPSILON_SMALL` The smallest relative spacing for doubles.

Method Summary

All Methods Static Methods Concrete Methods Deprecated Methods
Modifier and Type	Method and Description
`static double`	`beta(double a, double b)` Returns the value of the beta function.
`static double`	`betaIncomplete(double x, double p, double q)` Returns the incomplete beta function ratio.
`static double`	`cot(double x)` Returns the cotangent of a `double`.
`static double`	`erf(double x)` Returns the error function of a `double`.
`static double`	`erfc(double x)` Returns the complementary error function of a `double`.
`static double`	`erfce(double x)` Returns the exponentially scaled complementary error function.
`static double`	`erfcInverse(double x)` Returns the inverse of the complementary error function.
`static double`	`erfInverse(double x)` Returns the inverse of the error function.
`static double`	`fact(int n)` Returns the factorial of an integer.
`static double`	`gamma(double x)` Returns the Gamma function of a `double`.
`static double`	`gammaIncomplete(double a, double x)` Evaluates the incomplete gamma function.
`static double`	`log10(double x)` Returns the common (base 10) logarithm of a `double`.
`static double`	`logBeta(double a, double b)` Returns the logarithm of the beta function.
`static double`	`logGamma(double x)` Returns the logarithm of the absolute value of the Gamma function.
`static double`	`logGammaCorrection(double x)` Deprecated.
`static double`	`poch(double a, double x)` Returns a generalization of Pochhammer's symbol.
`static double`	`psi(double x)` Returns the derivative of the log gamma function, also called the digamma function.
`static double`	`psi1(double x)` Returns the $\psi _1 $ function, also known as the trigamma function.
`static double`	`r9lgmc(double x)` Deprecated.
`static double`	`sign(double x, double y)` Returns the value of x with the sign of y.

Methods inherited from class java.lang.Object
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

- Field Detail
  - EPSILON_SMALL
```
public static final double EPSILON_SMALL
```
    The smallest relative spacing for doubles.
    
    See Also:
    
    Constant Field Values
  - EPSILON_LARGE
```
public static final double EPSILON_LARGE
```
    The largest relative spacing for doubles.
    
    See Also:
    
    Constant Field Values
- Method Detail
  - cot
```
public static double cot(double x)
```
    Returns the cotangent of a double.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the cotangent of x. If x is NaN, the result is NaN.
  - log10
```
public static double log10(double x)
```
    Returns the common (base 10) logarithm of a double.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the common logarithm of x.
  - sign
```
public static double sign(double x,
                          double y)
```
    Returns the value of x with the sign of y.
    
    Parameters:
    
    x - a double value
    
    y - a double value
    
    Returns:
    
    a double value specifying the absolute value of x and the sign of y.
  - fact
```
public static double fact(int n)
```
    Returns the factorial of an integer.
    
    Parameters:
    
    n - an int value
    
    Returns:
    
    a double value specifying the factorial of n, n!. If n is negative, the result is NaN.
  - gamma
```
public static double gamma(double x)
```
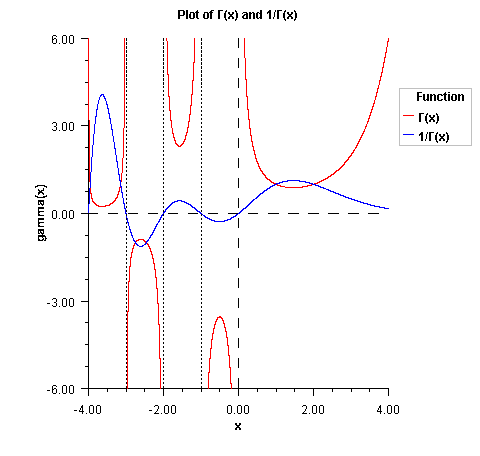
    Returns the Gamma function of a double.
    The gamma function, $\Gamma (x)$, is defined to be
    
    $$\Gamma \left( x \right) = \int_0^\infty {t^{x - 1} } e^{ - t} dt \,\,\,\, for \, x \gt 0$$
    
    For $x \lt 0$, the above definition is extended by analytic continuation.
    
    The gamma function is not defined for integers less than or equal to zero. Also, the argument x must be greater than -170.56 so that $\Gamma (x)$ does not underflow, and x must be less than 171.64 so that $\Gamma (x)$ does not overflow. The underflow limit occurs first for arguments that are close to large negative half integers. Even though other arguments away from these half integers may yield machine-representable values of $\Gamma (x)$, such arguments are considered illegal. Users who need such values should use the log gamma. Finally, the argument should not be so close to a negative integer that the result is less accurate than half precision.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the Gamma function of x. If x is a negative integer, the result is NaN.
    
    See Also:
    
    Example
  - psi1
```
public static double psi1(double x)
```
    Returns the $\psi _1 $ function, also known as the trigamma function.
    The trigamma function, $\psi _1 (x)$, is defined to be
    
    $$\psi _1\left(x\right)=\frac{d^2}{dx^2}\ln \Gamma(x)$$
    
    The trigamma function is not defined for integers less than or equal to zero.
    
    Parameters:
    
    x - a double value, the point at which the trigamma function is to be evaluated.
    
    Returns:
    
    a double value specifying the trigamma function of x. If x is a negative integer or zero, the result is NaN.
    
    See Also:
    
    Example
  - logGamma
```
public static double logGamma(double x)
```
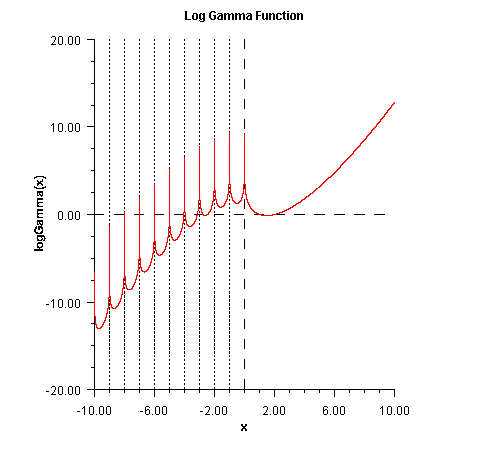
    Returns the logarithm of the absolute value of the Gamma function.
    Method logGamma computes $\ln\left|{\Gamma(x)} \right|$. See Sfun.gamma(double) for the definition of $\Gamma(x)$.
    
    The gamma function is not defined for integers less than or equal to zero. Also, $\left| x \right|$ must not be so large that the result overflows. Neither should x be so close to a negative integer that the accuracy is worse than half precision.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double, the natural logarithm of the Gamma function of x. If x is a negative integer, the result is NaN.
    
    See Also:
    
    Example
  - r9lgmc
```
public static double r9lgmc(double x)
```
    Deprecated.
    
    Returns the log gamma correction term for argument values greater than or equal to 10.0.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the log gamma correction term.
  - logGammaCorrection
```
public static double logGammaCorrection(double x)
```
    Deprecated.
    
    Returns the logarithm of the gamma correction term for argument values greater than or equal to 10.0.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double containing the logarithm of the correction term.
  - beta
```
public static double beta(double a,
                          double b)
```
    Returns the value of the beta function. The beta function is defined to be
    $$\beta(a,b)={{\Gamma(a)\Gamma(b)}\over {\Gamma(a+b)}}=\int_0^1{t^{a-1}}(1-t)^{b-1}dt$$
    See Sfun.gamma(double) for the definition of $\Gamma\left(x \right)$.
    The method beta requires that both arguments be positive.
    
    Parameters:
    
    a - a double value
    
    b - a double value
    
    Returns:
    
    a double value specifying the Beta function
    
    See Also:
    
    Example
  - logBeta
```
public static double logBeta(double a,
                             double b)
```
    Returns the logarithm of the beta function.
    Method logBeta computes ${\rm ln}\,\beta\left( {a,b}\right)={\rm ln}\,\beta\left({b,a}\right)$. See Sfun.beta(double, double) for the definition of $\beta\left({a,b}\right) $.
    
    logBeta is defined for a $\gt$ 0 and b $\gt$ 0. It returns accurate results even when a or b is very small. It can overflow for very large arguments; this error condition is not detected except by the computer hardware.
    
    Parameters:
    
    a - a double value
    
    b - a double value
    
    Returns:
    
    a double value specifying the natural logarithm of the beta function.
    
    See Also:
    
    Example
  - betaIncomplete
```
public static double betaIncomplete(double x,
                                    double p,
                                    double q)
```
    Returns the incomplete beta function ratio. The incomplete beta function is defined to be
    $$I_x(p,\,\,q)={{\beta_x(p,\, \,q)}\over{\beta(p,\,\,q)}}={1\over{\beta(p,\,\,q)}}\int_0^x{t^{p-1}}(1-t )^{q-1}dt\,\,{\rm{for}}\,\,0\le x\le 1,\,p>0,\,q>0$$
    See Sfun.beta(double, double) for the definition of $\beta\left({p,\,q} \right)$.
    The parameters p and q must both be greater than zero. The argument x must lie in the range 0 to 1. The incomplete beta function can underflow for sufficiently small x and large p; however, this underflow is not reported as an error. Instead, the value zero is returned as the function value.
    
    The method betaIncomplete is based on the work of Bosten and Battiste (1974).
    
    Parameters:
    
    x - a double value specifying the upper limit of integration. It must be in the interval [0,1] inclusive.
    
    p - a double value specifying the first Beta parameter. It must be positive.
    
    q - a double value specifying the second Beta parameter. It must be positive.
    
    Returns:
    
    a double value specifying the incomplete Beta function ratio
    
    See Also:
    
    Example
  - poch
```
public static double poch(double a,
                          double x)
```
    Returns a generalization of Pochhammer's symbol.
    Method poch evaluates Pochhammer's symbol $(a)_n = (a)(a - 1)\ldots (a - n + 1)$ for n a nonnegative integer. Pochhammer's generalized symbol is defined to be
    
    $$\left(a\right)_x=\frac{{\Gamma\left({a+x} \right)}}{{\Gamma\left(a\right)}}$$
    
    See Sfun.gamma(double) for the definition of $\Gamma (x)$.
    
    Note that a straightforward evaluation of Pochhammer's generalized symbol with either gamma or log gamma functions can be especially unreliable when a is large or x is small.
    
    Substantial loss can occur if a + x or a are close to a negative integer unless $\left|x\right|$ is sufficiently small. To insure that the result does not overflow or underflow, one can keep the arguments a and a + x well within the range dictated by the gamma function method gamma or one can keep $\left|x\right|$ small whenever a is large. poch also works for a variety of arguments outside these rough limits, but any more general limits that are also useful are difficult to specify.
    
    Parameters:
    
    a - a double value specifying the first argument
    
    x - a double value specifying the second, differential argument
    
    Returns:
    
    a double value specifying the generalized Pochhammer symbol, $ \frac{{\Gamma\left({a+x} \right)}}{{\Gamma\left(a\right)}}$
    
    See Also:
    
    Example
  - erf
```
public static double erf(double x)
```
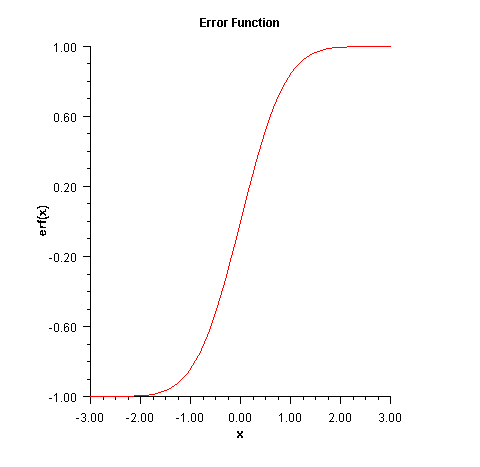
    Returns the error function of a double.
    The error function method, erf(x), is defined to be
    
    $${\rm{erf}}\left(x\right)={2\over{\sqrt\pi}} \int_0^x{e^{-t^2}}dt$$
    
    All values of x are legal.
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the error function of x
    
    See Also:
    
    Example
  - erfc
```
public static double erfc(double x)
```
    Returns the complementary error function of a double.
    The complementary error function method, erfc (x), is defined to be
    
    $${\rm{erfc}}\left(x\right)={2\over{\sqrt\pi}} \int_x^\infty{e^{-t^2}}dt$$
    
    The argument x must not be so large that the result underflows. Approximately, x should be less than
    
    $${\left[-\ln\left({\sqrt{\pi}}s\right)\right]} ^{1/2}$$
    
    where s = Double.MIN_VALUE is the smallest representable positive floating-point number.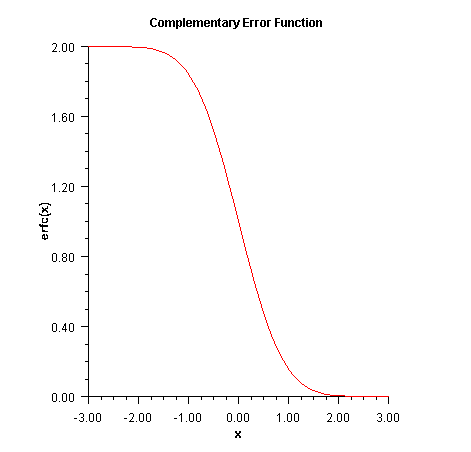
    
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the complementary error function of x
    
    See Also:
    
    Example
  - erfInverse
```
public static double erfInverse(double x)
```
    Returns the inverse of the error function.
    The erfInverse method computes the inverse of the error function erf x, defined in Sfun.erf(double).
    
    The method erfInverse(x) is defined for $x_{\it max}\lt\left|x\right|\lt 1$, then the answer will be less accurate than half precision. Very approximately,
    
    $$x_{\max}\approx 1-\sqrt{\varepsilon /\left({ 4\pi}\right)}$$
    
    where $\varepsilon$ is the machine precision (approximately 1.11e-16).
    
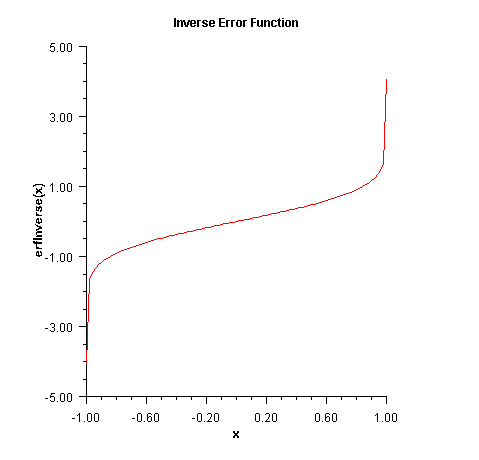
    Parameters:
    
    x - a double value
    
    Returns:
    
    a double value specifying the inverse of the error function of x.
    
    See Also:
    
    Example
  - erfcInverse
```
public static double erfcInverse(double x)
```
    Returns the inverse of the complementary error function.
    The erfcinverse method computes the inverse of the complementary error function erfc x, defined in erfc.
    
    erfcinverse(x) is defined for $0\lt x\lt 2 $. If $x_{\max}\lt x\lt 2$, then the answer will be less accurate than half precision. Very approximately,
    
    $$x_{\it max}\approx 2-\sqrt{\varepsilon /(4\ pi)}$$
    
    where $\varepsilon$ = machine precision (approximately 1.11e-16).
    
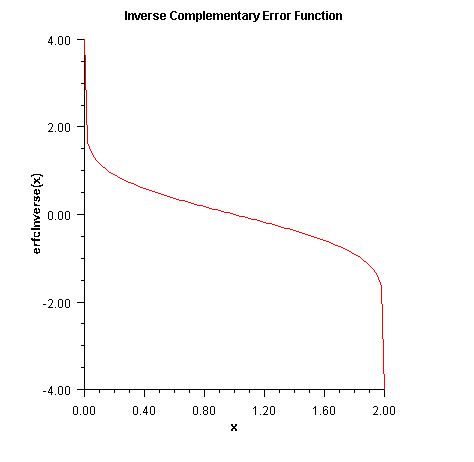
    Parameters:
    
    x - a double value, $0\le x\le 2$.
    
    Returns:
    
    a double value specifying the inverse of the error function of x.
    
    See Also:
    
    Example
  - erfce
```
public static double erfce(double x)
```
    Returns the exponentially scaled complementary error function.
    The exponentially scaled complementary error function is defined as
    $$e^{x^{2}}\mathrm{erfc}(x)$$
    where erfc(x) is the complementary error function. See Sfun.erfc(double) for its definition.
    
    To prevent the answer from underflowing, x must be greater than
    $$x_{\mathrm{min}}\simeq-\sqrt{\ln(b/2)} = -26.618735713751487$$
    where b = Double.MAX_VALUE is the largest representable double precision number.
    
    Parameters:
    
    x - a double value for which the function value is desired.
    
    Returns:
    
    a double value specifying the exponentially scaled complementary error function of x.
  - gammaIncomplete
```
public static double gammaIncomplete(double a,
                                     double x)
```
    Evaluates the incomplete gamma function.
    The lower limit of integration of the incomplete gamma function, $\gamma(a,x)$, is defined to be
    $$\gamma(a,x)=\int_{0}^{x}t^{a-1}e^{-t}dt\;\;\;\; \mbox{for }x\ge0\mbox{ and }a>0$$
    Although $\gamma(a,x)$ is well defined for $x>-\infty$, this algorithm does not calculate $\gamma(a,x)$ for negative x. For large a and sufficiently large x, $\gamma(a,x)$ may overflow. $\gamma(a,x)$ is bounded by $ \Gamma(a)$, and users may find this bound a useful guide in determining legal values for a.
    
    Note that the upper limit of integration of the incomplete gamma, $\Gamma(a,x)$, is defined to be
    $$\Gamma(a,x)=\int_{x}^{\infty}t^{a-1}e^{-t}dt $$
    Therefore, by definition, the two incomplete gamma function forms satisfy the relationship
    $$\Gamma(a,x)+\gamma(a,x)=\Gamma(a)$$
    
    Parameters:
    
    a - a double value representing the integrand exponent parameter of the incomplete gamma function. It must be positive.
    
    x - a double value specifying the point at which the incomplete gamma function is to be evaluated. It must be nonnegative.
    
    Returns:
    
    a double value specifying the incomplete gamma function.
  - psi
```
public static double psi(double x)
```
    Returns the derivative of the log gamma function, also called the digamma function.
    The psi function is defined to be $$\psi(x)= \frac{d}{dx}\ln\Gamma(x)=\frac{\Gamma'(x)}{\Gamma(x)}$$ See Sfun.gamma(double) for the definition of $\Gamma(x)$.
    
    The argument x must not be exactly zero or a negative integer, or $\psi(x)$ is undefined. Also, x must not be too close to a negative integer such that the accuracy of the result is less than half precision.
    
    Parameters:
    
    x - a double value, the point at which the digamma function is to be evaluated.
    
    Returns:
    
    a double value specifying the logarithmic derivative of the gamma function of x. If x is a zero or a negative integer, the result is NaN. If x is too close to a negative integer the accuracy of the result will be less than half precision.
    
    See Also:
    
    Example