CategoricalGenLinModel (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 5.0.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class CategoricalGenLinModel

java.lang.Object
  com.imsl.stat.CategoricalGenLinModel

public class CategoricalGenLinModel
extends Object
extends Object

Analyzes categorical data using logistic, probit, Poisson, and other linear models.

Reweighted least squares is used to compute (extended) maximum likelihood estimates in some generalized linear models involving categorized data. One of several models, including probit, logistic, Poisson, logarithmic, and negative binomial models, may be fit for input point or interval observations. (In the usual case, only point observations are observed.)

Let

${gamma}_i=w_i+x_i^Tbeta=w_i+eta_i$

be the linear response where

is a design column vector obtained from a row of

is the column vector of coefficients to be estimated, and

is a fixed parameter that may be input in x. When some of the ${gamma}_i$ are infinite at the supremum of the likelihood, then extended maximum likelihood estimates are computed. Extended maximum likelihood are computed as the finite (but nonunique) estimates

that optimize the likelihood containing only the observations with finite ${hat{gamma}}_i$ . These estimates, when combined with the set of indices of the observations such that ${hat{gamma}}_i$ is infinite at the supremum of the likelihood, are called extended maximum estimates. When none of the optimal ${hat{gamma}}_i$ are infinite, extended maximum likelihood estimates are identical to maximum likelihood estimates. Extended maximum likelihood estimation is discussed in more detail by Clarkson and Jennrich (1991). In CategoricalGenLinModel, observations with potentially infinite

${hat{eta}}_i = x_i^That{beta}$

are detected and removed from the likelihood if


  infin

= 0. See below.

The models available in CategoricalGenLinModel are:

Model Name	Parameterization	Response PDF
MODEL0 (Poisson)	$lambda=N times{e^{w+eta}}$	$f(y)=lambda^{y}e^{ -lambda}/y!$
MODEL1 (Negative Binomial)	$theta=frac{e^{w+eta}}{1+e^{w+eta}}$	$f(y)=left(begin{array}{rr}S+y-1\y-1end{array}right)theta^S(1- theta)^y$
MODEL2 (Logarithmic)	$theta= frac{e^{w+eta}}{1+e^{w+eta}}$
MODEL3 (Logistic)	$theta=frac {e^{w +eta}}{1+e^{w+eta}}$	$f(y)=left(begin{array}{rr}N\yend{array}right)theta^y(1-theta )^{N-y}$
MODEL4 (Probit)		$f(y)=left(begin{array}{rr}N\y end{array}right)theta^y(1-theta)^{N-y}$
MODEL5 (Log-log)	$theta=1-e^{- e^{w+eta}}$	$f(y)=left(begin{array} {rr}N\yend{array}right)theta^y(1-theta)^{N-y}$

Here denotes the cumulative normal distribution, N and S are known parameters specified for each observation via column ipar of x, and w is an optional fixed parameter specified for each observation via column ifix of x. (By default N is taken to be 1 for model = 0, 3, 4 and 5 and S is taken to be 1 for model = 1. By default w is taken to be 0.) Since the log-log model (model = 5) probabilities are not symmetric with respect to 0.5, quantitatively, as well as qualitatively, different models result when the definitions of "success" and "failure" are interchanged in this distribution. In this model and all other models involving , is taken to be the probability of a "success."

Note that each row vector in the data matrix can represent a single observation; or, through the use of column ifrq of the matrix x, each vector can represent several observations. Also note that classification variables and their products are easily incorporated into the models via the usual regression-type specifications.

Computational Details

For interval observations, the probability of the observation is computed by summing the probability distribution function over the range of values in the observation interval. For right-interval observations, is computed as a sum based upon the equality . Derivatives are computed similarly. CategoricalGenLinModel allows three types of interval observations. In full interval observations, both the lower and the upper endpoints of the interval must be specified. For right-interval observations, only the lower endpoint need be given while for left-interval observations, only the upper endpoint is given.

The computations proceed as follows:

The input parameters are checked for consistency and validity.
Estimates of the means of the "independent" or design variables are computed. The frequency of the observation in all but binomial distribution model is taken from column ifrq of the data matrix x. In binomial distribution models, the frequency is taken as the product of n = x[i][ipar] and x[i][ifrq]. In all cases these values default to 1. Means are computed as
$bar{x}=frac{Sigma_if_ix_i}{Sigma_if_i}$
If init = 0, initial estimates of the coefficients are obtained (based upon the observation intervals) as multiple regression estimates relating transformed observation probabilities to the observation design vector. For example, in the binomial distribution models, for point observations may be estimated as
and, when model = 3, the linear relationship is given by
while if model = 4,
$left(Phi^{-1}(hat{theta})=xbetaright )$
For bounded interval observations, the midpoint of the interval is used for x[i][irt]. Right-interval observations are not used in obtaining initial estimates when the distribution has unbounded support (since the midpoint of the interval is not defined). When computing initial estimates, standard modifications are made to prevent illegal operations such as division by zero.
Regression estimates are obtained at this point, as well as later, by use of linear regression.
Newton-Raphson iteration for the maximum likelihood estimates is implemented via iteratively reweighted least squares. Let
denote the log of the probability of the i-th observation for coefficients . In the least-squares model, the weight of the i-th observation is taken as the absolute value of the second derivative of
with respect to
(times the frequency of the observation), and the dependent variable is taken as the first derivative with respect to , divided by the square root of the weight times the frequency. The Newton step is given by
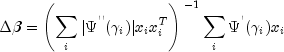
$Deltabeta=left(sum_{i}|Psi^{''}( gamma_i)|x_ix_i^T right)^{-1} sum_{i}Psi^{'}(gamma_i)x_i$
where all derivatives are evaluated at the current estimate of , and $beta_{n+1}=beta_n- Deltabeta$ . This step is computed as the estimated regression coefficients in the least-squares model. Step halving is used when necessary to ensure a decrease in the criterion.
Convergence is assumed when the maximum relative change in any coefficient update from one iteration to the next is less than eps or when the relative change in the log-likelihood from one iteration to the next is less than eps/100. Convergence is also assumed after maxIterations or when step halving leads to a step size of less than .0001 with no increase in the log-likelihood.
For interval observations, the contribution to the log-likelihood is the log of the sum of the probabilities of each possible outcome in the interval. Because the distributions are discrete, the sum may involve many terms. The user should be aware that data with wide intervals can lead to expensive (in terms of computer time) computations.
If setInfiniteEstimateMethod set to 0, then the methods of Clarkson and Jennrich (1991) are used to check for the existence of infinite estimates in
As an example of a situation in which infinite estimates can occur, suppose that observation j is right censored with $t_jgt{15}$ in a logistic model. If design matrix x is is such that $x_{jm}=1$ and $x_{im}=0$ for all , then the optimal estimate of occurs at
$hat{beta_m}=infty$
leading to an infinite estimate of both and . In CategoricalGenLinModel, such estimates may be "computed."
In all models fit by CategoricalGenLinModel, infinite estimates can only occur when the optimal estimated probability associated with the left- or right-censored observation is 1. If setInfiniteEstimateMethod set to 0, left- or right- censored observations that have estimated probability greater than 0.995 at some point during the iterations are excluded from the log-likelihood, and the iterations proceed with a log-likelihood based upon the remaining observations. This allows convergence of the algorithm when the maximum relative change in the estimated coefficients is small and also allows for the determination of observations with infinite
At convergence, linear programming is used to ensure that the eliminated observations have infinite . If some (or all) of the removed observations should not have been removed (because their estimated $eta_{i's}$ must be finite), then the iterations are restarted with a log-likelihood based upon the finite observations. See Clarkson and Jennrich (1991) for more details.

When setInfiniteEstimateMethod is set to 1, no observations are eliminated during the iterations. In this case, when infinite estimates occur, some (or all) of the coefficient estimates will become large, and it is likely that the Hessian will become (numerically) singular prior to convergence.

When infinite estimates for the $hat{eta_i}$ are detected, linear regression (see Chapter 2, Regression;) is used at the convergence of the algorithm to obtain unique estimates . This is accomplished by regressing the optimal $hat{eta_i}$ or the observations with finite against , yielding a unique (by setting coefficients that are linearly related to previous coefficients in the model to zero). All of the final statistics relating to are based upon these estimates.
Residuals are computed according to methods discussed by Pregibon (1981). Let denote the log-likelihood of the i-th observation evaluated at . Then, the standardized residual is computed as
$r_i=frac{ell_i^{'}(hat{gamma_i})}{ sqrt{ell_i^{''}(hat{gamma_i})}}$
where $hat{gamma_i}$ is the value of when evaluated at the optimal and the derivatives here (and only here) are with respect to rather than with respect to . The denominator of this expression is used as the "standard error of the residual" while the numerator is the "raw" residual.
Following Cook and Weisberg (1982), we take the influence of the i-th observation to be
$ell_i^{'}(hat{gamma_i})^Tell^{''}(hat {gamma})^{-1}ell^{'}(hat{gamma_i})$
This quantity is a one-step approximation to the change in the estimates when the i-th observation is deleted. Here, the partial derivatives are with respect to .

Programming Notes

Classification variables are specified via setClassificationVariableColumn. Indicator or dummy variables are created for the classification variables.
To enhance precision "centering" of covariates is performed if setModelIntercept is set to 1 and (number of observations) - (number of rows in x missing one or more values) > 1. In doing so, the sample means of the design variables are subtracted from each observation prior to its inclusion in the model. On convergence the intercept, its variance and its covariance with the remaining estimates are transformed to the uncentered estimate values.
Two methods for specifying a binomial distribution model are possible. In the first method, x[i][ifrq] contains the frequency of the observation while x[i][irt] is 0 or 1 depending upon whether the observation is a success or failure. In this case, N = x[i][ipar] is always 1. The model is treated as repeated Bernoulli trials, and interval observations are not possible.

A second method for specifying binomial models is to use x[i][irt] to represent the number of successes in the x[i][ipar] trials. In this case, x[i][ifrq] will usually be 1, but it may be greater than 1, in which case interval observations are possible.

Note that the solve method must be called prior to calling the "get" member functions, otherwise a null is returned.

See Also:: Example 1, Example 2

Nested Class Summary
`static class`	`CategoricalGenLinModel.ClassificationVariableException` The ClassificationVariable vector has not been initialized.
`static class`	`CategoricalGenLinModel.ClassificationVariableLimitException` The Classification Variable limit set by the user through `setUpperBound` has been exceeded.
`static class`	`CategoricalGenLinModel.ClassificationVariableValueException` The number of distinct values for each Classification Variable must be greater than 1.
`static class`	`CategoricalGenLinModel.DeleteObservationsException` The number of observations to be deleted (set by `setObservationMax`) has grown too large.

Field Summary
`static int`	`MODEL0` Indicates an exponential function is used to model the distribution parameter.
`static int`	`MODEL1` Indicates a logistic function is used to model the distribution parameter.
`static int`	`MODEL2` Indicates a logistic function is used to model the distribution parameter.
`static int`	`MODEL3` Indicates a logistic function is used to model the distribution parameter.
`static int`	`MODEL4` Indicates a probit function is used to model the distribution parameter.
`static int`	`MODEL5` Indicates a log-log function is used to model the distribution parameter.

Constructor Summary
`CategoricalGenLinModel(double[][] x, int model)` Constructs a new `CategoricalGenLinModel`.

Method Summary
`double[][]`	`getCaseAnalysis()` Returns the case analysis.
`int[]`	`getClassificationVariableCounts()` Returns the number of values taken by each classification variable.
`double[]`	`getClassificationVariableValues()` Returns the distinct values of the classification variables in ascending order.
`double[][]`	`getCovarianceMatrix()` Returns the estimated asymptotic covariance matrix of the coefficients.
`double[]`	`getDesignVariableMeans()` Returns the means of the design variables.
`int[]`	`getExtendedLikelihoodObservations()` Returns a vector indicating which observations are included in the extended likelihood.
`double[][]`	`getHessian()` Returns the Hessian computed at the initial parameter estimates.
`double[]`	`getLastParameterUpdates()` Returns the last parameter updates (excluding step halvings).
`int`	`getNRowsMissing()` Returns the number of rows of data in `x` that contain missing values in one or more specific columns of `x`.
`double`	`getOptimizedCriterion()` Returns the optimized criterion.
`double[][]`	`getParameters()` Returns the parameter estimates and associated statistics.
`double[]`	`getProduct()` Returns the inverse of the Hessian times the gradient vector computed at the input parameter estimates.
`void`	`setCensorColumn(int icen)` Sets the column number in `x` which contains the interval type for each observation.
`void`	`setClassificationVariableColumn(int[] indcl)` Initializes an index vector to contain the column numbers in `x` that are classification variables.
`void`	`setConvergenceTolerance(double eps)` Set the convergence criterion.
`void`	`setEffects(int[] indef, int[] nvef)` Initializes an index vector to contain the column numbers in `x` associated with each effect.
`void`	`setExtendedLikelihoodObservations(int[] iadds)` Initializes a vector indicating which observations are to be included in the extended likelihood.
`void`	`setFixedParameterColumn(int ifix)` Sets the column number in `x` that contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter.
`void`	`setFrequencyColumn(int ifrq)` Sets the column number in `x` that contains the frequency of response for each observation.
`void`	`setInfiniteEstimateMethod(int infin)` Sets the method to be used for handling infinite estimates.
`void`	`setInitialEstimates(int init, double[] estimates)` Sets the initial parameter estimates option.
`void`	`setLowerEndpointColumn(int irt)` Sets the column number in `x` that contains the lower endpoint of the observation interval for full interval and right interval observations.
`void`	`setMaxIterations(int maxIterations)` Set the maximum number of iterations allowed.
`void`	`setModelIntercept(int intcep)` Sets the intercept option.
`void`	`setObservationMax(int nmax)` Sets the maximum number of observations that can be handled in the linear programming.
`void`	`setOptionalDistributionParameterColumn(int ipar)` Sets the column number in `x` that contains an optional distribution parameter for each observation.
`void`	`setUpperBound(int maxcl)` Sets the upper bound on the sum of the number of distinct values taken on by each classification variable.
`void`	`setUpperEndpointColumn(int ilt)` Sets the column number in `x` that contains the upper endpoint of the observation interval for full interval and left interval observations.
`double[][]`	`solve()` Returns the parameter estimates and associated statistics for a CategoricalGenLinModel object.

Methods inherited from class java.lang.Object
`clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait`

Field Detail

MODEL0

public static final int MODEL0

Indicates an exponential function is used to model the distribution parameter. The distribution of the response variable is Poisson. The lower bound of the response variable is 0.

See Also:: Constant Field Values

MODEL1

public static final int MODEL1

Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is negative Binomial. The lower bound of the response variable is 0.

See Also:: Constant Field Values

MODEL2

public static final int MODEL2

Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is Logarithmic. The lower bound of the response variable is 1.

See Also:: Constant Field Values

MODEL3

public static final int MODEL3

Indicates a logistic function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.

See Also:: Constant Field Values

MODEL4

public static final int MODEL4

Indicates a probit function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.

See Also:: Constant Field Values

MODEL5

public static final int MODEL5

Indicates a log-log function is used to model the distribution parameter. The distribution of the response variable is Binomial. The lower bound of the response variable is 0.

See Also:: Constant Field Values

Constructor Detail

CategoricalGenLinModel

public CategoricalGenLinModel(double[][] x,
                              int model)

Constructs a new CategoricalGenLinModel.

Parameters:

x - A double input matrix containing the data where the number of rows in the matrix is equal to the number of observations.

model - An int scalar which specifies the distribution of the response variable and the function used to model the distribution parameter. Use one of the class members from the following table. The lower bound given in the table is the minimum possible value of the response variable:

Model	Distribution	Function	Lower-bound
0	Poisson	Exponential	0
1	Negative Binomial	Logistic	0
2	Logarithmic	Logistic	1
3	Binomial	Logistic	0
4	Binomial	Probit	0
5	Binomial	Log-log	0

Let

be the dot product of a row in the design matrix with the parameters (plus the fixed parameter, if used). Then, the functions used to model the distribution parameter are given by:

Name	Function
Exponential	$e^{gamma}$
Logistic	$e^{gamma}/({1 + e^{gamma}})$
Probit	(where is the normal cdf)
Log-log	$1- e^{-gamma}$

Method Detail

getCaseAnalysis

public double[][] getCaseAnalysis()

Returns the case analysis.

Returns:

A double matrix containing the case analysis or null if solve has not been called. The matrix is

where nobs is the number of observations. The matrix contains:

Column	Statistic
0	Prediction.
1	The residual.
2	The estimated standard error of the residual.
3	The estimated influence of the observation.
4	The standardized residual.

Case studies are computed for all observations except where missing values prevent their computation. The prediction in column 0 depends upon the model used as follows:

Model	Prediction
0	The predicted mean for the observation.
1-4	The probability of a success on a single trial.

getClassificationVariableCounts

public int[] getClassificationVariableCounts()
                                      throws CategoricalGenLinModel.ClassificationVariableException

Returns the number of values taken by each classification variable.

Returns:: An int array of length nclvar containing the number of values taken by each classification variable where nclvar is the number of classification variables or null if solve has not been called.
Throws:: CategoricalGenLinModel.ClassificationVariableException - is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1

getClassificationVariableValues

public double[] getClassificationVariableValues()
                                         throws CategoricalGenLinModel.ClassificationVariableException

Returns the distinct values of the classification variables in ascending order.

Returns:: A double array of length $sum_{k=0}^{ mbox{nclvar}}mbox{nclval[k]}$ containing the distinct values of the classification variables in ascending order where nclvar is the number of classification variables and nclval[i] is the number of values taken by the i-th classification variable. A null is returned if solve has not been called prior to calling this method.
Throws:: CategoricalGenLinModel.ClassificationVariableException - is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1

getCovarianceMatrix

public double[][] getCovarianceMatrix()

Returns the estimated asymptotic covariance matrix of the coefficients.

Returns:: A double matrix containing the estimated asymptotic covariance matrix of the coefficients or null if solve has not been called. The covariance matrix is nCoef by nCoef where nCoef is the number of coefficients in the model.

getDesignVariableMeans

public double[] getDesignVariableMeans()

Returns the means of the design variables.

Returns:: A double array of length nCoef containing the means of the design variables where nCoef is the number of coefficients in the model or null if solve has not been called.

getExtendedLikelihoodObservations

public int[] getExtendedLikelihoodObservations()

Returns a vector indicating which observations are included in the extended likelihood.

Returns:

An int array of length nobs indicating which observations are included in the extended likelihood where nobs is the number of observations. The values within the array are interpreted as:

Value	Status of observation
0	Observation i is in the likelihood.
1	Observation i cannot be in the likelihood because it contains at least one missing value in `x`.
2	Observation i is not in the likelihood. Its estimated parameter is infinite.

A null is returned if solve has not been called prior to calling this method.

getHessian

public double[][] getHessian()
                      throws CategoricalGenLinModel.ClassificationVariableException,
                             CategoricalGenLinModel.ClassificationVariableLimitException,
                             CategoricalGenLinModel.ClassificationVariableValueException,
                             CategoricalGenLinModel.DeleteObservationsException

Returns the Hessian computed at the initial parameter estimates.

Returns:: A double matrix containing the Hessian computed at the input parameter estimates. The Hessian matrix is nCoef by nCoef where nCoef is the number of coefficients in the model. This member function will call solve to get the Hessian if the Hessian has not already been computed.
Throws:: CategoricalGenLinModel.ClassificationVariableException - is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1; CategoricalGenLinModel.ClassificationVariableLimitException - is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed, maxcl; CategoricalGenLinModel.DeleteObservationsException - is thrown if the number of observations to be deleted has grown too large; CategoricalGenLinModel.ClassificationVariableValueException

getLastParameterUpdates

public double[] getLastParameterUpdates()

Returns the last parameter updates (excluding step halvings).

Returns:: A double array of length nCoef containing the last parameter updates (excluding step halvings) or null if solve has not been called.

getNRowsMissing

public int getNRowsMissing()

Returns the number of rows of data in x that contain missing values in one or more specific columns of x.

Returns:: An int scalar representing the number of rows of data in x that contain missing values in one or more specific columns of x or null if solve has not been called. The columns of x included in the count are the columns containing the upper or lower endpoints of full interval, left interval, or right interval observations. Also included are the columns containing the frequency responses, fixed parameters, optional distribution parameters, and interval type for each observation. Columns containing classification variables and columns associated with each effect in the model are also included.

getOptimizedCriterion

public double getOptimizedCriterion()

Returns the optimized criterion.

Returns:: A double scalar representing the optimized criterion or null if solve has not been called. The criterion to be maximized is a constant plus the log-likelihood.

getParameters

public double[][] getParameters()

Returns the parameter estimates and associated statistics.

Returns:

An nCoef row by 4 column double matrix containing the parameter estimates and associated statistics or null if solve has not been called. Here, nCoef is the number of coefficients in the model. The statistics returned are as follows:

Column	Statistic
0	Coefficient estimate.
1	Estimated standard deviation of the estimated coefficient.
2	Asymptotic normal score for testing that the coefficient is zero.
3	- value associated with the normal score in column 2.

getProduct

public double[] getProduct()
                    throws CategoricalGenLinModel.ClassificationVariableException,
                           CategoricalGenLinModel.ClassificationVariableLimitException,
                           CategoricalGenLinModel.ClassificationVariableValueException,
                           CategoricalGenLinModel.DeleteObservationsException

Returns the inverse of the Hessian times the gradient vector computed at the input parameter estimates.

Returns:: A double array of length nCoef containing the inverse of the Hessian times the gradient vector computed at the input parameter estimates. nCoef is the number of coefficients in the model. This member function will call solve to get the product if the product has not already been computed.
Throws:: CategoricalGenLinModel.ClassificationVariableException - is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1; CategoricalGenLinModel.ClassificationVariableLimitException - is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed, maxcl; CategoricalGenLinModel.DeleteObservationsException - is thrown if the number of observations to be deleted has grown too large; CategoricalGenLinModel.ClassificationVariableValueException

setCensorColumn

public void setCensorColumn(int icen)

Sets the column number in x which contains the interval type for each observation.

Parameters:

icen - An int scalar which indicates the column number x which contains the interval type code for each observation. The valid codes are interpreted as:

`x[i][icen]`	Censoring
0	Point observation. The response is unique and is given by `x[i][irt]`.
1	Right interval. The response is greater than or equal to `x[i][irt]` and less than or equal to the upper bound, if any, of the distribution.
2	Left interval. The response is less than or equal to `x[i][ilt]` and greater than or equal to the lower bound of the distribution.
3	Full interval. The response is greater than or equal to `x[i][irt]` but less than or equal to `x[i][ilt].`

If this member function is not called a censoring code of 0 is assumed.

Throws:

IllegalArgumentException - is thrown when icen is less than 0 or greater than or equal to the number of columns of x

setClassificationVariableColumn

public void setClassificationVariableColumn(int[] indcl)

Initializes an index vector to contain the column numbers in

that are classification variables.

Parameters:: indcl - An int vector which contains the column numbers in x that are classification variables. By default this vector is not referenced.
Throws:: IllegalArgumentException - is thrown when an element of indcl is less than 0 or greater than or equal to the number of columns of x

setConvergenceTolerance

public void setConvergenceTolerance(double eps)

Set the convergence criterion.

Parameters:: eps - A double scalar specifying the convergence criterion. Convergence is assumed when the maximum relative change in any coefficient estimate is less than eps from one iteration to the next or when the relative change in the log-likelihood, getOptimizedCriterion, from one iteration to the next is less than eps/100. eps must be greater than 0. If this member function is not called, eps = .001 is assumed.
Throws:: IllegalArgumentException - is thrown if eps is or equal to 0

setEffects

public void setEffects(int[] indef,
                       int[] nvef)

Initializes an index vector to contain the column numbers in

associated with each effect.

Parameters:: indef - An int vector of length $sum_{k=0}^{mbox{nef}-1}mbox{nvef[k]}$ where nef is the number of effects in the model. indef contains the column numbers in x that are associated with each effect. Member function setEffects(int [], nvef []) sets the number of variables associated with each effect in the model. The first nvef[0] elements of indef give the column numbers of the variables in the first effect. The next nvef[0] elements give the column numbers of the variables in the second effect, etc. By default this vector is not referenced.; nvef - An int vector of length nef where nef is the number of effects in the model. nvef contains the number of variables associated with each effect in the model. By default this vector is not referenced.
Throws:: IllegalArgumentException - is thrown when an element of indef is less than 0 or greater than or equal to the number of columns of x or if an element of nvef is less than or equal to 0

setExtendedLikelihoodObservations

public void setExtendedLikelihoodObservations(int[] iadds)

Initializes a vector indicating which observations are to be included in the extended likelihood.

Parameters:

iadds - An int array of length nobs indicating which observations are included in the extended likelihood where nobs is the number of observations. The values within the array are interpreted as:

Value	Status of observation
0	Observation i is in the likelihood.
1	Observation i cannot be in the likelihood because it contains at least one missing value in `x`.
2	Observation i is not in the likelihood. Its estimated parameter is infinite.

If this member function is not called,

iadds

is set to all zeroes.

Throws:

IllegalArgumentException - is thrown when an element of iadds is not in the range [0,2]

setFixedParameterColumn

public void setFixedParameterColumn(int ifix)

Sets the column number in x that contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter.

Parameters:: ifix - An int scalar which indicates the column number in x that contains a fixed parameter for each observation that is added to the linear response prior to computing the model parameter. The "fixed" parameter allows one to test hypothesis about the parameters via the log-likelihoods. By default the fixed parameter is assumed to be zero.
Throws:: IllegalArgumentException - is thrown when ifix is less than 0 or greater than or equal to the number of columns of x

setFrequencyColumn

public void setFrequencyColumn(int ifrq)

Sets the column number in x that contains the frequency of response for each observation.

Parameters:: ifrq - An int scalar which indicates the column number in x that contains the frequency of response for each observation. By default a frequency of 1 for each observation is assumed.
Throws:: IllegalArgumentException - is thrown when ifrq is less than 0 or greater than or equal to the number of columns of x

setInfiniteEstimateMethod

public void setInfiniteEstimateMethod(int infin)

Sets the method to be used for handling infinite estimates.

Parameters:

infin - An int scalar which indicates the method to be used for handling infinite estimates. The method value is interpreted as follows:

`infin`	Method
0	Remove a right or left-censored observation from the log-likelihood whenever the probability of the observation exceeds 0.995. At convergence, use linear programming to check that all removed observations actually have an estimated linear response that is infinite. Set `iadds[i]` for observation i to 2 if the linear response is infinite. If not all removed observations have infinite linear response, recompute the estimates based upon the observations with estimated linear response that is finite. This option is valid only for censoring codes 1 and 2.
1	Iterate without checking for infinite estimates.

By default infin = 1.

Throws:

IllegalArgumentException - is thrown when

infin

is less than 0 or greater than 1

setInitialEstimates

public void setInitialEstimates(int init,
                                double[] estimates)

Sets the initial parameter estimates option.

Parameters:

init - An input int indicating the desired initialization method for the initial estimates of the parameters. If this method is not called,

init

is set to 0.

`init`	Action
0	Unweighted linear regression is used to obtain initial estimates.
1	The nCoef, number of coefficients, elements of `estimates` contain initial estimates of the parameters. Use of this option requires that the user know nCoef beforehand.

estimates - An input double array of length nCoef containing the initial estimates of the parameters where nCoef is the number of estimated coefficients in the model. (Used if


                      init

= 1.) If this member function is not called, unweighted linear regression is used to obtain the initial estimates.

Throws:

IllegalArgumentException - is thrown when init is not in the range [0,1]

setLowerEndpointColumn

public void setLowerEndpointColumn(int irt)

Sets the column number in x that contains the lower endpoint of the observation interval for full interval and right interval observations.

Parameters:: irt - An int scalar which indicates the column number in x that contains the lower endpoint of the observation interval for full interval and right interval observations. By default all observations are treated as "point" observations and x[i][irt] contains the observation point. If this member function is not called, the last column of x is assumed to contain the "point" observations.
Throws:: IllegalArgumentException - is thrown when irt is less than 0 or greater than or equal to the number of columns of x

setMaxIterations

public void setMaxIterations(int maxIterations)

Set the maximum number of iterations allowed.

Parameters:: maxIterations - An int specifying the maximum number of iterations allowed. maxIterations must be greater than 0. If this member function is not called, the maximum number of iterations is set to 30.
Throws:: IllegalArgumentException - is thrown if maxIterations is less than or equal to 0

setModelIntercept

public void setModelIntercept(int intcep)

Sets the intercept option.

Parameters:

intcep - An int scalar which indicates whether or not the model has an intercept. Input

intcep

is interpreted as follows:

Value	Action
0	No intercept is in the model (unless otherwise provided for by the user).
1	Intercept is automatically included in the model.

By default intcep = 1.

Throws:

IllegalArgumentException - is thrown when intcep is less than 0 or greater than 1

setObservationMax

public void setObservationMax(int nmax)

Sets the maximum number of observations that can be handled in the linear programming.

Parameters:: nmax - An int scalar which sets the maximum number of observations that can be handled in the linear programming. An illegal argument exception is thrown if nmax is less than 0. If this member function is not called, nmax is set to the number of observations.
Throws:: IllegalArgumentException - is thrown when nmax is less than 0

setOptionalDistributionParameterColumn

public void setOptionalDistributionParameterColumn(int ipar)

Sets the column number in x that contains an optional distribution parameter for each observation.

Parameters:

ipar - An int scalar which indicates the column number in x that contains an optional distribution parameter for each observation. The distribution parameter values are interpreted as follows depending on the model chosen:

Model	Meaning of `x[i][ipar]`
0	The Poisson parameter is given by $x[i][ipar]times {e^rho}$ .
1	The number of successes required in the negative binomial is given by `x[i][ipar].`
2	`x[i][ipar] is not used.`
3-5	The number of trials in the binomial distribution is given by `x[i][ipar].`

By default the distribution parameter is assumed to be 1.

Throws:

IllegalArgumentException - is thrown when ipar is less than 0 or greater than or equal to the number of columns of x

setUpperBound

public void setUpperBound(int maxcl)

Sets the upper bound on the sum of the number of distinct values taken on by each classification variable.

Parameters:: maxcl - An int scalar specifying the upper bound on the sum of the number of distinct values taken on by each classification variable. If this member function is not called, an upper bound of 1 is used if method setClassificationVariableColumn has not been referenced. Otherwise, the default upper bound is set to nobs * nclvar where nobs is the number of observations and nclvar is the number of classification variables.
Throws:: IllegalArgumentException - is thrown when maxcl is less than 1 and the number of classification variables is greater than 0

setUpperEndpointColumn

public void setUpperEndpointColumn(int ilt)

Sets the column number in x that contains the upper endpoint of the observation interval for full interval and left interval observations.

Parameters:: ilt - An int scalar which indicates the column number in x that contains the upper endpoint of the observation interval for full interval and left interval observations. By default all observations are treated as "point" observations.
Throws:: IllegalArgumentException - is thrown when ilt is less than 0 or greater than or equal to the number of columns of x

solve

public double[][] solve()
                 throws CategoricalGenLinModel.ClassificationVariableException,
                        CategoricalGenLinModel.ClassificationVariableLimitException,
                        CategoricalGenLinModel.ClassificationVariableValueException,
                        CategoricalGenLinModel.DeleteObservationsException

Returns the parameter estimates and associated statistics for a CategoricalGenLinModel object.

Returns:

An nCoef row by 4 column double matrix containing the parameter estimates and associated statistics. Here, nCoef is the number of coefficients in the model. The statistics returned are as follows:

Column	Statistic
0	Coefficient estimate.
1	Estimated standard deviation of the estimated coefficient.
2	Asymptotic normal score for testing that the coefficient is zero.
3	- value associated with the normal score in column 2.

Throws:

CategoricalGenLinModel.ClassificationVariableException - is thrown when the number of values taken by each classification variable has been set by the user to be less than or equal to 1

CategoricalGenLinModel.ClassificationVariableLimitException - is thrown when the sum of the number of distinct values taken on by each classification variable exceeds the maximum allowed, maxcl

CategoricalGenLinModel.DeleteObservationsException - is thrown if the number of observations to be deleted has grown too large

CategoricalGenLinModel.ClassificationVariableValueException

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 5.0.1

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat Class CategoricalGenLinModel

Computational Details

Programming Notes

MODEL0

MODEL1

MODEL2

MODEL3

MODEL4

MODEL5

CategoricalGenLinModel

getCaseAnalysis

getClassificationVariableCounts

getClassificationVariableValues

getCovarianceMatrix

getDesignVariableMeans

getExtendedLikelihoodObservations

getHessian

getLastParameterUpdates

getNRowsMissing

getOptimizedCriterion

getParameters

getProduct

setCensorColumn

setClassificationVariableColumn

setConvergenceTolerance

setEffects

setExtendedLikelihoodObservations

setFixedParameterColumn

setFrequencyColumn

setInfiniteEstimateMethod

setInitialEstimates

setLowerEndpointColumn

setMaxIterations

setModelIntercept

setObservationMax

setOptionalDistributionParameterColumn

setUpperBound

setUpperEndpointColumn

solve

com.imsl.stat
Class CategoricalGenLinModel