JMSL Chart Guide: EWMA

JMSL Chart Programmer's Guide

Quality Control and Improvement Charts >> EWMA

EWMA

EWMA is the exponentially weighted moving average control chart. It is very effective in detecting small process shifts, but is slower than Shewhart charts at detecting large process shifts.

The exponentially weighted moving average is defined to be

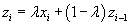
where 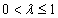is a constant and the starting value is 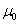, the expected mean.

The control limits in EWMA are defined by the equations:

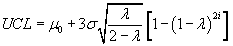
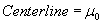
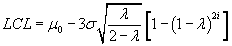
Where 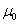is the historical mean, 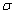is the historical standard deviation, and i is the sample number. Because of the presence of i the control limits are stair steps, not constants.

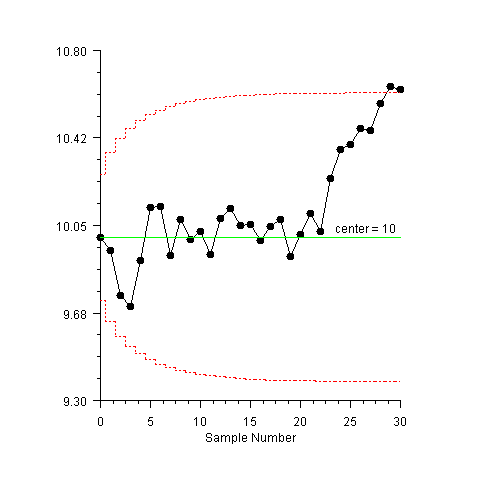
EWMA Example

The expected mean is 10., the expected standard deviation is 1.0 and 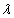is 0.10. Also, the control limit values are 2.7, not the default value of 3 (Montgomery 428).

(Download Code)

import com.imsl.chart.*;
import com.imsl.chart.qc.*;

public class SampleEWMA extends JFrameChart {      
    static final double data[] = {
        9.45, 7.99, 9.29, 11.66, 12.16, 10.18, 8.04, 11.46, 9.20, 10.34, 9.03, 
        11.47, 10.51, 9.40, 10.08, 9.37, 10.62, 10.31, 8.52, 10.84, 10.90, 
        9.33, 12.29, 11.50, 10.60, 11.08, 10.38, 11.62, 11.31, 10.52
    };
    
    public SampleEWMA() {
        Chart chart = getChart();
        AxisXY axis = new AxisXY(chart);
        double lambda = 0.10;
        double mean = 10.0;
        double stdev = 1.0;
        EWMA ewma = new EWMA(axis, data, lambda, mean, stdev);
        ewma.getLowerControlLimit().setControlLimit(-2.7);
        ewma.getUpperControlLimit().setControlLimit(2.7);
        
        axis.getAxisX().getAxisTitle().setTitle("Sample Number");
        axis.getAxisX().getAxisLabel().setTextFormat("0");
        axis.getAxisY().setWindow(9.3, 10.8);
        axis.getAxisY().setAutoscaleInput(0);
    }
        
    public static void main(String argv[]) {
        new SampleEWMA().setVisible(true);
    }
}