- java.lang.Object
-
- com.imsl.finance.Bond
-
public class Bond extends Object
Collection of bond functions.Definitions
rate is an annualized rate of return based on the par value of the bills.
yield is an annualized rate based on the purchase price and reflects the actual yield to maturity.
coupons are interest payments on a bond.
redemption is the amount a bond pays at maturity.
frequency is the number of times a year that a bond makes interest payments.
basis is the method used to calculate dates. For example, sometimes computations are done assuming 360 days in a year.
issue is the day a bond is first sold.
settlement is the day a purchaser acquires a bond.
maturity is the day a bond's principal is repaid.
Discount Bonds
Discount bonds, also called zero-coupon bonds, do not pay interest during the life of the security, instead they sell at a discount to their value at maturity. The discount bond methods all have settlement, maturity, basis, and redemption as arguments. In the following list these common arguments are omitted.- price =
pricedisc(rate) - price =
priceyield(yield) - price =
pricemat(issue, rate, yield) - rate =
disc(price) - yield =
yielddisc(price)
accrintm, which returns the interest that has accumulated on the discount bond.Treasury Bills
US Treasury bills are a special case of discount bonds. The basis is fixed for treasury bills and the redemption value is assumed to be $100. So these functions have only settlement and maturity as common arguments.- price =
tbillprice(rate) - yield =
tbillyield(price) - yield =
tbilleq(rate)
Interest-Paying Bonds
Most bonds pay interest periodically. The interest-paying bond methods all have settlement, maturity, basis, and frequency as arguments. Again suppressing the common arguments,- price =
price(rate, yield, redemption) - yield =
yield(rate, price, redemption) - redemption =
received(price, rate)
accrint, which returns the interest that has accumulated at settlement from the previous coupon date.Interest-Paying Bonds with Odd Coupon Periods
An odd coupon period is one that is either shorter or longer than the regular coupon period. Odd coupon periods typically occur in the first or the last payment period. The yield and price functions accept two additional arguments in order to make the proper adjustments for odd coupon periods:issueDateandfirstCouponDateorlastCouponDate.- oddFirstPrice =
price(settlement, maturity, issueDate, firstCouponDate, rate, yield, redemption, frequency, basis) - oddLastPrice =
price(settlement, maturity, lastCouponDate, rate, yield, redemption, frequency, basis) - oddFirstYield =
yield(settlement, maturity, issueDate, firstCouponDate, rate, price, redemption, frequency, basis) - oddLastYield =
yield(settlement, maturity, lastCouponDate, rate, price, redemption, frequency, basis)
Coupon days
In this diagram, the settlement date is shown as a hollow circle and the adjacent coupon dates are shown as filled circles.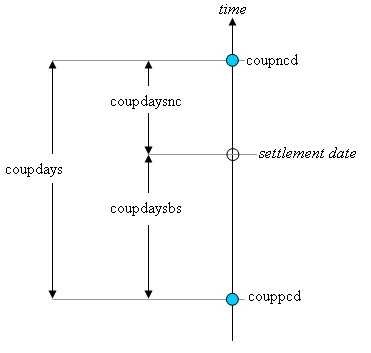
coupppcdis the coupon date immediately prior to the settlement date.coupncdis the coupon date immediately after the settlement date.coupdaybsis the number of days from the immediately prior coupon date to the settlement date.coupdaysncis the number of days from the settlement date to the next coupon date.coupdaysis the number of days between these two coupon dates.
coupnum, which returns the number of coupons payable between settlement and maturity.Another related method is
yearfrac, which returns the fraction of the year between two days.Duration
Duration is used to measure the sensitivity of a bond to changes in interest rates. Convexity is a measure of the sensitivity of duration. - price =
-
-
Field Summary
Fields Modifier and Type Field and Description static intANNUALCoupon payments are made annually.static intBIMONTHLYCoupon payments are made bimonthly (6 times per year).static intMONTHLYCoupon payments are made monthly.static intQUARTERLYCoupon payments are made quarterly.static intSEMIANNUALCoupon payments are made semiannually (twice per year).
-
Method Summary
Methods Modifier and Type Method and Description static doubleaccrint(GregorianCalendar issue, GregorianCalendar firstCoupon, GregorianCalendar settlement, double rate, double par, int frequency, DayCountBasis basis)Returns the interest which has accrued on a security that pays interest periodically.static doubleaccrintm(GregorianCalendar issue, GregorianCalendar maturity, double rate, double par, DayCountBasis basis)Returns the interest which has accrued on a security that pays interest at maturity.static doubleamordegrc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)Returns the depreciation for each accounting period.static doubleamorlinc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)Returns the depreciation for each accounting period.static doubleconvexity(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)Returns the convexity for a security.static intcoupdaybs(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the number of days starting with the beginning of the coupon period and ending with the settlement date.static doublecoupdays(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the number of days in the coupon period containing the settlement date.static intcoupdaysnc(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the number of days starting with the settlement date and ending with the next coupon date.static GregorianCalendarcoupncd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the first coupon date which follows the settlement date.static intcoupnum(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the number of coupons payable between the settlement date and the maturity date.static GregorianCalendarcouppcd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)Returns the coupon date which immediately precedes the settlement date.static doubledisc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)Returns the implied interest rate of a discount bond.static doubleduration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)Returns the Macaulay duration of a security where the security has periodic interest payments.static doubleintrate(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double redemption, DayCountBasis basis)Returns the interest rate of a fully invested security.static doublemduration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)Returns the modified Macaulay duration for a security with an assumed par value of $100.static doubleprice(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double yield, double redemption, int frequency, DayCountBasis basis)Returns the price, per $100 face value, of a security that pays periodic interest.static doubleprice(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)Returns the price of an odd last period coupon bond, given its yield.static doubleprice(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)Returns the price of an odd first period, coupon bond, given its yield.static doublepricedisc(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double redemption, DayCountBasis basis)Returns the price of a discount bond given the discount rate.static doublepricemat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double yield, DayCountBasis basis)Returns the price, per $100 face value, of a discount bond.static doublepriceyield(GregorianCalendar settlement, GregorianCalendar maturity, double yield, double redemption, DayCountBasis basis)Returns the price of a discount bond given the yield.static doublereceived(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double rate, DayCountBasis basis)Returns the amount one receives when a fully invested security reaches the maturity date.static doubletbilleq(GregorianCalendar settlement, GregorianCalendar maturity, double rate)Returns the bond-equivalent yield of a Treasury bill.static doubletbillprice(GregorianCalendar settlement, GregorianCalendar maturity, double rate)Returns the price, per $100 face value, of a Treasury bill.static doubletbillyield(GregorianCalendar settlement, GregorianCalendar maturity, double price)Returns the yield of a Treasury bill.static doubleyearfrac(GregorianCalendar start, GregorianCalendar end, DayCountBasis basis)Returns the fraction of a year represented by the number of whole days between two dates.static doubleyield(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double price, double redemption, int frequency, DayCountBasis basis)Returns the yield of a security that pays periodic interest.static doubleyield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)Returns the yield of a security with an odd last coupon period that pays periodic interest.static doubleyield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)Returns the yield of a security with an odd first coupon period that pays periodic interest.static doubleyielddisc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)Returns the annual yield of a discount bond.static doubleyieldmat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double price, DayCountBasis basis)Returns the annual yield of a security that pays interest at maturity.
-
-
-
Field Detail
-
ANNUAL
public static final int ANNUAL
Coupon payments are made annually.- See Also:
- Constant Field Values
-
BIMONTHLY
public static final int BIMONTHLY
Coupon payments are made bimonthly (6 times per year).- See Also:
- Constant Field Values
-
MONTHLY
public static final int MONTHLY
Coupon payments are made monthly.- See Also:
- Constant Field Values
-
QUARTERLY
public static final int QUARTERLY
Coupon payments are made quarterly.- See Also:
- Constant Field Values
-
SEMIANNUAL
public static final int SEMIANNUAL
Coupon payments are made semiannually (twice per year).- See Also:
- Constant Field Values
-
-
Method Detail
-
accrint
public static double accrint(GregorianCalendar issue, GregorianCalendar firstCoupon, GregorianCalendar settlement, double rate, double par, int frequency, DayCountBasis basis)
Returns the interest which has accrued on a security that pays interest periodically. In the equation below, Ai represents the number of days which have accrued for the ith quasi-coupon period within the odd period. The quasi-coupon periods are periods obtained by extending the series of equal payment periods to before or after the actual payment periods. NC represents the number of quasi-coupon periods within the odd period, rounded to the next highest integer. NLi represents the length of the normal ith quasi-coupon period within the odd period. NLi is expressed in days. Functionaccrintcan be found by solving the following: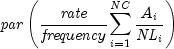
- Parameters:
issue- aGregorianCalendarissue date of the securityfirstCoupon- aGregorianCalendardate of the security's first interest datesettlement- aGregorianCalendarsettlement date of the securityrate- adoublewhich specifies the security's annual coupon ratepar- adoublewhich specifies the security's par valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the accrued interest - See Also:
- Example
-
accrintm
public static double accrintm(GregorianCalendar issue, GregorianCalendar maturity, double rate, double par, DayCountBasis basis)
Returns the interest which has accrued on a security that pays interest at maturity.
In the above equation,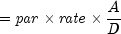
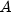 represents the number of
days starting at issue date to maturity date and
represents the number of
days starting at issue date to maturity date and 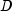 represents the annual basis.
represents the annual basis.- Parameters:
issue- aGregorianCalendarissue date of the securitymaturity- aGregorianCalendardate of the security's maturityrate- adoublewhich specifies the security's annual coupon ratepar- adoublewhich specifies the security's par valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the accrued interest - See Also:
- Example
-
amordegrc
public static double amordegrc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)Returns the depreciation for each accounting period. This method is similar toamorlinc. However, in this method a depreciation coefficient based on the asset life is applied during the evaluation of the function.- Parameters:
cost- adoublewhich specifies the cost of the assetissue- aGregorianCalendarissue date of the assetfirstPeriod- aGregorianCalendardate of the end of the first periodsalvage- adoublewhich specifies the asset's salvage value at the end of the life of the assetperiod- anintwhich specifies the periodrate- adoublewhich specifies the rate of depreciationbasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the depreciation - See Also:
- Example
-
amorlinc
public static double amorlinc(double cost, GregorianCalendar issue, GregorianCalendar firstPeriod, double salvage, int period, double rate, DayCountBasis basis)Returns the depreciation for each accounting period. This method is similar toamordegrc, except thatamordegrchas a depreciation coefficient that is applied during the evaluation that is based on the asset life.- Parameters:
cost- adoublewhich specifes the cost of the assetissue- aGregorianCalendarissue date of the assetfirstPeriod- aGregorianCalendardate of the end of the first periodsalvage- adoublewhich specifies the asset's salvage value at the end of the life of the assetperiod- anintwhich specifies the periodrate- adoublewhich specifies the rate of depreciationbasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the depreciation - See Also:
- Example
-
convexity
public static double convexity(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
Returns the convexity for a security. Convexity is the sensitivity of the duration of a security to changes in yield. It is computed using the following:
where n is calculated from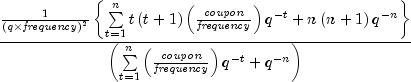
coupnum, and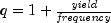 .
.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securitycoupon- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the convexity for a security - See Also:
- Example
-
coupdaybs
public static int coupdaybs(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the number of days starting with the beginning of the coupon period and ending with the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- an
intwhich specifies the number of days from the beginning of the coupon period to the settlement date - See Also:
- Example
-
coupdays
public static double coupdays(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the number of days in the coupon period containing the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the number of days in the coupon period that contains the settlement date - See Also:
- Example
-
coupdaysnc
public static int coupdaysnc(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the number of days starting with the settlement date and ending with the next coupon date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- an
intwhich specifies the number of days from the settlement date to the next coupon date - See Also:
- Example
-
coupncd
public static GregorianCalendar coupncd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the first coupon date which follows the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis- Returns:
- a
GregorianCalendarwhich specifies the next coupon date after the settlement date - See Also:
- Example
-
coupnum
public static int coupnum(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the number of coupons payable between the settlement date and the maturity date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- an
intwhich specifies the number of coupons payable between the settlement date and maturity date - See Also:
- Example
-
couppcd
public static GregorianCalendar couppcd(GregorianCalendar settlement, GregorianCalendar maturity, int frequency, DayCountBasis basis)
Returns the coupon date which immediately precedes the settlement date. For a good discussion on day count basis, see SIA Standard Securities Calculation Methods 1993, vol. 1, pages 17-35.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis- Returns:
- a
GregorianCalendarwhich specifies the previous coupon date before the settlement date - See Also:
- Example
-
disc
public static double disc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)
Returns the implied interest rate of a discount bond. The discount rate is the interest rate implied when a security is sold for less than its value at maturity in lieu of interest payments. It is computed using the following:
In the equation above,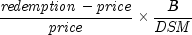
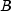 represents the number of
days in a year based on the annual basis and
represents the number of
days in a year based on the annual basis and
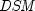 represents the number of days starting
with the settlement date and ending with the maturity date.
represents the number of days starting
with the settlement date and ending with the maturity date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityprice- adoublewhich specifies the security's price per $100 face valueredemption- adoublewhich specifies the security's redemption value per $100 face valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the discount rate for a security - See Also:
- Example
-
duration
public static double duration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
Returns the Macaulay duration of a security where the security has periodic interest payments. The Macaulay duration is the weighted-average time to the payments, where the weights are the present value of the payments. It is computed using the following:
In the equation above,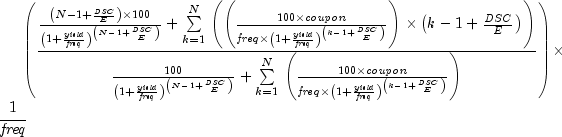
 represents the
number of days starting with the settlement date and ending with the next
coupon date.
represents the
number of days starting with the settlement date and ending with the next
coupon date. 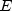 represents the number of days within
the coupon period.
represents the number of days within
the coupon period. 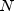 represents the number of
coupons payable from the settlement date to the maturity date.
represents the number of
coupons payable from the settlement date to the maturity date.
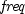 represents the frequency of the coupon
payments annually.
represents the frequency of the coupon
payments annually.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securitycoupon- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the annual duration of a security with periodic interest payments - See Also:
- Example
-
intrate
public static double intrate(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double redemption, DayCountBasis basis)
Returns the interest rate of a fully invested security. It is computed using the following:
In the equation above,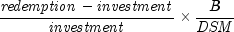
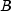 represents the number of
days in a year based on the annual basis, and
represents the number of
days in a year based on the annual basis, and
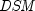 represents the number of days in the
period starting with the settlement date and ending with the maturity
date.
represents the number of days in the
period starting with the settlement date and ending with the maturity
date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityinvestment- adoublewhich specifies the amount investedredemption- adoublewhich specifies the amount to be received at maturitybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the interest rate for a fully invested security - See Also:
- Example
-
mduration
public static double mduration(GregorianCalendar settlement, GregorianCalendar maturity, double coupon, double yield, int frequency, DayCountBasis basis)
Returns the modified Macaulay duration for a security with an assumed par value of $100. It is computed using the following:
where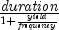
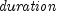 is calculated from
is calculated from
mduration.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securitycoupon- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldfrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the modified Macaulay duration for a security with an assumed par value of $100 - See Also:
- Example
-
price
public static double price(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
Returns the price, per $100 face value, of a security that pays periodic interest. It is computed using the following:
In the above equation,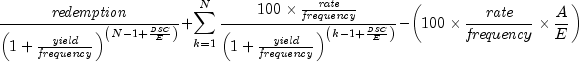
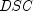 represents the
number of days in the period starting with the settlement date and ending
with the next coupon date.
represents the
number of days in the period starting with the settlement date and ending
with the next coupon date. 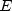 represents the number
of days within the coupon period.
represents the number
of days within the coupon period. 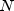 represents the number of coupons payable in the timeframe from the
settlement date to the redemption date.
represents the number of coupons payable in the timeframe from the
settlement date to the redemption date. 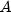 represents the number of days in the timeframe starting with the
beginning of coupon period and ending with the settlement date.
represents the number of days in the timeframe starting with the
beginning of coupon period and ending with the settlement date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityrate- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the price per $100 face value of a security that pays periodic interest - See Also:
- Example
-
price
public static double price(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
Returns the price of an odd last period coupon bond, given its yield.In the case of a short last period with one coupon period or less to redemption, the following formula is used:
![everymath{displaystyle}
P=left[frac{redemption+left(frac{100*rate}{frequency}*frac{DLC}{E}
right)}{1+left(frac{DSR}{E}*frac{yield}{frequency}right)}right]
-left[frac{A}{E}*frac{100*rate}{frequency}right]](eqn_0530.png)
where
Variable Description A Number of days from last coupon date before redemption to settlement date. DLC Number of days from last coupon date before redemption to redemption. DSR Number of days from settlement date to redemption date. E Number of days in the quasi-coupon period. In the case of a short last period with more than one coupon period to redemption, the following formula is used:
![everymath{displaystyle} begin{array}{lcl} P
& = & left[frac{redemption}{left(1+frac{yield}{frequency}
right)^{N-1+frac{DSC}{E}+frac{DLC}{NLL}}}right]
+left[sum^N_{K=1}frac{100*frac{rate}{frequency}}{left({1+
frac{yield}{frequency}}right)^{K-1+frac{DSC}{E}}}right]\[.7cm] & +
& left[frac{100*frac{rate}{frequency}*frac{DLC}{NLL}}{left({1+
frac{yield}{frequency}}right)^{N-1+frac{DSC}{E}+frac{DLC}{NLL}}}right]-
left[100*frac{rate}{frequency}*frac{A}{E}right] end{array}](eqn_0531.png)
where
Variable Description A Number of days from beginning of coupon period to settlement date. DLC Number of days from last coupon date before redemption to redemption. DSC Number of days from settlement date to next coupon date. E Number of days in coupon period in which the settlement date falls. N Number of coupons payable between settlement date and last coupon date before redemption. NLL Number of days in the full quasi-coupon period in which the odd last period falls. In the case of a long last period with one coupon period or less to redemption, the following formula is used:
![everymath{displaystyle}
P=left[frac{redemption+left(left(sumlimits^{NCL}_{i=1}
frac{{DLC}_i}{{NLL}_i}right)*frac{100*rate}{frequency}
right)}{1+left(sumlimits^{NCL}_{i=1}frac{{DSC}_i}{{NLL}_i}right)*
frac{yield}{frequency}}right]
-left[left(sumlimits^{NCL}_{i=1}frac{{A}_i}{{NLL}_i}right)*
frac{100*rate}{frequency}right]](eqn_0532.png)
where
Variable Description Ai Number of accrued days for the ith quasi-coupon period within the odd period counting forward from the last interest date before redemption. DLCi Number of days in the ith quasi-coupon period as delimited by the length of the actual coupon period. DSCi Number of days from settlement date (or beginning of quasi-coupon period) to next quasi-coupon within odd period (or to redemption date) for the ith quasi-coupon period. NCL Number of quasi-coupon periods that fit in odd period. NLLi Normal length in days of the full ith quasi-coupon period within odd last period. In the case of a long first period with more than one coupon period to redemption, the following formula is used:
![everymath{displaystyle} begin{array}{lcl} P
& = & left[frac{redemption}{left(1+frac{yield}{frequency}
right)^{N-1+frac{DSC}{E}+Nqf+frac{DLQ}{LQL}}}right]
+left[sum^N_{K=1}frac{100*frac{rate}{frequency}}{left({1+
frac{yield}{frequency}}right)^{K-1+frac{DSC}{E}}}right]\[.7cm] & +
& left[frac{100*frac{rate}{frequency}*left(sumlimits^{NCL}_{i=1}
frac{{DLC}_i}{{NLL}_i}right)}{left({1+frac{yield}{frequency}}
right)^{N-1+frac{DSC}{E}Nqf+frac{DLQ}{LQL}}}right]-
left[100*frac{rate}{frequency}*frac{A}{E}right] end{array}](eqn_0533.png)
where
Variable Description A Number of days from beginning of coupon period to settlement date. DLCi Number of days from last coupon date before redemption to first quasi-coupon or number of days in quasi-coupon. DLQ Number of days counted in the last quasi-coupon period within the last odd period. DSC Number of days from settlement date to next coupon date. E Number of days in coupon period in which the settlement falls. LQL Normal length in days of the last quasi-coupon period within the odd last period. N Number of coupons payable between settlement date and last coupon date before redemption. NCL Number of quasi-coupon periods that fit in odd period. NLLi Normal length in days of the full ith quasi-coupon period within odd last period. Nql Number of whole quasi-coupon periods between last coupon date before redemption and the redemption date. - Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securitylastCoupon- aGregorianCalendarlast interest date of the securityrate- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublethat indicates the bond price. - See Also:
- Example 1, Example 2, Example 3, Example 4
-
price
public static double price(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double yield, double redemption, int frequency, DayCountBasis basis)
Returns the price of an odd first period, coupon bond, given its yield.In the case of a short first period, the following formula is used:
![everymath{displaystyle}
begin{array}{lcl}
P & = & left[frac{redemption}{left(1+frac{yield}{frequency}right)^{
N-1+frac{DSC}{E}}}right]+left[frac{100*frac{rate}{frequency}*
frac{DFC}{E}}{left(1+frac{yield}{frequency}right)^frac{DSC}{E}}
right]\[.4cm]
& + & left[sum^N_{K=2}frac{100*frac{rate}{frequency}}{left({1+
frac{yield}{frequency}}right)^{K-1+frac{DSC}{E}}}right]-left[100*
frac{rate}{frequency}*frac{A}{E}right]
end{array}](eqn_0528.png)
where
Variable Description A Number of days from the beginning of coupon period to the settlement date (accrued days). DFC Number of days from the beginning of odd first coupon period ( issueDate) to the first coupon date.DSC Number of days from the settlement date to first coupon date. E Number of days in the quasi-coupon period in which the settlement date falls. N Number of coupons payable between settlement date and redemption date. In the case of a long first period, the following formula is used:
![everymath{displaystyle} begin{array}{lcl} P
& = & left[frac{redemption}{left(1+frac{yield}{frequency}
right)^{N-{Nqf}+frac{DSC}{E}}}right]+left[frac{100*
frac{rate}{frequency}*left[sumlimits^{NCF}_{i=1}
frac{{DFC}_i}{{NLF}_i}right]}{left(1+frac{yield}{frequency}
right)^{{Nqf}+frac{DSC}{E}}}right]\[.7cm] & + &
left[sum^N_{K=1}frac{100*frac{rate}{frequency}}{left({1+
frac{yield}{frequency}}right)^{K+{Nqf}+frac{DSC}{E}}}right]-
left[100*frac{rate}{frequency}*left[sumlimits^{NCF}_{i=1}
frac{A_i}{{NLF}_i}right]right] end{array}](eqn_0529.png)
where
Variable Description Ai Number of accrued days for the ith quasi-coupon period within the odd period. DFCi Number of days from the issueDateto the first quasi-coupon or number of days in the the quasi-coupon.DSC Number of days from the settlement date to the next coupon or quasi-coupon date. E Number of days in the quasi-coupon or coupon period in which the settlement date falls. N Number of coupon periods between the first real coupon date and redemption date. NCF Number of quasi-coupon periods that fall in the odd period. NLFi Number of days in the full ith quasi-coupon period within the odd period. Nqf Number of whole quasi-coupon periods between settlementandfirstCoupon.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityissueDate- aGregorianCalendarissue date of the securityfirstCoupon- aGregorianCalendarfirst coupon date of the securityrate- adoublewhich specifies the security's annual coupon rateyield- adoublewhich specifies the security's annual yieldredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublethat indicates the bond price. - See Also:
- Example 1, Example 2
-
pricedisc
public static double pricedisc(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double redemption, DayCountBasis basis)
Returns the price of a discount bond given the discount rate. It is computed using the following:
In the equation above,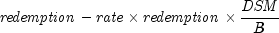
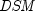 represents the
number of days starting at the settlement date and ending with the
maturity date.
represents the
number of days starting at the settlement date and ending with the
maturity date.  represents the number of days in a
year based on the annual basis.
represents the number of days in a
year based on the annual basis.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityrate- adoublewhich specifies the security's discount rateredemption- adoublewhich specifies the security's redemption value per $100 face valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the price per $100 face value of a discounted security - See Also:
- Example
-
pricemat
public static double pricemat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double yield, DayCountBasis basis)
Returns the price, per $100 face value, of a discount bond. It is computed using the following:
In the equation above,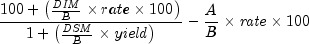
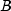 represents the number of
days in a year based on the annual basis.
represents the number of
days in a year based on the annual basis. 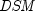 represents the number of days in the period starting with the settlement
date and ending with the maturity date.
represents the number of days in the period starting with the settlement
date and ending with the maturity date.  represents the number of days in the period starting with the issue date
and ending with the maturity date.
represents the number of days in the period starting with the issue date
and ending with the maturity date. 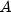 represents the
number of days in the period starting with the issue date and ending with
the settlement date.
represents the
number of days in the period starting with the issue date and ending with
the settlement date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityissue- aGregorianCalendarissue date of the securityrate- adoublewhich specifies the security's interest rate at issue dateyield- adoublewhich specifies the security's annual yieldbasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the price per $100 face value of a security that pays interest at maturity - See Also:
- Example
-
priceyield
public static double priceyield(GregorianCalendar settlement, GregorianCalendar maturity, double yield, double redemption, DayCountBasis basis)
Returns the price of a discount bond given the yield. It is computed using the following:
In the equation above,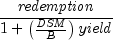
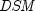 represents the
number of days starting at the settlement date and ending with the
maturity date.
represents the
number of days starting at the settlement date and ending with the
maturity date. 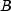 represents the number of days in a
year based on the annual basis.
represents the number of days in a
year based on the annual basis.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityyield- adoublewhich specifies the security's yieldredemption- adoublewhich specifies the security's redemption value per $100 face valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis- Returns:
- a
doublewhich specifies the price per $100 face value of a discounted security - See Also:
- Example
-
received
public static double received(GregorianCalendar settlement, GregorianCalendar maturity, double investment, double rate, DayCountBasis basis)
Returns the amount one receives when a fully invested security reaches the maturity date. It is computed using the following:
In the equation above,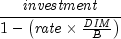
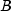 represents the number of
days in a year based on the annual basis, and
represents the number of
days in a year based on the annual basis, and
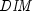 represents the number of days in the
period starting with the issue date and ending with the maturity date.
represents the number of days in the
period starting with the issue date and ending with the maturity date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityinvestment- adoublewhich specifies the amount invested in the securityrate- adoublewhich specifies the security's rate at issue datebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the amount received at maturity for a fully invested security - See Also:
- Example
-
tbilleq
public static double tbilleq(GregorianCalendar settlement, GregorianCalendar maturity, double rate)
Returns the bond-equivalent yield of a Treasury bill. It is computed using the following:If

otherwise,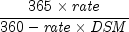
In the above equation,
 represents the
number of days starting at settlement date to maturity date.
represents the
number of days starting at settlement date to maturity date.- Parameters:
settlement- aGregorianCalendarsettlement date of the Treasury billmaturity- aGregorianCalendarmaturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.rate- adoublewhich specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).- Returns:
- a
doublewhich specifies the bond-equivalent yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity. - See Also:
- Example
-
tbillprice
public static double tbillprice(GregorianCalendar settlement, GregorianCalendar maturity, double rate)
Returns the price, per $100 face value, of a Treasury bill. It is computed using the following:
In the equation above,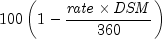
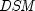 represents the
number of days in the period starting with the settlement date and ending
with the maturity date (any maturity date that is more than one calendar
year after the settlement date is excluded).
represents the
number of days in the period starting with the settlement date and ending
with the maturity date (any maturity date that is more than one calendar
year after the settlement date is excluded).- Parameters:
settlement- aGregorianCalendarsettlement date of the Treasury billmaturity- aGregorianCalendarmaturity date of the Treasury bill. The maturity cannot be more than a year after the settlementrate- adoublewhich specifies the Treasury bill's discount rate at issue date. The discount rate is an annualized rate of return based on the par value of the bills. The discount rate is calculated on a 360-day basis (twelve 30-day months).- Returns:
- a
doublewhich specifies the price per $100 face value for the Treasury bill - See Also:
- Example
-
tbillyield
public static double tbillyield(GregorianCalendar settlement, GregorianCalendar maturity, double price)
Returns the yield of a Treasury bill. It is computed using the following:
In the equation above,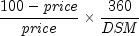
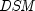 represents the
number of days in the period starting with the settlement date and ending
with the maturity date (any maturity date that is more than one calendar
year after the settlement date is excluded).
represents the
number of days in the period starting with the settlement date and ending
with the maturity date (any maturity date that is more than one calendar
year after the settlement date is excluded).- Parameters:
settlement- aGregorianCalendarsettlement date of the Treasury billmaturity- aGregorianCalendarmaturity date of the Treasury bill. The maturity cannot be more than a year after the settlement.price- adoublewhich specifies the Treasury bill's price per $100 face value- Returns:
- a
doublewhich specifies the yield for the Treasury bill. This is an annualized rate based on the purchase price of the bills and reflects the actual yield to maturity. - See Also:
- Example
-
yearfrac
public static double yearfrac(GregorianCalendar start, GregorianCalendar end, DayCountBasis basis)
Returns the fraction of a year represented by the number of whole days between two dates. It is computed using the following:
where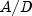
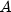 equals the number of days from
equals the number of days from
starttoend,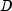 equals
annual basis.
equals
annual basis.- Parameters:
start- aGregorianCalendarstart date of the securityend- aGregorianCalendarend date of the securitybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the annual yield of a security that pays interest at maturity - See Also:
- Example
-
yield
public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, double rate, double price, double redemption, int frequency, DayCountBasis basis)
Returns the yield of a security that pays periodic interest. If there is one coupon period, use the following:
In the equation above,![{{{left( {{{it redemption} over {100}} +
{{it rate} over {it frequency}}} right) - left[ {{{it price} over
{100}} + left( {{A over E} times {{it rate} over {it frequency}}}
right)} right]} over {{{it price} over {100}} + left( {{A over E}
times {{it rate} over {it frequency}}} right)}}} times {{{{it
frequency} times E} over {it DSR}}}](eqn_0511.png)
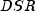 represents the number of
days in the period starting with the settlement date and ending with the
redemption date.
represents the number of
days in the period starting with the settlement date and ending with the
redemption date. 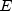 represents the number of days
within the coupon period.
represents the number of days
within the coupon period. 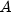 represents the number of
days in the period starting with the beginning of coupon period and
ending with the settlement date.
represents the number of
days in the period starting with the beginning of coupon period and
ending with the settlement date.
If there is more than one coupon period, use the following:
In the equation above,
 represents the
number of days in the period from the settlement to the next coupon date.
represents the
number of days in the period from the settlement to the next coupon date.
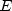 represents the number of days within the coupon
period.
represents the number of days within the coupon
period.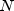 represents the number of coupons payable in
the period starting with the settlement date and ending with the
redemption date.
represents the number of coupons payable in
the period starting with the settlement date and ending with the
redemption date. 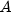 represents the number of days in
the period starting with the beginning of the coupon period and ending
with the settlement date.
represents the number of days in
the period starting with the beginning of the coupon period and ending
with the settlement date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityrate- adoublewhich specifies the security's annual coupon rateprice- adoublewhich specifies the security's price per $100 face valueredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the yield of a security that pays periodic interest - See Also:
- Example
-
yield
public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar lastCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)
Returns the yield of a security with an odd last coupon period that pays periodic interest.The yield is determined by finding the zero of the function desired price - computed price, where computed price is the output of
price(java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, double, double, double, int, com.imsl.finance.DayCountBasis).- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securitylastCoupon- aGregorianCalendarlast coupon date of the securityrate- adoublewhich specifies the security's annual coupon rateprice- adoublewhich specifies the security's price per $100 face valueredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the yield of a security that pays periodic interest - See Also:
- Example 1, Example 2, Example 3, Example 4
-
yield
public static double yield(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issueDate, GregorianCalendar firstCoupon, double rate, double price, double redemption, int frequency, DayCountBasis basis)
Returns the yield of a security with an odd first coupon period that pays periodic interest.The yield is determined by finding the zero of the function desired price - computed price, where computed price is the output of
price(java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, java.util.GregorianCalendar, double, double, double, int, com.imsl.finance.DayCountBasis).- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityissueDate- aGregorianCalendarissueDate date of the securityfirstCoupon- aGregorianCalendarfirst coupon date of the securityrate- adoublewhich specifies the security's annual coupon rateprice- adoublewhich specifies the security's price per $100 face valueredemption- adoublewhich specifies the security's redemption value per $100 face valuefrequency- anintwhich specifies the number of coupon payments per year:ANNUALfor annual,SEMIANNUALfor semiannual, andQUARTERLYfor quarterlybasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the yield of a security that pays periodic interest - See Also:
- Example 1, Example 2
-
yielddisc
public static double yielddisc(GregorianCalendar settlement, GregorianCalendar maturity, double price, double redemption, DayCountBasis basis)
Returns the annual yield of a discount bond. It is computed using the following:
In the equation above,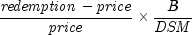
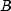 represents the number of
days in a year based on the annual basis, and
represents the number of
days in a year based on the annual basis, and
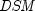 represents the number of days starting
with the settlement date and ending with the maturity date.
represents the number of days starting
with the settlement date and ending with the maturity date.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityprice- adoublewhich specifies the security's price per $100 face valueredemption- adoublewhich specifies the security's redemption value per $100 face valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the annual yield for a discounted security - See Also:
- Example
-
yieldmat
public static double yieldmat(GregorianCalendar settlement, GregorianCalendar maturity, GregorianCalendar issue, double rate, double price, DayCountBasis basis)
Returns the annual yield of a security that pays interest at maturity. It is computed using the following:
In the equation above,![{{{left[ {1 + left( {{{it DIM} over B}
times {it rate}} right)} right] - left[ {{{it price} over {100}} +
left( {{A over B} times {it rate}} right)} right]} over {{{it
price} over {100}} + left( {{A over B} times {it rate}} right)}}}
times {{B over {it DSM}}}](eqn_0520.png)
 represents the
number of days in the period starting with the issue date and ending with
the maturity date.
represents the
number of days in the period starting with the issue date and ending with
the maturity date. 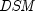 represents the number
of days in the period starting with the settlement date and ending with
the maturity date.
represents the number
of days in the period starting with the settlement date and ending with
the maturity date. 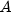 represents the number of days
in the period starting with the issue date and ending with the settlement
date.
represents the number of days
in the period starting with the issue date and ending with the settlement
date. 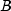 represents the number of days in a year
based on the annual basis.
represents the number of days in a year
based on the annual basis.- Parameters:
settlement- aGregorianCalendarsettlement date of the securitymaturity- aGregorianCalendarmaturity date of the securityissue- aGregorianCalendarissue date of the securityrate- adoublewhich specifies the security's interest rate at date of issueprice- adoublewhich specifies the security's price per $100 face valuebasis- aDayCountBasisobject which contains the type of day count basis to use. SeeDayCountBasis.- Returns:
- a
doublewhich specifies the annual yield of a security that pays interest at maturity - See Also:
- Example
-
-