- java.lang.Object
-
- com.imsl.stat.ARSeasonalFit
-
- All Implemented Interfaces:
- Serializable
public class ARSeasonalFit extends Object implements Serializable
Estimates the optimum seasonality parameters for a time series using an autoregressive model, AR(p), to represent the time series.ARMA time series modeling assumes the time series is stationary. Seasonal trends and cycles violate this assumption, which can lead to inaccurate predictions. However, in many cases the nonstationary series can be transformed into a stationary series by first differencing the series. For example, if the correlation is strong from one period to the next, the series might be differenced by a lag of 1. Instead of fitting a model to the original series
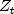 , the model is fitted to the
transformed series:
, the model is fitted to the
transformed series: 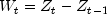 . Higher order
lags or differences are warranted if the series has cycles every 4 or 13
weeks. Class
. Higher order
lags or differences are warranted if the series has cycles every 4 or 13
weeks. Class ARSeasonalFitis designed to help identify the optimum differencing for a series with seasonal trends or cycles.ARSeasonalFitassumes the original series has no missing values, is equally spaced in time and is not centered before computing the optimum differencing. However, by default the transformed series is centered using the mean of that series. Users can change this default using thesetCentersetCenteris set toNO_CENTERCENTER_MEANCENTER_MEDIANsetCenteris set toCENTER_MEANorCENTER_MEDIANthen the differenced series,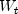 is centered before determination
of minimum AIC and optimum lag.
is centered before determination
of minimum AIC and optimum lag. For every combination of rows in
sInitialanddInitial, the series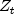 is converted to the seasonally
adjusted series using the following computation
is converted to the seasonally
adjusted series using the following computation
where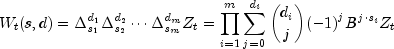
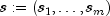 ,
, 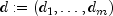 represent specific rows of arrays
represent specific rows of arrays sInitialanddInitialrespectively, and m is the number of differences, or m=sInitial[0].length.This transformation of the series
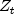 to
to  is computed using the
is computed using the Differenceclass. After this transformation the transformed series
is centered, unless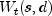
NO_CENTERis specified, and theARAutoUnivariate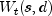 .
.
This procedure is repeated for every possible combination of rows in
sInitialanddInitial. The series with the minimum AIC is identified as the optimum representation and returned in the methodsgetAROrdergetOptimumSgetOptimumDgetAICgetARgetTransformedTimeSeries- See Also:
- Example, Serialized Form
-
-
Field Summary
Fields Modifier and Type Field and Description static intCENTER_MEANIndicates the transformed series should be centered using the average of the differenced series.static intCENTER_MEDIANIndicates the transformed series should be centered using the median of the differenced series.static intNO_CENTERIndicates the transformed series should not be centered.
-
Constructor Summary
Constructors Constructor and Description ARSeasonalFit(int maxlag, int[][] sInitial, double[] z)Constructor forARSeasonalFit.
-
Method Summary
Methods Modifier and Type Method and Description voidcompute()Computes the minimum AIC and optimum values for s and d based upon the candidates provided insInitialanddInitial, and computes the values for the transformed series,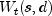 .
.doublegetAIC()Returns the final estimate for Akaike's Information Criterion (AIC) at the optimum.double[]getAR()Returns the final autoregressive parameter estimates at the optimum in the transformed series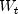 .
.intgetAROrder()Returns optimum number of lags, p, for the optimum autoregressive AR(p) model.intgetCenter()Returns the current setting for centering the input time series.int[][]getDInitial()Returns the candidate values for d to evaluate.booleangetExclude()Returns the current setting for excluding or replacing the inital values in the transformed series.intgetMaxlag()Returns the maximum lag used to fit the AR(p) model.intgetNLost()Returns the number of values in the initial part of the series lost to differencing.int[]getOptimumD()Returns the optimum values for d selected among the candidates indInitial.int[]getOptimumS()Returns the optimum values for s selected among the candidates insInitial.int[][]getSInitial()Returns the the candidate values for s to evaluate.double[]getTimeSeries()Returns the time series.double[]getTransformedTimeSeries()Returns the transformed series, .
.voidsetCenter(int center)Controls centering of the differenced series.voidsetDInitial(int[][] dInitial)Sets the candidate values for selecting the optimum seasonal adjustment prior to calling the compute method.voidsetExclude(boolean exclude)Controls whether to exclude or replace the inital values in the transformed series.
-
-
-
Field Detail
-
CENTER_MEAN
public static final int CENTER_MEAN
Indicates the transformed series should be centered using the average of the differenced series.- See Also:
- Constant Field Values
-
CENTER_MEDIAN
public static final int CENTER_MEDIAN
Indicates the transformed series should be centered using the median of the differenced series.- See Also:
- Constant Field Values
-
NO_CENTER
public static final int NO_CENTER
Indicates the transformed series should not be centered.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
ARSeasonalFit
public ARSeasonalFit(int maxlag, int[][] sInitial, double[] z)Constructor forARSeasonalFit.- Parameters:
maxlag- anintscalar specifying the maximum lag allowed when fitting an AR(p) model.sInitial- anintmatrix where each row represents seasonal differences to evaluate. The number of columns insInitialrepresent the number of differences to perform. All values ofsInitialmust be greater than zero.z- an inputdoublearray containing the time series.
-
-
Method Detail
-
compute
public void compute() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionComputes the minimum AIC and optimum values for s and d based upon the candidates provided insInitialanddInitial, and computes the values for the transformed series,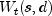 .
.
Warnings are printed if a row in
sInitialis skipped due to too many observations lost in the differenced series or if problems occurred computing the optimum AIC using the differenced series.- Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
getAIC
public double getAIC()
Returns the final estimate for Akaike's Information Criterion (AIC) at the optimum.- Returns:
- a
doubleequal to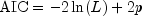 , where L is the value of the maximum
likelihood function evalutated at the parameter estimates.
, where L is the value of the maximum
likelihood function evalutated at the parameter estimates.
-
getAR
public double[] getAR() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionReturns the final autoregressive parameter estimates at the optimum in the transformed series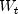 .
.- Returns:
- a
doublearray containing the estimates for the autoregressive parameters - Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
getAROrder
public int getAROrder()
Returns optimum number of lags, p, for the optimum autoregressive AR(p) model. This is the value of p for the transformed series,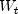 .
.- Returns:
- an
intcontaining the optimum number of lags in the autoregressive model used to fit the transformed series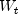 .
.
-
getCenter
public int getCenter()
Returns the current setting for centering the input time series.- Returns:
- an
intcontaining the setting for center equal to 0, 1, or 2, which impliesNO_CENTERCENTER_MEANCENTER_MEDIAN
-
getDInitial
public int[][] getDInitial()
Returns the candidate values for d to evaluate.- Returns:
- an
intmatrix containing the candidate values for d to evaluate
-
getExclude
public boolean getExclude()
Returns the current setting for excluding or replacing the inital values in the transformed series.If exclude is
true, then inital values in the transformed series that cannot be computed are set to missing,NaN. This ensures that the length of the transformed series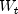 is equal to the length of the time series,
is equal to the length of the time series, z.length. If exclude is set tofalse, then inital values in the transformed series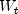 that cannot be computed
are removed. This makes the length of the transformed series
that cannot be computed
are removed. This makes the length of the transformed series 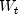 equal to
equal to z.length-nLost where nLost is the number of lost values obtained from methodgetNLost
-
getMaxlag
public int getMaxlag()
Returns the maximum lag used to fit the AR(p) model.- Returns:
- an
intscalar containing the maximum lag allowed when fitting an AR(p) model
-
getNLost
public int getNLost() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionReturns the number of values in the initial part of the series lost to differencing.- Returns:
- an
intcontaining the number of values in the initial part of the series lost to differencing. These lost values will be set to missing or dropped in the transformed series, depending upon the setting for exclude. - Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
getOptimumD
public int[] getOptimumD() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionReturns the optimum values for d selected among the candidates indInitial.- Returns:
- an
intarray of lengthdInitial[0].lengthcontaining the optimum values for d selected among the candidates indInitial - Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
getOptimumS
public int[] getOptimumS() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionReturns the optimum values for s selected among the candidates insInitial.- Returns:
- an
intarray of lengthsInitial[0].lengthcontaining the optimum values for s selected among the candidates insInitial - Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
getSInitial
public int[][] getSInitial()
Returns the the candidate values for s to evaluate.- Returns:
- an
intmatrix containing the candidate values for s to evaluate
-
getTimeSeries
public double[] getTimeSeries()
Returns the time series.- Returns:
- a
doublearray containing the time series values
-
getTransformedTimeSeries
public double[] getTransformedTimeSeries() throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAExceptionReturns the transformed series, .
.
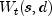 is an array of length
is an array of length z.lengthorz.length-nLostcontaining the optimum seasonally adjusted, autoregressive series, wherenLostis the first lost observations in this series that are dropped due to differencing. If the missing values are not dropped the firstnLostvalues of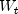 will be set (
will be set (Double.NaN). ThegetNLostnLost.The seasonal adjustment is done by selecting optimum values for
 ,
,  (m is number of differences or
(m is number of differences or sIinitial[0].length) and p in the AR model:
where
 is the original time series, B
is the backward shift operator defined by
is the original time series, B
is the backward shift operator defined by  ,
,  is
Gaussian white noise with
is
Gaussian white noise with ![E[a_t]=0](eqn_3925.png) and
and ![mbox{Var}[a_t]=sigma^2](eqn_3926.png) ,
,  ,
,
 , with
, with 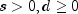 , and
, and 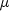 is a centering parameter for
the differenced series.
is a centering parameter for
the differenced series.- Returns:
- a
doublearray of lengthz.lengthorz.length-nLost, depending upon the setting forsetExclude - Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singularARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too smallARMA.NewInitialGuessException- is thrown if the iteration has not made good progressARMA.IllConditionedException- is thrown if the problem is ill-conditionedARMA.TooManyITNException- is thrown if the maximum number of iterations is exceededARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceededARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceededARMAMaxLikelihood.NonStationaryException- is thrown if the final maximum likelihood estimates for the time series are nonstationaryARMAMaxLikelihood.NonInvertibleException- is thrown if the final maximum likelihood estimates for the time series are noninvertibleARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms usingsetMAare noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input triangular matrix is singular.
-
setCenter
public void setCenter(int center)
Controls centering of the differenced series.- Parameters:
center- anintscalar value equalNO_CENTERCENTER_MEANCENTER_MEDIANcenter=CENTER_MEAN
-
setDInitial
public void setDInitial(int[][] dInitial)
Sets the candidate values for selecting the optimum seasonal adjustment prior to calling the compute method.- Parameters:
dInitial- anintarray of candidate values for d to evaluate. All values must be non-negative.dInitialmust have the same number of differences (columns) assInitial. By default,dInitialis initialized to all ones.
-
setExclude
public void setExclude(boolean exclude)
Controls whether to exclude or replace the inital values in the transformed series.If exclude is
true, then inital values in the transformed series that cannot be computed are set to missing,NaN. This ensures that the length of the transformed series is equal to the length of the time series,
is equal to the length of the time series, z.length. If exclude is set tofalse, then inital values in the transformed series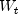 that cannot be computed
are removed. This makes the length of the transformed series
that cannot be computed
are removed. This makes the length of the transformed series  equal to
equal to z.length-nLost where nLost is the number of lost values obtained from methodgetNLost- Parameters:
exclude- abooleanvalue that controls whether values in that cannot be calculated are
dropped or set to missing. Missing values are set to
that cannot be calculated are
dropped or set to missing. Missing values are set to
Double.NaN. By default,exclude=true
-
-