- java.lang.Object
-
- com.imsl.stat.AutoARIMA
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class AutoARIMA extends Object implements Serializable, Cloneable
Automatically identifies time series outliers, determines parameters of a multiplicative seasonal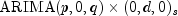 model and produces forecasts that incorporate the effects of
outliers whose effects persist beyond the end of the series.
model and produces forecasts that incorporate the effects of
outliers whose effects persist beyond the end of the series.
Class
AutoARIMAdetermines the parameters of a multiplicative seasonal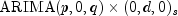 model, and
then uses the fitted model to identify outliers and prepare forecasts. The
order of this model can be specified or automatically determined through use
of an overloaded
model, and
then uses the fitted model to identify outliers and prepare forecasts. The
order of this model can be specified or automatically determined through use
of an overloaded computemethod. Potential missing values in the time series are estimated prior to the parameter and outlier computations.The
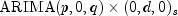 model
handled by class
model
handled by class AutoARIMAhas the following form:
where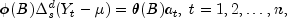
and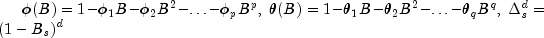
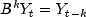
It is assumed that all roots of
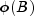 and
and
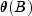 lie outside the unit circle. Clearly, if
lie outside the unit circle. Clearly, if
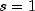 the model reduces to the traditional
the model reduces to the traditional 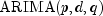 model.
model.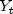 is the unobserved, outlier-free time series with
mean
is the unobserved, outlier-free time series with
mean 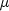 , and white noise
, and white noise 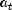 . This
model is referred to as the underlying, outlier-free model. Class
. This
model is referred to as the underlying, outlier-free model. Class AutoARIMAdoes not assume that this series is observable. It assumes that the observed values might be contaminated by one or more outliers, whose effects are added to the underlying outlier-free series: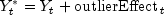
Outlier identification uses the algorithm developed by Chen and Liu (1993). Outliers are classified into 1 of 5 types:
- innovational
- additive
- level shift
- temporary change and
- unable to identify
Once the model parameters are estimated and the outliers are identified, class
AutoARIMAestimates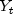 , the
outlier-free series representation of the data, by removing the estimated
outlier effects. Parameter estimation and outlier detection are based on
methods from class
, the
outlier-free series representation of the data, by removing the estimated
outlier effects. Parameter estimation and outlier detection are based on
methods from class ARMAOutlierIdentification.Using the information about the adjusted
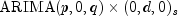 model and the removed outliers, forecasts are
then prepared for the outlier-free series. Outlier effects are added to these
forecasts to produce a forecast for the observed series,
model and the removed outliers, forecasts are
then prepared for the outlier-free series. Outlier effects are added to these
forecasts to produce a forecast for the observed series, 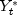 . If there are no outliers, then the forecasts for the
outlier-free series and the observed series will be identical.
. If there are no outliers, then the forecasts for the
outlier-free series and the observed series will be identical.Model selection techniques
Users have an option of either specifying specific values for
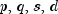 or have class
or have class AutoARIMAautomatically select best fit values. Model selection can be conducted in one of three ways listed below depending upon whichcomputemethod of classAutoARIMAis invoked.Technique 1: Automatic
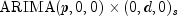 Selection
SelectionThis technique, chosen by use of method
compute(int maxlag), tries to fit a model of the form
to the outlier free series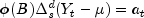
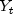 .
.
It initially searches for the
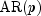 representation with minimum value of the chosen information criterion (AIC,
AICC or BIC) for the noisy data, where
representation with minimum value of the chosen information criterion (AIC,
AICC or BIC) for the noisy data, where 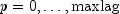 .
.If the user calls methods
setPeriodsandsetDifferenceOrdersprior to invoking thecomputemethod, then the values in arraysperiodsandordersare included in the search to find an optimum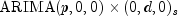 representation of the series. Here, every possible
combination of values for s, d in
representation of the series. Here, every possible
combination of values for s, d in periodsandorders, respectively, are examined. The best found model order is then used as input for the parameter and outlier detection routine.The optimum values for p, q, s and d are returned through method
getOptimumModelOrder.Technique 2: Grid Search
This technique, chosen by means of method
compute(int[] arOrders, int[] maOrders), conducts a grid search for p and q using all possible combinations of candidate values inarOrdersandmaOrders.If methods
setPeriodsandsetDifferenceOrdersare called prior to invoking thecomputemethod, then the grid search is extended to include the candidate values for s and d given in arraysperiodsandorders, respectively.If method
setDifferenceOrdersis not called prior tocompute, then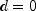 by default,
and therefore no seasonal adjustment is attempted. The grid search is then
restricted to searching for optimum values of p and q only.
by default,
and therefore no seasonal adjustment is attempted. The grid search is then
restricted to searching for optimum values of p and q only.The optimum values for p, q, s and d are contained in the array returned by method
getOptimumModelOrder.Technique 3: Specified
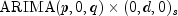 Model
ModelIn the third technique, selectable by means of method
compute(int p, int q, int s, int d), specific values for p, q, s and d are given. This technique has essentially the same functionality as classARMAOutlierIdentificationbut with the additional option of missing value estimation.Outliers
The algorithm of Chen and Liu (1993) is used to identify outliers. The number of outliers identified is returned via method
getNumberOfOutliers. Both the time and classification for these outliers are contained in the matrix returned by methodgetOutlierStatistics. Outliers are classified into one of five categories based upon the standardized statistic for each outlier type. The time at which the outlier occurred is given in the first column of the returned matrix. The outlier identifier returned in the second column is according to the descriptions in the following table:Outlier Identifier Name General Description INNOVATIONALInnovational Outlier (IO) Innovational outliers persist. That is, there is an initial impact at the time the outlier occurs. This effect continues in a lagged fashion with all future observations. The lag coefficients are determined by the coefficients of the underlying 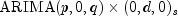 model.
model.ADDITIVEAdditive Outlier (AO) Additive outliers do not persist. As the name implies, an additive outlier affects only the observation at the time the outlier occurs. Hence additive outliers have no effect on future forecasts. LEVEL_SHIFTLevel Shift (LS) Level shift outliers persist. They have the effect of either raising or lowering the mean of the series starting at the time the outlier occurs. This shift in the mean is abrupt and permanent. TEMPORARY_CHANGETemporary Change (TC) Temporary change outliers persist and are similar to level shift outliers with one major exception. Like level shift outliers, there is an abrupt change in the mean of the series at the time this outlier occurs. However, unlike level shift outliers, this shift is not permanent. The TC outlier gradually decays, eventually bringing the mean of the series back to its original value. The rate of this decay is modeled using method setDelta. The default ofdelta = 0.7is the value recommended for general use by Chen and Liu (1993).UNABLE_TO_IDENTIFYUnable to Identify (UI) If an outlier is identified as the last observation, then the algorithm is unable to determine the outlier's classification. For forecasting, a UI outlier is treated as an IO outlier. That is, its effect is lagged into the forecasts. Except for additive outliers (AO), the effect of an outlier persists to observations following that outlier. Forecasts produced by methods of class
AutoARIMAtake this into account.For more information on forecasting an outlier contaminated series, see the description of class
ARMAOutlierIdentification.- See Also:
- Example 1, Example 2, Example 3, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static classAutoARIMA.NoAcceptableModelFoundExceptionNo appropriate ARIMA model could be found.
-
Field Summary
Fields Modifier and Type Field and Description static intADDITIVEIndicates detection of an additive outlier.static intAICIndicates that Akaike's information criterion (AIC) is used in the optimum model determination.static intAICCIndicates that Akaike's corrected information criterion (AICC) is used in the optimum model determination.static intBICIndicates that the Bayesian information criterion (BIC) is used in the optimum model determination.static intINNOVATIONALIndicates detection of an innovational outlier.static intLEVEL_SHIFTIndicates detection of a level shift outlier.static intTEMPORARY_CHANGEIndicates detection of a temporary change outlier.static intUNABLE_TO_IDENTIFYIndicates detection of an outlier that cannnot be categorized.
-
Constructor Summary
Constructors Constructor and Description AutoARIMA(int[] times, double[] x)Constructor forAutoARIMA.
-
Method Summary
Methods Modifier and Type Method and Description voidcompute(int maxlag)Estimates potential missing values, detects and determines outliers and simultaneously fits an optimum model from a set of different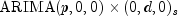 models to the outlier free
time series.
models to the outlier free
time series.voidcompute(int[] arOrders, int[] maOrders)Estimates potential missing values, detects and determines outliers and simultaneously fits an optimum model from a set of different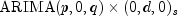 models to the outlier free
time series.
models to the outlier free
time series.voidcompute(int p, int q, int s, int d)Estimates potential missing values, detects and determines outliers and simultaneously fits an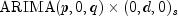 model to the outlier free time series.
model to the outlier free time series.voidforecast(int nForecast)Computes forecasts, associated probability limits and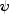 weights for the given outlier contaminated time series.
weights for the given outlier contaminated time series.doublegetAIC()Returns Akaike's information criterion (AIC) for the optimum model.doublegetAICC()Returns Akaike's Corrected Information Criterion (AICC) for the optimum model.double[]getAR()Returns the final autoregressive parameter estimates of the optimum model.doublegetBIC()Returns the Bayesian Information Criterion (BIC) for the optimum model.int[]getCompleteTimes()Returns all time points at which the original series was observed, including values for times with missing values inx.double[]getCompleteTimeSeries()Returns the original series with potentially missing values replaced by estimates.doublegetConstant()Returns the constant parameter estimate for the optimum model.double[]getDeviations()Returns the deviations used for calculating the forecast confidence limits.double[]getForecast()Returns forecasts for the original outlier contaminated series.double[]getMA()Returns the final moving average parameter estimates of the optimum model.intgetNumberOfOutliers()Returns the number of outliers detected.int[]getOptimumModelOrder()Returns the order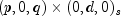 of the
optimum model.
of the
optimum model.double[]getOutlierFreeForecast()Returns forecasts for the outlier free series.double[]getOutlierFreeSeries()Returns the outlier free series.int[][]getOutlierStatistics()Returns the outlier statistics.double[]getPsiWeights()Returns the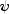 weights of the infinite order
moving average form of the model.
weights of the infinite order
moving average form of the model.double[]getResiduals()Returns the residuals.doublegetResidualStandardError()Returns the residual standard error of the outlier free series.voidsetAccuracyTolerance(double epsilon)Sets the tolerance value controlling the accuracy of the parameter estimates.voidsetConfidence(double confidence)Sets the confidence level for calculating confidence limit deviations returned bygetDeviations.voidsetCriticalValue(double critical)Sets the critical value used as a threshold during outlier detection.voidsetDelta(double delta)Sets the dampening effect parameter.voidsetDifferenceOrders(int[] orders)Defines the orders of the periodic differences used in the determination of the optimum model.voidsetMaximumARLag(int maxARLag)Defines the maximum AR lag used in the determination of the optimum (s,d) combination of methodcompute(int[] arOrders, int[] maOrders).voidsetModelSelectionCriterion(int infoCriterion)Sets the model selection criterion.voidsetPeriods(int[] periods)Defines the periods used in the determination of the optimum model.voidsetRelativeError(double relativeError)Sets the stopping criterion for use in the nonlinear equation solver.
-
-
-
Field Detail
-
ADDITIVE
public static final int ADDITIVE
Indicates detection of an additive outlier.- See Also:
- Constant Field Values
-
AIC
public static final int AIC
Indicates that Akaike's information criterion (AIC) is used in the optimum model determination.- See Also:
- Constant Field Values
-
AICC
public static final int AICC
Indicates that Akaike's corrected information criterion (AICC) is used in the optimum model determination.- See Also:
- Constant Field Values
-
BIC
public static final int BIC
Indicates that the Bayesian information criterion (BIC) is used in the optimum model determination.- See Also:
- Constant Field Values
-
INNOVATIONAL
public static final int INNOVATIONAL
Indicates detection of an innovational outlier.- See Also:
- Constant Field Values
-
LEVEL_SHIFT
public static final int LEVEL_SHIFT
Indicates detection of a level shift outlier.- See Also:
- Constant Field Values
-
TEMPORARY_CHANGE
public static final int TEMPORARY_CHANGE
Indicates detection of a temporary change outlier.- See Also:
- Constant Field Values
-
UNABLE_TO_IDENTIFY
public static final int UNABLE_TO_IDENTIFY
Indicates detection of an outlier that cannnot be categorized.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
AutoARIMA
public AutoARIMA(int[] times, double[] x)Constructor forAutoARIMA.- Parameters:
times- anintarray of lengthnObs, wherenObsis the number of observed time series values, containing the time points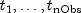 at which
the time series was observed. It is required that
at which
the time series was observed. It is required that
 are in
strictly increasing order. Times for missing values are
identified as non-incremental gaps in this series. A gap
of missing values in
are in
strictly increasing order. Times for missing values are
identified as non-incremental gaps in this series. A gap
of missing values in xis assumed if the difference between two consecutive values is greater than 1, i.e.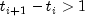 . The difference
is the number of missing values in the gap.
. The difference
is the number of missing values in the gap.x- adoublearray containing the observations at the times given in array
at the times given in array times. This series can contain outliers and missing observations.
-
-
Method Detail
-
compute
public final void compute(int maxlag) throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAException, ZeroPolynomial.DidNotConvergeException, SingularMatrixException, Cholesky.NotSPDException, AutoARIMA.NoAcceptableModelFoundExceptionEstimates potential missing values, detects and determines outliers and simultaneously fits an optimum model from a set of different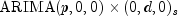 models to the outlier free
time series.
models to the outlier free
time series.- Parameters:
maxlag- the maximum value for p allowed when fitting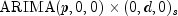 models to the given series,
models to the given series, 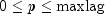 . It is required that
. It is required that 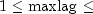
x.length. The optimum model is determined according to the model selection
criterion chosen by the user, see method
model is determined according to the model selection
criterion chosen by the user, see method setModelSelectionCriterion.- Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singular.ARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too small.ARMA.NewInitialGuessException- is thrown if the iteration has not made good progress.ARMA.IllConditionedException- is thrown if the problem is ill-conditioned.ARMA.TooManyITNException- is thrown if the maximum number of iterations is exceeded.ARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceeded.ARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceeded.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input matrix to ARAutoUnivariate is singular.ARMAMaxLikelihood.NonInvertibleException- is thrown if the intermediate or final maximum likelihood estimates for the time series are noninvertible.ARMAMaxLikelihood.NonStationaryException- is thrown if the intermediate or final maximum likelihood estimates for the time series are nonstationary.ARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms are noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ZeroPolynomial.DidNotConvergeException- is thrown if the algorithm computing the roots of the AR- or MA- polynomial does not converge.SingularMatrixException- is thrown if during the computation of a small perturbation of the matrix product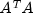 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is singular.
weights, is singular.Cholesky.NotSPDException- is thrown if during the computation of a small perturbation of the matrix product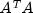 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is not positive definite.
weights, is not positive definite.AutoARIMA.NoAcceptableModelFoundException- is thrown if no appropriate ARIMA model for the given time series could be found.
-
compute
public final void compute(int[] arOrders, int[] maOrders) throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAException, ZeroPolynomial.DidNotConvergeException, SingularMatrixException, Cholesky.NotSPDException, AutoARIMA.NoAcceptableModelFoundExceptionEstimates potential missing values, detects and determines outliers and simultaneously fits an optimum model from a set of different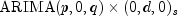 models to the outlier free
time series.
models to the outlier free
time series.- Parameters:
arOrders- anintarray containing all possible AR orders to consider in the optimum model search. It is required that all values inarOrdersare greater than or equal to zero.maOrders- anintarray containing all possible MA orders to consider in the optimum model search. It is required that all values inmaOrdersare greater than or equal to zero.- Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singular.ARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too small.ARMA.NewInitialGuessException- is thrown if the iteration has not made good progress.ARMA.IllConditionedException- is thrown if the problem is ill-conditioned.ARMA.TooManyITNException- is thrown if the maximum number of iterations is exceeded.ARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceeded.ARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceeded.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input matrix to ARAutoUnivariate is singular.ARMAMaxLikelihood.NonInvertibleException- is thrown if the intermediate or final maximum likelihood estimates for the time series are noninvertible.ARMAMaxLikelihood.NonStationaryException- is thrown if the intermediate or final maximum likelihood estimates for the time series are nonstationary.ARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms are noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ZeroPolynomial.DidNotConvergeException- is thrown if the algorithm computing the roots of the AR- or MA- polynomial does not converge.SingularMatrixException- is thrown if during the computation of a small perturbation of the matrix product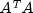 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is singular.
weights, is singular.Cholesky.NotSPDException- is thrown if during the computation of a small perturbation of the matrix product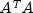 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is not positive definite.
weights, is not positive definite.AutoARIMA.NoAcceptableModelFoundException- is thrown if no appropriate ARIMA model for the given time series could be found.
-
compute
public final void compute(int p, int q, int s, int d) throws ARMA.MatrixSingularException, ARMA.TooManyCallsException, ARMA.IncreaseErrRelException, ARMA.NewInitialGuessException, ARMA.IllConditionedException, ARMA.TooManyITNException, ARMA.TooManyFcnEvalException, ARMA.TooManyJacobianEvalException, ARAutoUnivariate.TriangularMatrixSingularException, ARMAMaxLikelihood.NonInvertibleException, ARMAMaxLikelihood.NonStationaryException, ARMAMaxLikelihood.InitialMAException, ZeroPolynomial.DidNotConvergeException, SingularMatrixException, Cholesky.NotSPDException, AutoARIMA.NoAcceptableModelFoundExceptionEstimates potential missing values, detects and determines outliers and simultaneously fits an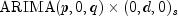 model to the outlier free time series.
model to the outlier free time series.- Parameters:
p- a non-negative scalarint, the order of the AR part of the model.q- a non-negative scalarint, the order of the MA part of the model.s- a positive scalarint, the period of the difference used in the model.d- a non-negative scalarint, the order of the difference used in the model.- Throws:
ARMA.MatrixSingularException- is thrown if the input matrix is singular.ARMA.TooManyCallsException- is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.ARMA.IncreaseErrRelException- is thrown if the bound for the relative error is too small.ARMA.NewInitialGuessException- is thrown if the iteration has not made good progress.ARMA.IllConditionedException- is thrown if the problem is ill-conditioned.ARMA.TooManyITNException- is thrown if the maximum number of iterations is exceeded.ARMA.TooManyFcnEvalException- is thrown if the maximum number of function evaluations is exceeded.ARMA.TooManyJacobianEvalException- is thrown if the maximum number of Jacobian evaluations is exceeded.ARAutoUnivariate.TriangularMatrixSingularException- is thrown if the input matrix to ARAutoUnivariate is singular.ARMAMaxLikelihood.NonInvertibleException- is thrown if the intermediate or final maximum likelihood estimates for the time series are noninvertible.ARMAMaxLikelihood.NonStationaryException- is thrown if the intermediate or final maximum likelihood estimates for the time series are nonstationary.ARMAMaxLikelihood.InitialMAException- is thrown if the initial values provided for the moving average terms are noninvertible. In this case,ARMAMaxLikelihoodterminates and does not compute the time series estimates.ZeroPolynomial.DidNotConvergeException- is thrown if the algorithm computing the roots of the AR- or MA- polynomial does not converge.SingularMatrixException- is thrown if during the computation of a small perturbation of the matrix product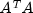 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is singular.
weights, is singular.Cholesky.NotSPDException- is thrown if during the computation of a small perturbation of the matrix product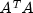 ,
it is found that A, the matrix used in the determination of the
,
it is found that A, the matrix used in the determination of the
 weights, is not positive definite.
weights, is not positive definite.AutoARIMA.NoAcceptableModelFoundException- is thrown if no appropriate ARIMA model for the given time series could be found.
-
forecast
public final void forecast(int nForecast)
Computes forecasts, associated probability limits and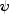 weights for the given outlier contaminated time series. Note that one of the
weights for the given outlier contaminated time series. Note that one of the
computemethods must be invoked first before invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.- Parameters:
nForecast- anintscalar representing the number of forecasts that will be computed.nForecastmust be greater than 0. Forecast origin is the time point of the last observed value in the time series,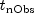 . Forecasts are
computed for lead times
. Forecasts are
computed for lead times
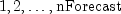 ,
i.e. time points
,
i.e. time points
 .
.
-
getAIC
public double getAIC()
Returns Akaike's information criterion (AIC) for the optimum model.- Returns:
- a
doublescalar containing Akaike's information criterion (AIC) for the optimum outlier free series. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getAICC
public double getAICC()
Returns Akaike's Corrected Information Criterion (AICC) for the optimum model.- Returns:
- a
doublescalar containing Akaike's Corrected Information Criterion (AICC) for the optimum outlier free series. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getAR
public double[] getAR()
Returns the final autoregressive parameter estimates of the optimum model. Note that one of thecomputemethods must be invoked first before invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.- Returns:
- a
doublearray containing the final autoregressive parameter estimates. If the optimum model has no AR component then a zero-length array is returned.
-
getBIC
public double getBIC()
Returns the Bayesian Information Criterion (BIC) for the optimum model.- Returns:
- a
doublescalar containing the Bayesian Information Criterion (BIC) for the optimum outlier free series. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getCompleteTimes
public int[] getCompleteTimes()
Returns all time points at which the original series was observed, including values for times with missing values inx.- Returns:
- an
intarray of lengthtimes[times.length-1]-times[0]+1containing the times at which the time series (including missing values) was observed. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getCompleteTimeSeries
public double[] getCompleteTimeSeries()
Returns the original series with potentially missing values replaced by estimates.- Returns:
- a
doublearray containing the original time series with missing values replaced by estimates. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getConstant
public double getConstant()
Returns the constant parameter estimate for the optimum model. Note that one of thecomputemethods must be invoked first before invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.- Returns:
- a
doublescalar containing the constant parameter estimate for the optimum model.
-
getDeviations
public double[] getDeviations()
Returns the deviations used for calculating the forecast confidence limits.- Returns:
- a
doublearray of lengthnForecastcontaining the deviations from each forecast for calculating forecast confidence intervals. The confidence level is specified inconfidence. Methodforecastmust be invoked before this method is called. Otherwise, anIllegalStateExceptionexception is thrown. By default,confidence= 0.95.
-
getForecast
public double[] getForecast()
Returns forecasts for the original outlier contaminated series.- Returns:
- a
doublearray of lengthnForecastcontaining the forecasts for the original series. Forecast origin is the time point of the last observed value in the time series,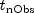 . Forecasts are
returned for lead times
. Forecasts are
returned for lead times 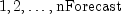 ,
i.e. time points
,
i.e. time points  .
Method
.
Method forecastmust be invoked before this method is called. Otherwise, anIllegalStateExceptionexception is thrown.
-
getMA
public double[] getMA()
Returns the final moving average parameter estimates of the optimum model. Note that one of thecomputemethods must be invoked first before invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.- Returns:
- a
doublearray containing the final moving average parameter estimates. If the optimum model has no MA component then a zero-length array is returned.
-
getNumberOfOutliers
public int getNumberOfOutliers()
Returns the number of outliers detected.- Returns:
- an
intscalar containing the number of outliers detected. Thecomputemethod must be invoked first before invoking this method. Otherwise, the method throws anIllegalStateExceptionexception.
-
getOptimumModelOrder
public int[] getOptimumModelOrder()
Returns the order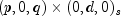 of the
optimum model. Note that one of the
of the
optimum model. Note that one of the computemethods must be invoked first before calling this method. Otherwise, anIllegalStateExceptionexception is thrown.- Returns:
- an
intarray of length 4 containing the values p, q, s and d for the optimum model.
-
getOutlierFreeForecast
public double[] getOutlierFreeForecast()
Returns forecasts for the outlier free series.- Returns:
- a
doublearray of lengthnForecastcontaining the forecasts for the outlier free series. Forecast origin is the time point of the last observed value in the time series,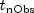 . Forecasts are
returned for lead times
. Forecasts are
returned for lead times 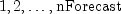 ,
i.e. time points
,
i.e. time points  . Method
. Method
forecastmust be invoked before this method is called. Otherwise, anIllegalStateExceptionexception is thrown.
-
getOutlierFreeSeries
public double[] getOutlierFreeSeries()
Returns the outlier free series.- Returns:
- a
doublearray containing the original time series with estimated missing values after removal of any outlier effects. One of thecomputemethods must be called before invoking this method. Otherwise, anIllegalStateExceptionexception is thrown.
-
getOutlierStatistics
public int[][] getOutlierStatistics()
Returns the outlier statistics.- Returns:
- a
doublearray of lengthnOutliersby 2, wherenOutliersis the number of detected outliers, containing the outlier statistics. The first column contains the time at which the outlier was observed (time ranging fromtimes[0]totimes[times.length - 1]) and the second column contains an identifier indicating the type of outlier observed. Outlier types fall into one of five categories:Identifier Outlier type INNOVATIONALInnovational Outliers (IO) ADDITIVEAdditive Outliers (AO) LEVEL_SHIFTLevel Shift Outliers (LS) TEMPORARY_CHANGETemporary Change Outliers (TC) UNABLE_TO_IDENTIFYUnable to Identify (UI) If the number of detected outliers equals zero, then an array of length zero is returned.
-
getPsiWeights
public double[] getPsiWeights()
Returns the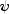 weights of the infinite order
moving average form of the model.
weights of the infinite order
moving average form of the model.- Returns:
- a
doublearray of lengthnForecastcontaining the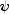 weights of the infinite
order moving average form of the optimum model for the outlier
free series. Method
weights of the infinite
order moving average form of the optimum model for the outlier
free series. Method forecastmust be invoked before this method is called. Otherwise, anIllegalStateExceptionexception is thrown.
-
getResiduals
public double[] getResiduals()
Returns the residuals. Note that one of thecomputemethods must be invoked first before invoking this method. Otherwise,getResidualsthrows anIllegalStateExceptionexception.- Returns:
- a
doublearray containing the residuals for the outlier and gap free series at the final parameter estimation point.
-
getResidualStandardError
public double getResidualStandardError()
Returns the residual standard error of the outlier free series. Note that one of thecomputemethods must be invoked first before calling this method. Otherwise, anIllegalStateExceptionexception is thrown.- Returns:
- a
doublescalar containing the standard error of the outlier free series.
-
setAccuracyTolerance
public void setAccuracyTolerance(double epsilon)
Sets the tolerance value controlling the accuracy of the parameter estimates.- Parameters:
epsilon- adoublescalar, a positive tolerance value controlling the accuracy of parameter estimates during outlier detection. Default:epsilon = 0.001.
-
setConfidence
public void setConfidence(double confidence)
Sets the confidence level for calculating confidence limit deviations returned bygetDeviations.- Parameters:
confidence- adoublescalar specifying the confidence level used in computing forecast confidence intervals. Typical choices forconfidenceare 0.90, 0.95, and 0.99.confidencemust be greater than 0.0 and less than 1.0. Default:confidence = 0.95.
-
setCriticalValue
public void setCriticalValue(double critical)
Sets the critical value used as a threshold during outlier detection.- Parameters:
critical- adoublescalar, the critical value used as a threshold for the statistics used in the outlier detection.criticalmust be greater than zero. Default:critical = 3.0.
-
setDelta
public void setDelta(double delta)
Sets the dampening effect parameter.- Parameters:
delta- adoublescalar, the dampening effect parameter used in the detection of a Temporary Change Outlier (TC).deltamust be greater than 0 and less than 1. Default:delta = 0.7.
-
setDifferenceOrders
public void setDifferenceOrders(int[] orders)
Defines the orders of the periodic differences used in the determination of the optimum model.- Parameters:
orders- anintarray containing all possible orders for each difference given inperiods. All elements inordersmust be non-negative. By default,ordersis a one-element array withorders[0]= 0.
-
setMaximumARLag
public void setMaximumARLag(int maxARLag)
Defines the maximum AR lag used in the determination of the optimum (s,d) combination of methodcompute(int[] arOrders, int[] maOrders).- Parameters:
maxARLag- a scalarint, the maximum AR lag used in the computation of the optimum (s,d) combination for methodcompute(int[] arOrders, int[] maOrders). It is required thatmaxARLagis greater than zero and smaller than the original series after replacement of potential missing values. By default,maxARLag= 10.
-
setModelSelectionCriterion
public void setModelSelectionCriterion(int infoCriterion)
Sets the model selection criterion.- Parameters:
infoCriterion- anintscalar indicating the model selection criterion used in the search for the optimum model.infoCriterion Model selection criterion AICAkaike's information criterion (AIC) AICCAkaike's corrected information criterion (AICC) BICBayesian information criterion (BIC) By default, AIC is chosen.
-
setPeriods
public void setPeriods(int[] periods)
Defines the periods used in the determination of the optimum model.- Parameters:
periods- anintarray containing all possible periods that can be applied to the original series after insertion of missing values. All elements ofperiodsmust be positive. By default,periodsis a one-element array withperiods[0]= 1;
-
setRelativeError
public void setRelativeError(double relativeError)
Sets the stopping criterion for use in the nonlinear equation solver.- Parameters:
relativeError- adoublepositive scalar containing the stopping criterion for use in the nonlinear equation solver used in the least-squares algorithm. Default:relativeError = 2.2204460492503131e-012.
-
-