- java.lang.Object
-
- com.imsl.stat.KalmanFilter
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class KalmanFilter extends Object implements Serializable, Cloneable
Performs Kalman filtering and evaluates the likelihood function for the state-space model.Class
KalmanFilteris based on a recursive algorithm given by Kalman (1960), which has come to be known as the Kalman filter. The underlying model is known as the state-space model. The model is specified stage by stage where the stages generally correspond to time points at which the observations become available.KalmanFilteravoids many of the computations and storage requirements that would be necessary if one were to process all the data at the end of each stage in order to estimate the state vector. This is accomplished by using previous computations and retaining in storage only those items essential for processing of future observations.The notation used here follows that of Sallas and Harville (1981). Let
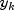 (input in
(input in yusing methodupdate) be the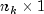 vector of
observations that become available at time k. The subscript k
is used here rather than t, which is more customary in time series,
to emphasize that the model is expressed in stages
vector of
observations that become available at time k. The subscript k
is used here rather than t, which is more customary in time series,
to emphasize that the model is expressed in stages
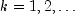 and that these stages need not
correspond to equally spaced time points. In fact, they need not correspond
to time points of any kind. The observation equation for the
state-space model is
and that these stages need not
correspond to equally spaced time points. In fact, they need not correspond
to time points of any kind. The observation equation for the
state-space model is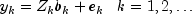
Here,
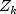 (input in
(input in zusing methodupdate) is an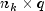 known matrix and
known matrix and
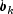 is the
is the 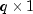 state vector. The
state vector
state vector. The
state vector 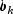 is allowed to change with time in
accordance with the state equation
is allowed to change with time in
accordance with the state equation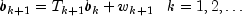
starting with
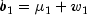 .
.The change in the state vector from time k to k + 1 is explained in part by the transition matrix
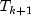 (the identity matrix
by default, or optionally using method
(the identity matrix
by default, or optionally using method setTransitionMatrix), which is assumed known. It is assumed that the q-dimensional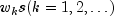 are independently distributed multivariate normal with mean vector 0 and
variance-covariance matrix
are independently distributed multivariate normal with mean vector 0 and
variance-covariance matrix 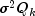 , that the
, that the
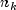 -dimensional
-dimensional 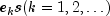 are independently distributed multivariate normal with mean vector 0 and
variance-covariance matrix
are independently distributed multivariate normal with mean vector 0 and
variance-covariance matrix 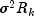 , and that the
, and that the
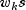 and
and 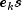 are independent of
each other. Here,
are independent of
each other. Here, 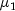 is the mean of
is the mean of
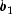 and is assumed known,
and is assumed known, 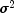 is an unknown positive scalar.
is an unknown positive scalar. 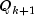 (input in
(input in
Q) and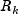 (input in
(input in R) are assumed known.Denote the estimator of the realization of the state vector
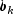 given the observations
given the observations
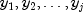 by
by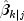
By definition, the mean squared error matrix for
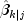
is
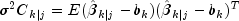
At the time of the k-th invocation, we have
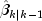
and
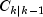 , which were computed
from the k-1-st invocation, input in
, which were computed
from the k-1-st invocation, input in bandcovb, respectively. During the k-th invocation,KalmanFiltercomputes the filtered estimate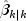
along with
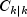 . These quantities
are given by the update equations:
. These quantities
are given by the update equations: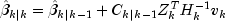
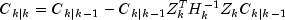
where
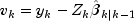
and where
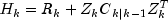
Here,
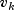 (stored in
(stored in getPredictionError) is the one-step-ahead prediction error, and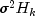 is the
variance-covariance matrix for
is the
variance-covariance matrix for 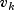 .
.
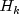 is obtained from method
is obtained from method getCovV. The "start-up values" needed on the first invocation ofKalmanFilterare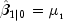
and
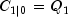 input via
input via
bandcovb, respectively. Computations for the k-th invocation are completed byKalmanFiltercomputing the one-step-ahead estimate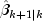
along with
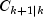 given by the
prediction equations:
given by the
prediction equations: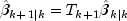
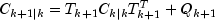
If both the filtered estimates and one-step-ahead estimates are needed by the user at each time point,
KalmanFiltercan be used twice for each time point-first without methodsSetTransitionMatrixandsetQto produce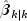
and
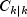 , and second without method
, and second without method
updateto produce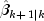
and
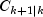 (Without methods
(Without methods
SetTransitionMatrixandsetQ, the prediction equations are skipped. Without methodupdate, the update equations are skipped.).Often, one desires the estimate of the state vector more than one-step-ahead, i.e., an estimate of
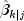
is needed where
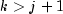 . At time j,
. At time j,
KalmanFilteris invoked with methodupdateto compute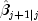
Subsequent invocations of
KalmanFilterwithout methodupdatecan compute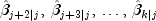
Computations for
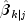
and
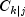 assume the
variance-covariance matrices of the errors in the observation equation and
state equation are known up to an unknown positive scalar multiplier,
assume the
variance-covariance matrices of the errors in the observation equation and
state equation are known up to an unknown positive scalar multiplier,
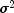 . The maximum likelihood estimate of
. The maximum likelihood estimate of
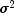 based on the observations
based on the observations
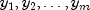 , is given by
, is given by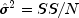
where
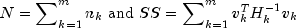
N and SS are input arguments
rankandSumofSquares. Updated values are obtained from methodsgetRankandgetSumofSquaresIf
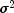 is known, the
is known, the 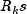 and
and 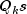 can be input as the variance-covariance
matrices exactly. The earlier discussion is then simplified by letting
can be input as the variance-covariance
matrices exactly. The earlier discussion is then simplified by letting
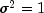 .
.In practice, the matrices
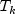 ,
,
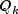 , and
, and 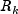 are
generally not completely known. They may be known functions of an unknown
parameter vector
are
generally not completely known. They may be known functions of an unknown
parameter vector 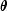 . In this case,
. In this case,
KalmanFiltercan be used in conjunction with an optimization class (seeMinUnconMultiVar, JMSL Math package), to obtain a maximum likelihood estimate of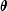 . The
natural logarithm of the likelihood function for
. The
natural logarithm of the likelihood function for
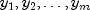 differs by no more than an
additive constant from
differs by no more than an
additive constant from![L(theta ,sigma ^2 ;y_1 ,y_2 ,; ldots
,;y_m ) = - frac{1}{2}N,{rm{ln}}, sigma ^{rm{2}} -
frac{1}{2}sumlimits_{k = 1}^m {{rm{ln}}[{rm{det}}(H_k )] -
frac{1}{2}sigma ^{ - 2} sumlimits_{k = 1}^m {v_k^T H_k^{ - 1}
v_k } }](eqn_2941.png)
(Harvey 1981, page 14, equation 2.21).
Here,
![sumnolimits_{k = 1}^m
{{rm{ln}}[{rm{det}}(H_k )]}](eqn_2942.png)
(input in
logDeterminant, updated bygetLogDeterminant) is the natural logarithm of the determinant of V where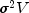 is the variance-covariance
matrix of the observations.
is the variance-covariance
matrix of the observations.Minimization of
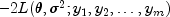 over all
over all 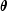 and
and 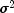 produces maximum likelihood estimates. Equivalently, minimization of
produces maximum likelihood estimates. Equivalently, minimization of
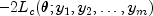 where
where![L_c (theta ;y_1 ,y_2 ,; ldots ,;y_m ) =
- frac{1}{2}N,{rm{ln}}left( {frac{{SS}}{N}} right) -
frac{1}{2}sumlimits_{k = 1}^m {{rm{ln}}[{rm{det}}(H_k )]}](eqn_2948.png)
produces maximum likelihood estimates
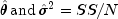
Minimization of
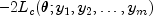 instead of
instead of 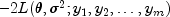 ,
reduces the dimension of the minimization problem by one. The two
optimization problems are equivalent since
,
reduces the dimension of the minimization problem by one. The two
optimization problems are equivalent since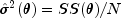
minimizes
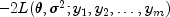 for all
for all 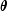 , consequently,
, consequently,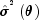
can be substituted for
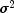 in
in
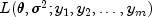 to give
a function that differs by no more than an additive constant from
to give
a function that differs by no more than an additive constant from
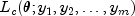 .
.The earlier discussion assumed
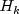 to be nonsingular.
If
to be nonsingular.
If 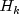 is singular, a modification for singular
distributions described by Rao (1973, pages 527-528) is used. The necessary
changes in the preceding discussion are as follows:
is singular, a modification for singular
distributions described by Rao (1973, pages 527-528) is used. The necessary
changes in the preceding discussion are as follows:- Replace
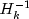 by a generalized inverse.
by a generalized inverse. - Replace
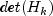 by the product of the nonzero
eigenvalues of
by the product of the nonzero
eigenvalues of 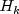 .
. - Replace N by
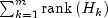
Maximum likelihood estimation of parameters in the Kalman filter is discussed by Sallas and Harville (1988) and Harvey (1981, pages 111-113).
- See Also:
- Example, Maximum Likelihood Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description KalmanFilter(double[] b, double[][] covb, int rank, double sumOfSquaress, double logDeterminant)Constructor forKalmanFilter.
-
Method Summary
Methods Modifier and Type Method and Description voidfilter()Performs Kalman filtering and evaluates the likelihood function for the state-space model.double[][]getCovB()Returns the mean squared error matrix forbdivided by sigma squared.double[][]getCovV()Returns the variance-covariance matrix of v divided by sigma squared.doublegetLogDeterminant()Returns the natural log of the product of the nonzero eigenvalues of P where P * sigma2 is the variance-covariance matrix of the observations.double[]getPredictionError()Returns the one-step-ahead prediction error.intgetRank()Returns the rank of the variance-covariance matrix for all the observations.double[]getStateVector()Returns the estimated state vector at time k + 1 given the observations through time k.doublegetSumOfSquares()Returns the generalized sum of squares.voidresetQ()Removes the Q matrix.voidresetTransitionMatrix()Removes the transition matrix.voidresetUpdate()Do not perform computation of the update equations.voidsetQ(double[][] q)Sets the Q matrix.voidsetTolerance(double tolerance)Sets the tolerance used in determining linear dependence.voidsetTransitionMatrix(double[][] t)Sets the transition matrix.voidupdate(double[] y, double[][] z, double[][] r)Performs computation of the update equations.
-
-
-
Constructor Detail
-
KalmanFilter
public KalmanFilter(double[] b, double[][] covb, int rank, double sumOfSquaress, double logDeterminant)Constructor forKalmanFilter.- Parameters:
b- Adoublearray containing the estimated state vector.bis the estimated state vector at timekgiven the observations through timek-1.covb- Adoublematrix of sizeb.lengthbyb.lengthsuch thatcovb*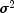 is
the mean squared error matrix for
is
the mean squared error matrix for b.rank- Anintscalar containing the rank of the variance-covariance matrix for all the observations.sumOfSquaress- Adoublescalar containing the generalized sum of squares.logDeterminant- Adoublescalar containing the natural log of the product of the nonzero eigenvalues of P whereP*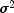 is the variance-covariance
matrix of the observations.
is the variance-covariance
matrix of the observations.- Throws:
IllegalArgumentException- is thrown if the dimensions ofb, andcovbare not consistent.
-
-
Method Detail
-
filter
public final void filter()
Performs Kalman filtering and evaluates the likelihood function for the state-space model.
-
getCovB
public double[][] getCovB()
Returns the mean squared error matrix forbdivided by sigma squared.- Returns:
- a
doublematrix of sizeb.lengthbyb.lengthsuch thatcovb*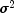 is the mean squared error
matrix for
is the mean squared error
matrix for b.
-
getCovV
public double[][] getCovV()
Returns the variance-covariance matrix of v divided by sigma squared.- Returns:
- a
doublematrix containing ay.length by y.lengthmatrix such thatcovv*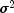 is the
variance-covariance matrix of the one-step-ahead prediction error,
is the
variance-covariance matrix of the one-step-ahead prediction error, getPredictionError.
-
getLogDeterminant
public double getLogDeterminant()
Returns the natural log of the product of the nonzero eigenvalues of P where P * sigma2 is the variance-covariance matrix of the observations.- Returns:
- a
doublescalar containing the natural log of the product of the nonzero eigenvalues of P whereP*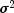 is the variance-covariance
matrix of the observations. In the usual case when P is
nonsingular,
is the variance-covariance
matrix of the observations. In the usual case when P is
nonsingular, logDeterminantis the natural log of the determinant of P.
-
getPredictionError
public double[] getPredictionError()
Returns the one-step-ahead prediction error.- Returns:
- a
doublearray of sizey.lengthcontaining the one-step-ahead prediction error.
-
getRank
public int getRank()
Returns the rank of the variance-covariance matrix for all the observations.- Returns:
- An
intscalar containing the rank of the variance-covariance matrix for all the observations.
-
getStateVector
public double[] getStateVector()
Returns the estimated state vector at time k + 1 given the observations through time k.- Returns:
- a
doublearray containing the estimated state vector at time k + 1 given the observations through time k.
-
getSumOfSquares
public double getSumOfSquares()
Returns the generalized sum of squares.- Returns:
- a
doublescalar containing the generalized sum of squares. The estimate of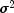 is given by
is given by
sumOfSquares / rank.
-
resetQ
public void resetQ()
Removes the Q matrix.
-
resetTransitionMatrix
public void resetTransitionMatrix()
Removes the transition matrix.
-
resetUpdate
public void resetUpdate()
Do not perform computation of the update equations.
-
setQ
public void setQ(double[][] q)
Sets the Q matrix.- Parameters:
q- Adoublematrix containing theb.length by b.lengthmatrix such thatq*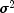 is the variance-covariance matrix of the
error vector in the state equation.
Default: There is no error term in the state equation.
is the variance-covariance matrix of the
error vector in the state equation.
Default: There is no error term in the state equation.
-
setTolerance
public void setTolerance(double tolerance)
Sets the tolerance used in determining linear dependence.- Parameters:
tolerance- Adoublescalar containing the tolerance used in determining linear dependence. Default:tolerance= 100.0*2.2204460492503131e-16.
-
setTransitionMatrix
public void setTransitionMatrix(double[][] t)
Sets the transition matrix.- Parameters:
t- Adoublematrix containing theb.length by b.lengthtransition matrix in the state equation. Default:t= identity matrix
-
update
public void update(double[] y, double[][] z, double[][] r)Performs computation of the update equations.- Parameters:
y- Adoublearray containing the observations.z- Adoublematrix containing they.length by b.lengthmatrix relating the observations to the state vector in the observation equation.r- Adoublematrix containing they.length by y.lengthmatrix such thatr*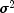 is the variance-covariance matrix of
errors in the observation equation.
is the variance-covariance matrix of
errors in the observation equation. 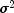 is a positive unknown scalar. Only elements in the upper
triangle of
is a positive unknown scalar. Only elements in the upper
triangle of rare referenced.
-
-