- java.lang.Object
-
- com.imsl.stat.KaplanMeierECDF
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class KaplanMeierECDF extends Object implements Serializable, Cloneable
Computes the Kaplan-Meier reliability function estimates or the CDF based on failure data that may be multi-censored.The Kaplan-Meier (K-M) Product Limit procedure provides simple estimates of the reliability function or the CDF based on failure data that may be multi-censored. No underlying probability model is assumed; K-M estimation is an empirical (non-parametric) procedure. Exact times of failure are required.
Consider a situation in which we are reliability testing n (non-repairable) units taken randomly from a population. We are investigating the population to determine if its failure rate is acceptable. In the typical test scenario, we have a fixed time T to run the units to see if they survive or fail. The data obtained are called Censored Type I data.
During the T hours of test we observe r failures (where r can be any number from 0 to n). The failure times are
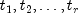 , and there are
, and there are 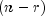 units
that survived the entire T-hour test without failing. Note that T
is fixed in advance, and r is an output of the testing, since we
don't know how many failures will occur until the test is run. Note that we
assume the exact times of failure are recorded when they occur.
units
that survived the entire T-hour test without failing. Note that T
is fixed in advance, and r is an output of the testing, since we
don't know how many failures will occur until the test is run. Note that we
assume the exact times of failure are recorded when they occur. This type of data is also called "right censored" data since the times of failure to the right (i.e., larger than T) are missing. The steps for calculating K-M estimates are the following:
- Order the actual failure times from
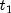 through
through
 , where there are r failures
, where there are r failures - Corresponding to each
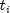 , associate the number
, associate the number
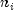 with
with 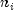 = the number of
operating units just before the ith failure occurred at time
= the number of
operating units just before the ith failure occurred at time
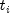
- First estimate the survival
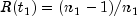
- Estimate each ensuing survival
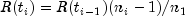 ,
, 
- Estimate the CDF
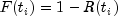 ,
, 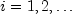
Note that non-failed units taken off testing (i.e., right-censored) only count up to the last actual failure time before they were removed. They are included in the
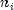 counts up to and including that
failure time, but not after.
counts up to and including that
failure time, but not after.- See Also:
- Example, Serialized Form
-
-
Constructor Summary
Constructors Constructor and Description KaplanMeierECDF(double[] t)Constructor forKaplanMeierECDF.
-
Method Summary
Methods Modifier and Type Method and Description double[]evaluateCDF()Computes the empirical CDF and returns the CDF values up to, but not including the time values returned bygetTimes.intgetNumberOfPoints()Retrieves the number of points in the empirical CDFdouble[]getTimes()Retrieves the time values where the step function CDF jumps to a greater value.voidsetCensor(int[] censor)Set flags to note right-censoringvoidsetFrequency(int[] freq)Sets the frequency for each entry int
-
-
-
Constructor Detail
-
KaplanMeierECDF
public KaplanMeierECDF(double[] t)
Constructor forKaplanMeierECDF.- Parameters:
t- adoublearray containing the failure times.
-
-
Method Detail
-
evaluateCDF
public double[] evaluateCDF()
Computes the empirical CDF and returns the CDF values up to, but not including the time values returned bygetTimes.- Returns:
- a
doublearray of CDF values.
-
getNumberOfPoints
public int getNumberOfPoints()
Retrieves the number of points in the empirical CDF- Returns:
- an
intcontaining the number of points in the empirical CDF. - Throws:
IllegalStateException- is thrown if the CDF has not been evaluated.
-
getTimes
public double[] getTimes()
Retrieves the time values where the step function CDF jumps to a greater value. This array has right-censored values oftremoved.- Returns:
- a
doublearray of time values. - Throws:
IllegalStateException- is thrown if the CDF has not been evaluated.
-
setCensor
public void setCensor(int[] censor)
Set flags to note right-censoring- Parameters:
censor- anintarray of 0 or 1 flags to note right-censoring. Values of 0 = continue to use datum and 1 = remove datum. If this method is not called, no data is right-censored.
-
setFrequency
public void setFrequency(int[] freq)
Sets the frequency for each entry int- Parameters:
freq- adoublearray containing the repeat count for each entry int.
-
-