- java.lang.Object
-
- com.imsl.stat.LinearRegression
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class LinearRegression extends Object implements Serializable, Cloneable
Fits a multiple linear regression model with or without an intercept. If the constructor argumenthasInterceptis true, the multiple linear regression model is
where the observed values of the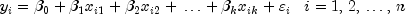
 's constitute the responses or values of the
dependent variable, the
's constitute the responses or values of the
dependent variable, the 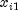 's,
's, 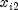 's,
's, 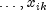 's are the settings of the
independent variables,
's are the settings of the
independent variables, 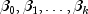 are the regression coefficients, and the
are the regression coefficients, and the 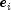 's are
independently distributed normal errors each with mean zero and variance
's are
independently distributed normal errors each with mean zero and variance
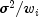 . If
. If hasInterceptisfalse,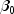 is not included in the model.
is not included in the model.
LinearRegressioncomputes estimates of the regression coefficients by minimizing the sum of squares of the deviations of the observed response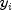 from the fitted response
from the fitted response 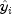
for the observations. This minimum sum of squares (the error sum of squares) is in the ANOVA output and denoted by
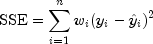
In addition, the total sum of squares is output in the ANOVA table. For the case,
hasInterceptis true; the total sum of squares is the sum of squares of the deviations of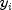 from its mean
from its mean
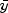
--the so-called corrected total sum of squares; it is denoted by
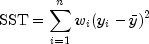
For the case
hasInterceptisfalse, the total sum of squares is the sum of squares of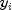 --the so-called
uncorrected total sum of squares; it is denoted by
--the so-called
uncorrected total sum of squares; it is denoted by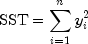
See Draper and Smith (1981) for a good general treatment of the multiple linear regression model, its analysis, and many examples.
In order to compute a least-squares solution,
LinearRegressionperforms an orthogonal reduction of the matrix of regressors to upper triangular form. Givens rotations are used to reduce the matrix. This method has the advantage that the loss of accuracy resulting from forming the crossproduct matrix used in the normal equations is avoided, while not requiring the storage of the full matrix of regressors. The method is described by Lawson and Hanson, pages 207-212.From a general linear model fitted using the
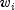 's as
the weights, inner class
's as
the weights, inner class LinearRegression.CaseStatisticscan also compute predicted values, confidence intervals, and diagnostics for detecting outliers and cases that greatly influence the fitted regression. Let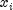 be a column vector containing elements of the
be a column vector containing elements of the
 -th row of
-th row of 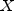 . Let
. Let 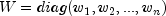 . The leverage is defined as
. The leverage is defined as
(In the case of linear equality restrictions on![h_i=[x_i^T(X^TWX)^-x_i]w_i](eqn_2704.png)
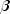 , the leverage is defined
in terms of the reduced model.) Put
, the leverage is defined
in terms of the reduced model.) Put 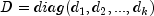 with
with 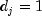 if the
if the  -th
diagonal element of
-th
diagonal element of 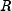 is positive and 0 otherwise. The
leverage is computed as
is positive and 0 otherwise. The
leverage is computed as 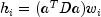 where
where
 is a solution to
is a solution to 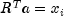 . The
estimated variance of
. The
estimated variance of
is given by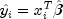
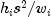 , where
, where 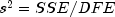 . The computation of the remainder of the case
statistics follows easily from their definitions.
. The computation of the remainder of the case
statistics follows easily from their definitions.
Let
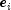 denote the residual
denote the residual
for the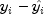
 th case. The
estimated variance of
th case. The
estimated variance of  is
is 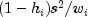 where
where  is the residual mean square
from the fitted regression. The
is the residual mean square
from the fitted regression. The  th standardized
residual (also called the internally studentized residual) is by definition
th standardized
residual (also called the internally studentized residual) is by definition
and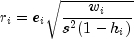
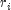 follows an approximate standard
normal distribution in large samples.
follows an approximate standard
normal distribution in large samples.
The
 th jackknife residual or deleted residual involves
the difference between
th jackknife residual or deleted residual involves
the difference between 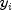 and its predicted value based
on the data set in which the
and its predicted value based
on the data set in which the  th case is deleted. This
difference equals
th case is deleted. This
difference equals 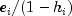 . The jackknife residual is
obtained by standardizing this difference. The residual mean square for the
regression in which the
. The jackknife residual is
obtained by standardizing this difference. The residual mean square for the
regression in which the  th case is deleted is
th case is deleted is
The jackknife residual is defined to be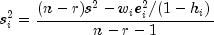
and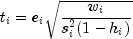
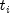 follows a
follows a  distribution with
distribution with 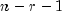 degrees of freedom.
degrees of freedom.
Cook's distance for the
 th case is a measure of how
much an individual case affects the estimated regression coefficients. It is
given by
th case is a measure of how
much an individual case affects the estimated regression coefficients. It is
given by
Weisberg (1985) states that if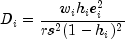
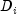 exceeds the 50-th percentile of the
exceeds the 50-th percentile of the 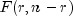 distribution, it should be considered large. (This value is about 1. This
statistic does not have an
distribution, it should be considered large. (This value is about 1. This
statistic does not have an 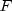 distribution.)
distribution.)
DFFITS, like Cook's distance, is also a measure of influence. For the
 th case, DFFITS is computed by the formula
th case, DFFITS is computed by the formula
Hoaglin and Welsch (1978) suggest that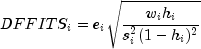
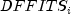 greater than
greater than
is large.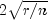
Often predicted values and confidence intervals are desired for combinations of settings of the effect variables not used in computing the regression fit. This can be accomplished using a single data matrix by including these settings of the variables as part of the data matrix and by setting the response equal to
Double.NaN.LinearRegressionwill omit the case when performing the fit and a predicted value and confidence interval for the missing response will be computed from the given settings of the effect variables.- See Also:
- Example1, Example2, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description classLinearRegression.CaseStatisticsInner ClassCaseStatisticsallows for the computation of predicted values, confidence intervals, and diagnostics for detecting outliers and cases that greatly influence the fitted regression.classLinearRegression.CoefficientTTestsContains statistics related to the regression coefficients.
-
Constructor Summary
Constructors Constructor and Description LinearRegression(int nVariables, boolean hasIntercept)Constructs a new linear regression object.
-
Method Summary
Methods Modifier and Type Method and Description ANOVAgetANOVA()Get an analysis of variance table and related statistics.LinearRegression.CaseStatisticsgetCaseStatistics(double[] x, double y)Returns the case statistics for an observation.LinearRegression.CaseStatisticsgetCaseStatistics(double[] x, double y, double w)Returns the case statistics for an observation and a weight.LinearRegression.CaseStatisticsgetCaseStatistics(double[] x, double y, double w, int pred)Returns the case statistics for an observation, weight, and future response count for the desired prediction interval.LinearRegression.CaseStatisticsgetCaseStatistics(double[] x, double y, int pred)Returns the case statistics for an observation and future response count for the desired prediction interval.double[]getCoefficients()Returns the regression coefficients.LinearRegression.CoefficientTTestsgetCoefficientTTests()Returns statistics relating to the regression coefficients.double[][]getR()Returns a copy of the R matrix.intgetRank()Returns the rank of the matrix.voidupdate(double[][] x, double[] y)Updates the regression object with a new set of observations.voidupdate(double[][] x, double[] y, double[] w)Updates the regression object with a new set of observations and weights.voidupdate(double[] x, double y)Updates the regression object with a new observation.voidupdate(double[] x, double y, double w)Updates the regression object with a new observation and weight.
-
-
-
Constructor Detail
-
LinearRegression
public LinearRegression(int nVariables, boolean hasIntercept)Constructs a new linear regression object.- Parameters:
nVariables-intnumber of variables in the regressionhasIntercept-booleanwhich indicates whether or not an intercept is in this regression model
-
-
Method Detail
-
getANOVA
public ANOVA getANOVA()
Get an analysis of variance table and related statistics.- Returns:
- an
ANOVAtable and related statistics
-
getCaseStatistics
public LinearRegression.CaseStatistics getCaseStatistics(double[] x, double y)
Returns the case statistics for an observation.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the LinearRegression constructor.y- adoublerepresenting the dependent (response) variable- Returns:
- the CaseStatistics for the observation.
-
getCaseStatistics
public LinearRegression.CaseStatistics getCaseStatistics(double[] x, double y, double w)
Returns the case statistics for an observation and a weight.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the constructor.y- adoublerepresenting the dependent (response) variablew- adoublerepresenting the weight- Returns:
- the CaseStatistics for the observation.
-
getCaseStatistics
public LinearRegression.CaseStatistics getCaseStatistics(double[] x, double y, double w, int pred)
Returns the case statistics for an observation, weight, and future response count for the desired prediction interval.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the constructor.y- adoublerepresenting the dependent (response) variablew- adoublerepresenting the weightpred- anintrepresenting the number of future responses for which the prediction interval is desired on the average of the future responses- Returns:
- the CaseStatistics for the observation.
-
getCaseStatistics
public LinearRegression.CaseStatistics getCaseStatistics(double[] x, double y, int pred)
Returns the case statistics for an observation and future response count for the desired prediction interval.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the constructor.y- adoublerepresenting the dependent (response) variablepred- anintrepresenting the number of future responses for which the prediction interval is desired on the average of the future responses.- Returns:
- the CaseStatistics for the observation.
-
getCoefficients
public double[] getCoefficients()
Returns the regression coefficients.- Returns:
- a
doublearray containing the regression coefficients. IfhasInterceptisfalseits length is equal to the number of variables. IfhasInterceptistruethen its length is the number of variables plus one and the 0-th entry is the value of the intercept. If the model is not full rank, the regression coefficients are not uniquely determined. In this case, a warning is issued and a solution with all linearly dependent regressors set to zero is returned. - See Also:
Warning
-
getCoefficientTTests
public LinearRegression.CoefficientTTests getCoefficientTTests()
Returns statistics relating to the regression coefficients.
-
getR
public double[][] getR()
Returns a copy of the R matrix. R is the upper triangular matrix containing the R matrix from a QR decomposition of the matrix of regressors.- Returns:
- a
doublematrix containing a copy of the R matrix
-
getRank
public int getRank()
Returns the rank of the matrix.- Returns:
- the
intrank of the matrix
-
update
public void update(double[][] x, double[] y)Updates the regression object with a new set of observations.- Parameters:
x- adoublematrix containing the independent (explanatory) variables. The number of rows inxmust equal the length ofyand the number of columns must be equal to the number of variables set in the constructor.y- adoublearray containing the dependent (response) variables.
-
update
public void update(double[][] x, double[] y, double[] w)Updates the regression object with a new set of observations and weights.- Parameters:
x- adoublematrix containing the independent (explanatory) variables. The number of rows inxmust equal the length ofyand the number of columns must be equal to the number of variables set in the constructor.y- adoublearray containing the dependent (response) variables.w- adoublearray representing the weights
-
update
public void update(double[] x, double y)Updates the regression object with a new observation.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the constructor.y- adoublerepresenting the dependent (response) variable
-
update
public void update(double[] x, double y, double w)Updates the regression object with a new observation and weight.- Parameters:
x- adoublearray containing the independent (explanatory) variables. Its length must be equal to the number of variables set in the constructor.y- adoublerepresenting the dependent (response) variablew- adoublerepresenting the weight
-
-