- java.lang.Object
-
- java.util.Random
-
- com.imsl.stat.Random
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class Random extends Random implements Serializable, Cloneable
Generate uniform and non-uniform random number distributions.The non-uniform distributions are generated from a uniform distribution. By default, this class uses the uniform distribution generated by the base class
Random. If the multiplier is set in this class then a multiplicative congruential method is used. The form of the generator is
Each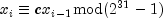
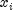 is then scaled into the unit interval (0,1). If
the multiplier, c, is a primitive root modulo
is then scaled into the unit interval (0,1). If
the multiplier, c, is a primitive root modulo
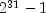 (which is a prime), then the generator will
have a maximal period of
(which is a prime), then the generator will
have a maximal period of  . There are several
other considerations, however. See Knuth (1981) for a good general
discussion. Possible values for c are 16807, 397204094, and 950706376.
The selection is made by the method
. There are several
other considerations, however. See Knuth (1981) for a good general
discussion. Possible values for c are 16807, 397204094, and 950706376.
The selection is made by the method
setMultiplier. Evidence suggests that the performance of 950706376 is best among these three choices (Fishman and Moore 1982).Alternatively, one can select a 32-bit or 64-bit Mersenne Twister generator by first instantiating
MersenneTwisterorMersenneTwister64. These generators have a period of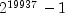 and a
623-dimensional equidistribution property. See Matsumoto et al. 1998 for
details.
and a
623-dimensional equidistribution property. See Matsumoto et al. 1998 for
details.The generation of uniform (0,1) numbers is done by the method
nextDouble.Nonuniform random numbers are generated using a variety of transformation procedures. All of the transformations used are exact (mathematically). The most straightforward transformation is the invers e CDF technique, but it is often less efficient than others involving acceptance/rejection and mixtures. See Kennedy and Gentle(1980) for discussion of these and other techniques.
Many of the nonuniform generators use different algorithms depending on the values of the parameters of the distributions. This is particularly true of the generators for discrete distributions. Schmeiser (1983) gives an overview of techniques for generating deviates from discrete distributions.Extensive empirical tests of some of the uniform random number generators available in the
Randomclass are reported by Fishman and Moore (1982 and 1986). Results of tests on the generator using the multiplier 16807 are reported by Learmonth and Lewis (1973). If the user wishes to perform additional tests, the routines in Chapter 17, Tests of Goodness of Fit, may be of use. Often in Monte Carlo applications, it is appropriate to construct an ad hoc test that is sensitive to departures that are important in the given application. For example, in using Monte Carlo methods to evaluate a one-dimensional integral, autocorrelations of order one may not be harmful, but they may be disastrous in evaluating a two-dimensional integral. Although generally the routines in this chapter for generating random deviates from nonuniform distributions use exact methods, and, hence, their quality depends almost solely on the quality of the underlying uniform generator, it is often advisable to employ an ad hoc test of goodness of fit for the transformations that are to be applied to the deviates from the nonuniform generator.Three methods are associated with copulas. A copula is a multivariate cumulative probability distribution (CDF) whose arguments are random variables uniformly distributed on the interval [0,1] corresponding to the probabilities (variates) associated with arbitrarily distributed marginal deviates. The copula structure allows the multivariate CDF to be partitioned into the copula, which has associated with it information characterizing the dependence among the marginal variables, and the set of separate marginal deviates, each of which has its own distribution structure.
Two methods,
nextGaussianCopulaandnextStudentsTCopula, allow the user to specify a correlation structure (in the form of a Cholesky matrix) which can be used to imprint correlation information on a sequence of multivariate random vectors. Each call to one of these methods returns a random vector whose elements (variates) are each uniformly distributed on the interval [0,1] and correlated according to a user-specified Cholesky matrix. These variate vector sequences may then be inverted to marginal deviate sequences whose distributions and imprinted correlations are user-specified.Method
nextGaussianCopulagenerates a random Gaussian copula sequence by inverting uniform [0,1] random numbers to N(0,1) deviates vectors, imprinting each vector with the correlation information by multiplying it with the Cholesky matrix, and then using the N(0,1) CDF to map the imprinted deviates back to uniform [0,1] variates.Method
nextStudentsTCopulainverts a vector of uniform [0, 1] random numbers to a N(0,1) deviate vector, imprints the vector with correlation information by multiplying it with the Cholesky matrix, transforms the imprinted N(0,1) vector to an imprinted Student's t vector (where each element is Student's t distributed with degrees of freedom) by dividing each element of the
imprinted N(0,1) vector by
degrees of freedom) by dividing each element of the
imprinted N(0,1) vector by 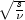 , where s is a random deviate taken from a chi-squared
distribution with
, where s is a random deviate taken from a chi-squared
distribution with
 degrees of freedom, and finally maps each element of
the resulting imprinted Student's t vector back to a uniform [0, 1]
distributed variate using the Student's t CDF.
degrees of freedom, and finally maps each element of
the resulting imprinted Student's t vector back to a uniform [0, 1]
distributed variate using the Student's t CDF.The third copula method,
canonicalCorrelation, extracts a correlation matrix from a sequence of multivariate deviate vectors whose component marginals are arbitrarily distributed. This is accomplished by first extracting the empirical CDF from each of the marginal deviates and then using this CDF to map the deviates to uniform [0,1] variates which are then inverted to Normal (0,1) deviates. Each element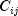 of the correlation matrix can then be extracted
by averaging the products
of the correlation matrix can then be extracted
by averaging the products 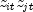 of deviates
i
and j over the t-indexed sequence. The utility of method
of deviates
i
and j over the t-indexed sequence. The utility of method
canonicalCorrelationis that because the correlation matrix is derived from N(0,1) deviates, the correlation is unbiased, i.e. undistorted by the arbitrary marginal distribution structures of the original deviate vector sequences. This is important in such financial applications as portfolio optimization, where correlation is used to estimate and minimize risk.The use of these routines is illustrated with RandomEx2.java, which first uses method
nextGaussianCopulato create a correlation imprinted sequence of random deviate vectors and then uses methodcanonicalCorrelationto extract the correlation matrix from the imprinted sequence of vectors.- See Also:
- Example 1, Example 2, Serialized Form
-
-
Nested Class Summary
Nested Classes Modifier and Type Class and Description static interfaceRandom.BaseGeneratorBase pseudorandom number.
-
Constructor Summary
Constructors Constructor and Description Random()Constructor for the Random number generator class.Random(long seed)Constructor for the Random number generator class with supplied seed.Random(Random.BaseGenerator baseGenerator)Constructor for the Random number generator class with an alternate basic number generator.
-
Method Summary
Methods Modifier and Type Method and Description double[][]canonicalCorrelation(double[][] deviate)MethodcanonicalCorrelationgenerates a canonical correlation matrix from an arbitrarily distributed multivariate deviate sequence withnvardeviate variables,nseqsteps in the sequence, and a Gaussian Copula dependence structure.protected intnext(int bits)Generates the next pseudorandom number.doublenextBeta(double p, double q)Generate a pseudorandom number from a beta distribution.intnextBinomial(int n, double p)Generate a pseudorandom number from a binomial distribution.doublenextCauchy()Generates a pseudorandom number from a Cauchy distribution.doublenextChiSquared(double df)Generates a pseudorandom number from a Chi-squared distribution.intnextDiscrete(int imin, double[] probabilities)Generate a pseudorandom number from a general discrete distribution using an alias method.doublenextExponential()Generates a pseudorandom number from a standard exponential distribution.doublenextExponentialMix(double theta1, double theta2, double p)Generate a pseudorandom number from a mixture of two exponential distributions.doublenextExtremeValue(double mu, double beta)Generate a pseudorandom number from an extreme value distribution.doublenextF(double dfn, double dfd)Generate a pseudorandom number from the F distribution.doublenextGamma(double a)Generates a pseudorandom number from a standard gamma distribution.double[]nextGaussianCopula(Cholesky chol)Generate pseudorandom numbers from a Gaussian Copula distribution.intnextGeometric(double p)Generate a pseudorandom number from a geometric distribution.intnextHypergeometric(int n, int m, int l)Generate a pseudorandom number from a hypergeometric distribution.intnextLogarithmic(double a)Generate a pseudorandom number from a logarithmic distribution.doublenextLogNormal(double mean, double stdev)Generate a pseudorandom number from a lognormal distribution.double[]nextMultivariateNormal(Cholesky matrix)Generate pseudorandom numbers from a multivariate normal distribution.intnextNegativeBinomial(double rk, double p)Generate a pseudorandom number from a negative binomial distribution.doublenextNormal()Generate a pseudorandom number from a standard normal distribution using an inverse CDF method.intnextPoisson(double theta)Generate a pseudorandom number from a Poisson distribution.doublenextRayleigh(double alpha)Generate a pseudorandom number from a Rayleigh distribution.doublenextStudentsT(double df)Generate a pseudorandom number from a Student's t distribution.double[]nextStudentsTCopula(double df, Cholesky chol)Generate pseudorandom numbers from a Student's t Copula distribution.doublenextTriangular()Generate a pseudorandom number from a triangular distribution on the interval (0,1).intnextUniformDiscrete(int k)Generate a pseudorandom number from a discrete uniform distribution.doublenextVonMises(double c)Generate a pseudorandom number from a von Mises distribution.doublenextWeibull(double a)Generate a pseudorandom number from a Weibull distribution.doublenextZigguratNormalAR()Generates pseudorandom numbers using the Ziggurat method.voidsetMultiplier(int multiplier)Sets the multiplier for a linear congruential random number generator.voidsetSeed(long seed)Sets the seed.voidskip(int n)Resets the seed to skip ahead in the base linear congruential generator.-
Methods inherited from class java.util.Random
nextBoolean, nextBytes, nextDouble, nextFloat, nextGaussian, nextInt, nextInt, nextLong
-
-
-
-
Constructor Detail
-
Random
public Random()
Constructor for the Random number generator class.
-
Random
public Random(long seed)
Constructor for the Random number generator class with supplied seed.- Parameters:
seed- alongwhich represents the random number generator seed in the range of -2,147,483,647 to +2,147,483,647
-
Random
public Random(Random.BaseGenerator baseGenerator)
Constructor for the Random number generator class with an alternate basic number generator.- Parameters:
baseGenerator- is used to override the methodnext.
-
-
Method Detail
-
canonicalCorrelation
public double[][] canonicalCorrelation(double[][] deviate)
Method
canonicalCorrelationgenerates a canonical correlation matrix from an arbitrarily distributed multivariate deviate sequence withnvardeviate variables,nseqsteps in the sequence, and a Gaussian Copula dependence structure.Method
canonicalCorrelationfirst maps each of thej=1..nvarinput deviate sequencesdeviate[k=1..nseq][j]into a corresponding sequence of variates, sayvariate[k][j](where variates are values of the empirical cumulative probability function,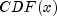 , defined as the probability that random
deviate variable
, defined as the probability that random
deviate variable  , and where
, and where
nseq = deviate.lengthandnvar = deviate[0].length). The variate matrixvariate[k][j]is then mapped into Normal(0,1) distributed deviates using the method
using the method
Cdf.inverseNormal(variate[k][j])and then the standard covariance estimator
is used to calculate the canonical correlation matrix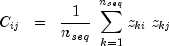
correlation = canonicalCorrelation(deviate), where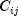 =
= correlation[i][j]and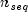 =
= nseq.If a multivariate distribution has Gaussian marginal distributions, then the standard "empirical" correlation matrix given above is "unbiased", i.e. an accurate measure of dependence among the variables. But when the marginal distributions depart significantly from Gaussian, i.e. are skewed or flattened, then the empirical correlation may become biased. One way to remove such bias from dependence measures is to map the non-Gaussian-distributed marginal deviates to Gaussian N(0,1) deviates (by mapping the non-Gaussian marginal deviates to empirically derived marginal CDF variate values, then inverting the variates to N(0,1) deviates as described above), and calculating the standard empirical correlation matrix from these N(0,1) deviates as in the equation above. The resulting "(Gaussian) canonical correlation" matrix thereby avoids the bias that would occur if the empirical correlation matrix were extracted from the non-Gaussian marginal distributions directly.
The canonical correlation matrix may be of value in such applications as Markowitz porfolio optimization, where an unbiased measure of dependence is required to evaluate portfolio risk, defined in terms of the portfolio variance which is in turn defined in terms of the correlation among the component portfolio instruments.
The utility of the canonical correlation derives from the observation that a "copula" multivariate distribution with uniformly-distributed deviates (corresponding to the CDF probabilities associated with the marginal deviates) may be mapped to arbitrarily distributed marginals, so that an unbiased dependence estimator derived from one set of marginals (N(0,1) distributed marginals) can be used to represent the dependence associated with arbitrarily-distributed marginals. The "Gaussian Copula" (whose variate arguments are derived from N(0,1) marginal deviates) is a particularly useful structure for representing multivariate dependence.
This is demonstrated in Example 2 where method
Random.nextGaussianCopula(CholeskyMtrx)(whereCholeskyMtrxis a Cholesky object derived from a user-specified covariance matrix) is used to imprint correlation information on otherwise arbitrarily distributed and independent random sequences. MethodRandom.canonicalCorrelationis then used to extract an unbiased correlation matrix from these imprinted deviate sequences.- Parameters:
deviate- is the doublenseqbynvararray of input deviate values.- See Also:
- Example
-
next
protected int next(int bits)
Generates the next pseudorandom number. If an alternate base generator was set in the constructor, itsnextmethod is used. If themultiplieris set then the multiplicative congruential method is used. Otherwise,super.next(bits)is used.
-
nextBeta
public double nextBeta(double p, double q)Generate a pseudorandom number from a beta distribution.Method
nextBetagenerates pseudorandom numbers from a beta distribution with parameters p and q, both of which must be positive. The probability density function is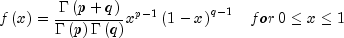
where
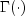 is the gamma function.
is the gamma function.The algorithm used depends on the values of p and q. Except for the trivial cases of p = 1 or q = 1, in which the inverse CDF method is used, all of the methods use acceptance/rejection. If p and q are both less than 1, the method of Johnk (1964) is used; if either p or q is less than 1 and the other is greater than 1, the method of Atkinson (1979) is used; if both p and q are greater than 1, algorithm BB of Cheng (1978), which requires very little setup time, is used.
The value returned is less than 1.0 and greater than
 , where
, where  is the smallest positive number such that
is the smallest positive number such that 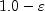 is less than 1.0.
is less than 1.0.- Parameters:
p- adouble, the first beta distribution parameter, p 0
0q- adouble, the second beta distribution parameter, q 0
0- Returns:
- a
double, a pseudorandom number from a beta distribution - See Also:
- Example
-
nextBinomial
public int nextBinomial(int n, double p)Generate a pseudorandom number from a binomial distribution.nextBinomialgenerates pseudorandom numbers from a binomial distribution with parameters n and p. n and p must be positive, and p must be less than 1. The probability function (with n = n and p = p) is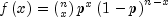
for
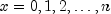 .
.The algorithm used depends on the values of n and p. If
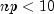 or if
p is less than a machine epsilon, the inverse CDF technique is
used; otherwise, the BTPE algorithm of Kachitvichyanukul and Schmeiser
(see Kachitvichyanukul 1982) is used. This is an acceptance/rejection
method using a composition of four regions. (TPE equals Triangle,
Parallelogram, Exponential, left and right.)
or if
p is less than a machine epsilon, the inverse CDF technique is
used; otherwise, the BTPE algorithm of Kachitvichyanukul and Schmeiser
(see Kachitvichyanukul 1982) is used. This is an acceptance/rejection
method using a composition of four regions. (TPE equals Triangle,
Parallelogram, Exponential, left and right.)- Parameters:
n- anint, the number of Bernoulli trials.p- adouble, the probability of success on each trial,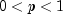 .
.- Returns:
- an
int, the pseudorandom number from a binomial distribution. - See Also:
- Example
-
nextCauchy
public double nextCauchy()
Generates a pseudorandom number from a Cauchy distribution. The probability density function is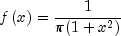
Use of the inverse CDF technique would yield a Cauchy deviate from a uniform (0, 1) deviate, u, as
![tan left[ {pi left( {u - .5} right)}right]](eqn_2274.png) .
Rather than evaluating a tangent directly, however,
.
Rather than evaluating a tangent directly, however,
nextCauchygenerates two uniform (-1, 1) deviates,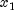 and
and 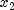 . These values can
be thought of as sine and cosine values. If
. These values can
be thought of as sine and cosine values. If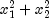
is less than or equal to 1, then
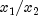 is delivered as the Cauchy deviate;
otherwise,
is delivered as the Cauchy deviate;
otherwise, 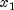 and
and 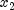 are
rejected and two new uniform (-1, 1) deviates are generated. This method
is also equivalent to taking the ratio of two independent normal
deviates.
are
rejected and two new uniform (-1, 1) deviates are generated. This method
is also equivalent to taking the ratio of two independent normal
deviates.Deviates from the Cauchy distribution with median t and first quartile t - s, that is, with density
![fleft( x right) = frac{s}{{pi left[ {s^2 +
left( {x - t} right)^2 } right]}}](eqn_2281.png)
can be obtained by scaling the output from
nextCauchy. To do this, first scale the output fromnextCauchyby S and then add T to the result.- Returns:
- a
double, a pseudorandom number from a Cauchy distribution - See Also:
- Example
-
nextChiSquared
public double nextChiSquared(double df)
Generates a pseudorandom number from a Chi-squared distribution.nextChiSquaredgenerates pseudorandom numbers from a chi-squared distribution withdfdegrees of freedom. Ifdfis an even integer less than 17, the chi-squared deviate r is generated as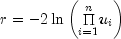
where
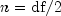 and the
and the
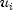 are independent random deviates from a uniform
(0, 1) distribution. If
are independent random deviates from a uniform
(0, 1) distribution. If dfis an odd integer less than 17, the chi-squared deviate is generated in the same way, except the square of a normal deviate is added to the expression above. Ifdfis greater than 16 or is not an integer, and if it is not too large to cause overflow in the gamma random number generator, the chi-squared deviate is generated as a special case of a gamma deviate, usingnextGamma. If overflow would occur innextGamma, the chi-squared deviate is generated in the manner described above, using the logarithm of the product of uniforms, but scaling the quantities to prevent underflow and overflow.- Parameters:
df- adoublewhich specifies the number of degrees of freedom. It must be positive.- Returns:
- a
double, a pseudorandom number from a Chi-squared distribution. - See Also:
- Example
-
nextDiscrete
public int nextDiscrete(int imin, double[] probabilities)Generate a pseudorandom number from a general discrete distribution using an alias method.Method
nextDiscretegenerates a pseudorandom number from a discrete distribution with probability function given in the vectorprobabilities; that is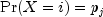
for
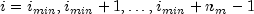 , where
, where
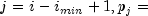
probabilities[j-1],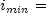
imin,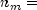
nmassandprobabilities.lengthis the number of mass points.The algorithm is the alias method, due to Walker (1974), with modifications suggested by Kronmal and Peterson (1979). On the first call with a set of probabilities, the method performs an initial setup after which the number generation phase is very fast. To increase efficiency, the code skips the setup phase on subsequent calls with the same inputs.
- Parameters:
imin- anintwhich specifies the smallest value the random deviate can assume. This is the value corresponding to the probability inprobabilities[0].probabilities- adoublearray containing the probabilities associated with the individual mass points. The elements ofprobabilitiesmust be nonnegative and must sum to 1.0. The length ofprobabilitiesmuse be greater than 1.- Returns:
- an
intwhich contains the random discrete deviate. - See Also:
- Example
-
nextExponential
public double nextExponential()
Generates a pseudorandom number from a standard exponential distribution. The probability density function is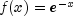 ;
for
;
for 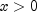 .
.
nextExponentialuses an antithetic inverse CDF technique; that is, a uniform random deviate U is generated and the inverse of the exponential cumulative distribution function is evaluated at 1.0 - U to yield the exponential deviate.Deviates from the exponential distribution with mean
 can be generated by using
can be generated by using
nextExponentialand then multiplying the result by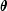 .
.- Returns:
- a
doublewhich specifies a pseudorandom number from a standard exponential distribution - See Also:
- Example
-
nextExponentialMix
public double nextExponentialMix(double theta1, double theta2, double p)Generate a pseudorandom number from a mixture of two exponential distributions. The probability density function is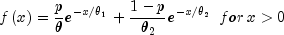
where
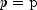 ,
,  , and
, and 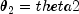 .
.In the case of a convex mixture, that is, the case
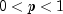 , the mixing parameter p is interpretable as a
probability; and
, the mixing parameter p is interpretable as a
probability; and nextExponentialMixwith probability p generates an exponential deviate with mean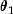 , and with probability
1 - p generates an exponential with mean
, and with probability
1 - p generates an exponential with mean
 . When p is greater than 1, but less
than
. When p is greater than 1, but less
than 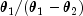 , then either an
exponential deviate with mean
, then either an
exponential deviate with mean 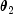 or the sum of two exponentials with means
or the sum of two exponentials with means  and
and  is generated. The probabilities are
is generated. The probabilities are
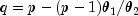 and
1 - q, respectively, for the single exponential and the sum of the
two exponentials.
and
1 - q, respectively, for the single exponential and the sum of the
two exponentials.- Parameters:
theta1- adoublewhich specifies the mean of the exponential distribution that has the larger mean.theta2- adoublewhich specifies the mean of the exponential distribution that has the smaller mean.theta2must be positive and less than or equal totheta1.p- adoublewhich specifies the mixing parameter. It must satisfy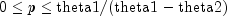 .
.- Returns:
- a
double, a pseudorandom number from a mixture of the two exponential distributions. - See Also:
- Example
-
nextExtremeValue
public double nextExtremeValue(double mu, double beta)Generate a pseudorandom number from an extreme value distribution.- Parameters:
mu- adoublescalar value representing the location parameter.beta- adoublescalar value representing the scale parameter.- Returns:
- a
doublepseudorandom number from an extreme value distribution - See Also:
- Example
-
nextF
public double nextF(double dfn, double dfd)Generate a pseudorandom number from the F distribution.- Parameters:
dfn- adouble, the numerator degrees of freedom. It must be positive.dfd- adouble, the denominator degrees of freedom. It must be positive.- Returns:
- a
double, a pseudorandom number from an F distribution - See Also:
- Example
-
nextGamma
public double nextGamma(double a)
Generates a pseudorandom number from a standard gamma distribution.Method
nextGammagenerates pseudorandom numbers from a gamma distribution with shape parameter a. The probability density function is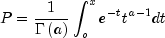
Various computational algorithms are used depending on the value of the shape parameter a. For the special case of a = 0.5, squared and halved normal deviates are used; and for the special case of a = 1.0, exponential deviates (from method
nextExponential) are used. Otherwise, if a is less than 1.0, an acceptance-rejection method due to Ahrens, described in Ahrens and Dieter (1974), is used; if a is greater than 1.0, a ten-region rejection procedure developed by Schmeiser and Lal (1980) is used.The Erlang distribution is a standard gamma distribution with the shape parameter having a value equal to a positive integer; hence,
nextGammagenerates pseudorandom deviates from an Erlang distribution with no modifications required.- Parameters:
a- adouble, the shape parameter of the gamma distribution. It must be positive.- Returns:
- a
double, a pseudorandom number from a standard gamma distribution - See Also:
- Example
-
nextGaussianCopula
public double[] nextGaussianCopula(Cholesky chol)
Generate pseudorandom numbers from a Gaussian Copula distribution.nextGaussianCopulagenerates pseudorandom numbers from a multivariate Gaussian Copula distribution which are uniformly distributed on the interval (0,1) representing the probabilities associated with N(0,1) deviates imprinted with correlation information from input Cholesky objectchol. Cholesky matrixRis defined as the "square root" of a user-defined correlation matrix, that isRis a lower triangular matrix such thatRtimes the transpose ofRis the correlation matrix. First, a length k vector of independent random normal deviates with mean 0 and variance 1 is generated, and then this deviate vector is pre-multiplied by Cholesky matrixR. Finally, the Cholesky-imprinted random N(0,1) deviates are mapped to output probabilities using the N(0,1) cumulative distribution function (CDF).Random deviates from arbitrary marginal distributions which are imprinted with the correlation information contained in Cholesky matrix
Rcan then be generated by inverting the output probabilities using user-specified inverse CDF functions.- Parameters:
chol- is theCholeskyobject containing the Cholesky factorization of the correlation matrix of order k.- Returns:
- a
doublearray which contains the pseudorandom numbers from a multivariate Gaussian Copula distribution. - See Also:
- Example 2
-
nextGeometric
public int nextGeometric(double p)
Generate a pseudorandom number from a geometric distribution.nextGeometricgenerates pseudorandom numbers from a geometric distribution with parameter p, where P =p is the probability of getting a success on any trial. A geometric deviate can be interpreted as the number of trials until the first success (including the trial in which the first success is obtained). The probability function is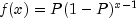
for
.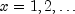 and
and
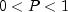
The geometric distribution as defined above has mean 1/P.
The i-th geometric deviate is generated as the smallest integer not less than
 , where the
, where the
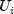 are independent uniform (0, 1) random numbers
(see Knuth, 1981).
are independent uniform (0, 1) random numbers
(see Knuth, 1981).The geometric distribution is often defined on 0, 1, 2, ..., with mean (1 - P)/P. Such deviates can be obtained by subtracting 1 from each element returned value.
- Parameters:
p- adouble, the probability of success on each trial,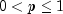 .
.- Returns:
- an
int, a pseudorandom number from a geometric distribution. - See Also:
- Example
-
nextHypergeometric
public int nextHypergeometric(int n, int m, int l)Generate a pseudorandom number from a hypergeometric distribution.Method
nextHypergeometricgenerates pseudorandom numbers from a hypergeometric distribution with parameters n, m, and l. The hypergeometric random variable x can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is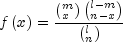
for
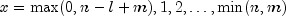 .
.If the
hypergeometricprobability function with parameters n, m, and l evaluated at n - l + m (or at 0 if this is negative) is greater than the machine epsilon, and less than 1.0 minus the machine epsilon, thennextHypergeometricuses the inverse CDF technique. The method recursively computes thehypergeometricprobabilities, starting at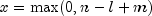 and using the ratio f (x = x + 1)/f(x = x) (see Fishman 1978, page
457).
and using the ratio f (x = x + 1)/f(x = x) (see Fishman 1978, page
457).If the
hypergeometricprobability function is too small or too close to 1.0, thennextHypergeometricgenerates integer deviates uniformly in the interval![[1, l- i]](eqn_2295.png) , for
, for
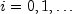 ; and at the I-th step, if
the generated deviate is less than or equal to the number of special
items remaining in the lot, the occurrence of one special item is tallied
and the number of remaining special items is decreased by one. This
process continues until the sample size or the number of special items in
the lot is reached, whichever comes first. This method can be much slower
than the inverse CDF technique. The timing depends on n. If
n is more than half of l
(which in practical examples is rarely the case), the user may wish to
modify the problem, replacing n by
l - n, and to consider the deviates to be the number of special
items not included in the sample.
; and at the I-th step, if
the generated deviate is less than or equal to the number of special
items remaining in the lot, the occurrence of one special item is tallied
and the number of remaining special items is decreased by one. This
process continues until the sample size or the number of special items in
the lot is reached, whichever comes first. This method can be much slower
than the inverse CDF technique. The timing depends on n. If
n is more than half of l
(which in practical examples is rarely the case), the user may wish to
modify the problem, replacing n by
l - n, and to consider the deviates to be the number of special
items not included in the sample.- Parameters:
n- anintwhich specifies the number of items in the sample, n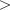 0
0m- anintwhich specifies the number of special items in the population, or lot, m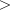 0
0l- anintwhich specifies the number of items in the lot, l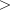 max(n,m)
max(n,m)- Returns:
- an
intwhich specifies the number of special items in a sample of size n drawn without replacement from a population of size l that contains m such special items. - See Also:
- Example
-
nextLogarithmic
public int nextLogarithmic(double a)
Generate a pseudorandom number from a logarithmic distribution.Method
nextLogarithmicgenerates pseudorandom numbers from a logarithmic distribution with parameter a. The probability function is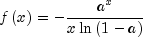
for
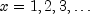 , and
, and
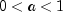 .
.The methods used are described by Kemp (1981) and depend on the value of a. If a is less than 0.95, Kemp's algorithm LS, which is a "chop-down" variant of an inverse CDF technique, is used. Otherwise, Kemp's algorithm LK, which gives special treatment to the highly probable values of 1 and 2, is used.
- Parameters:
a- adoublewhich specifies the parameter of the logarithmic distribution,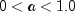 .
.- Returns:
- an
int, a pseudorandom number from a logarithmic distribution. - See Also:
- Example
-
nextLogNormal
public double nextLogNormal(double mean, double stdev)Generate a pseudorandom number from a lognormal distribution.Method
nextLogNormalgenerates pseudorandom numbers from a lognormal distribution with parametersmeanandstdev. The scale parameter in the underlying normal distribution,stdev, must be positive. The method is to generate normal deviates with meanmeanand standard deviationstdevand then to exponentiate the normal deviates.With
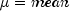 and
and  , the probability density function for the lognormal
distribution is
, the probability density function for the lognormal
distribution is![fleft( x right) = frac{1}{{sigma xsqrt
{2pi } }}exp left[ { - frac{1}{{2sigma ^2 }}left( {ln x - mu }
right)^2 } right],,for,x > 0](eqn_2341.png)
The mean and variance of the lognormal distribution are
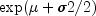 and
and
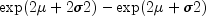 ,
respectively.
,
respectively.- Parameters:
mean- adoublewhich specifies the mean of the underlying normal distributionstdev- adoublewhich specifies the standard deviation of the underlying normal distribution. It must be positive.- Returns:
- a
double, a pseudorandom number from a lognormal distribution - See Also:
- Example
-
nextMultivariateNormal
public double[] nextMultivariateNormal(Cholesky matrix)
Generate pseudorandom numbers from a multivariate normal distribution.nextMultivariateNormalgenerates pseudorandom numbers from a multivariate normal distribution with mean vector consisting of all zeroes and variance-covariance matrix whose Cholesky factor (or "square root") ismatrix; that is,matrixis a lower triangular matrix such thatmatrixtimes the transpose ofmatrixis the variance-covariance matrix. First, independent random normal deviates with mean 0 and variance 1 are generated, and then the matrix containing these deviates is pre-multiplied bymatrix.Deviates from a multivariate normal distribution with means other than zero can be generated by using
nextMultivariateNormaland then by adding the means to the deviates.- Parameters:
matrix- is theCholeskyfactorization of the variance-covariance matrix of order k.- Returns:
- a
doublearray which contains the pseudorandom numbers from a multivariate normal distribution - See Also:
- Example
-
nextNegativeBinomial
public int nextNegativeBinomial(double rk, double p)Generate a pseudorandom number from a negative binomial distribution.Method
nextNegativeBinomialgenerates pseudorandom numbers from a negative binomial distribution with parameters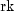 and
and 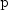 .
.
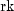 and
and 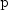 must be
positive and p must be less than 1. The probability function with
(
must be
positive and p must be less than 1. The probability function with
(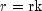 and
and
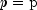 ) is
) is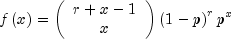
for
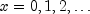 .
.If r is an integer, the distribution is often called the Pascal distribution and can be thought of as modeling the length of a sequence of Bernoulli trials until r successes are obtained, where p is the probability of getting a success on any trial. In this form, the random variable takes values r, r + 1,
 and can be obtained from the negative
binomial random variable defined above by adding r
to the negative binomial variable. This latter form is also equivalent to
the sum of r geometric random variables defined as taking values
and can be obtained from the negative
binomial random variable defined above by adding r
to the negative binomial variable. This latter form is also equivalent to
the sum of r geometric random variables defined as taking values
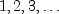 .
.If rp/(1 - p) is less than 100 and
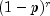 is greater than the machine epsilon,
is greater than the machine epsilon, nextNegativeBinomialuses the inverse CDF technique; otherwise, for each negative binomial deviate,nextNegativeBinomialgenerates a gamma (r, p/(1 - p)) deviate y and then generates a Poisson deviate with parameter y.- Parameters:
rk- adoublewhich specifies the negative binomial parameter, rk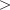 0
0p- adoublewhich specifies the probability of success on each trial. It must be greater than machine precision and less than one.- Returns:
- an
intwhich specifies the pseudorandom number from a negative binomial distribution. If rk is an integer, the deviate can be thought of as the number of failures in a sequence of Bernoulli trials before rk successes occur. - See Also:
- Example
-
nextNormal
public double nextNormal()
Generate a pseudorandom number from a standard normal distribution using an inverse CDF method. In this method, a uniform (0,1) random deviate is generated, then the inverse of the normal distribution function is evaluated at that point usinginverseNormal. This method is slower than the acceptance/rejection technique used in thenextNormalARto generate standard normal deviates. Deviates from the normal distribution with mean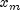 and
standard deviation
and
standard deviation
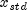 can be obtained by scaling the output from
can be obtained by scaling the output from
nextNormal. To do this first scale the output ofnextNormalby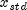 and then add
and then add
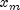 to the result.
to the result.- Returns:
- a
doublewhich represents a pseudorandom number from a standard normal distribution - See Also:
- Example
-
nextPoisson
public int nextPoisson(double theta)
Generate a pseudorandom number from a Poisson distribution.Method
nextPoissongenerates pseudorandom numbers from a Poisson distribution with parametertheta.theta, which is the mean of the Poisson random variable, must be positive. The probability function (with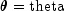 ) is
) is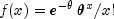
for
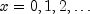
If
thetais less than 15,nextPoissonuses an inverse CDF method; otherwise thePTPEmethod of Schmeiser and Kachitvichyanukul (1981) (see also Schmeiser 1983) is used.The
PTPEmethod uses a composition of four regions, a triangle, a parallelogram, and two negative exponentials. In each region except the triangle, acceptance/rejection is used. The execution time of the method is essentially insensitive to the mean of the Poisson.- Parameters:
theta- adoublewhich specifies the mean of the Poisson distribution, theta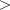 0
0- Returns:
- an
int, a pseudorandom number from a Poisson distribution - See Also:
- Example
-
nextRayleigh
public double nextRayleigh(double alpha)
Generate a pseudorandom number from a Rayleigh distribution.Method
nextRayleighgenerates pseudorandom numbers from a Rayleigh distribution with scale parameter alpha.- Parameters:
alpha- adoublewhich specifies the scale parameter of the Rayleigh distribution- Returns:
- a
double, a pseudorandom number from a Rayleigh distribution - See Also:
- Example
-
nextStudentsT
public double nextStudentsT(double df)
Generate a pseudorandom number from a Student's t distribution.nextStudentsTgenerates pseudo-random numbers from a Student's t distribution withdfdegrees of freedom, using a method suggested by Kinderman, Monahan, and Ramage (1977). The method ("TMX" in the reference) involves a representation of the t density as the sum of a triangular density over (-2, 2) and the difference of this and the t density. The mixing probabilities depend on the degrees of freedom of the t distribution. If the triangular density is chosen, the variate is generated as the sum of two uniforms; otherwise, an acceptance/rejection method is used to generate a variate from the difference density.For degrees of freedom less than 100,
nextStudentsTrequires approximately twice the execution time asnextNormalAR, which generates pseudorandom normal deviates. The execution time ofnextStudentsTincreases very slowly as the degrees of freedom increase. Since for very large degrees of freedom the normal distribution and the t distribution are very similar, the user may find that the difference in the normal and the t does not warrant the additional generation time required to usenextStudentsTinstead ofnextNormalAR.- Parameters:
df- adoublewhich specifies the number of degrees of freedom. It must be positive.- Returns:
- a
double, a pseudorandom number from a Student's t distribution - See Also:
- Example
-
nextStudentsTCopula
public double[] nextStudentsTCopula(double df, Cholesky chol)Generate pseudorandom numbers from a Student's t Copula distribution.nextStudentsTCopulagenerates pseudorandom numbers from a multivariate Student's t Copula distribution which are uniformly distributed on the interval (0,1) representing the probabilities associated with Student's t deviates withdfdegrees of freedom imprinted with correlation information from the input Cholesky objectchol. Cholesky matrixRis defined as the "square root" of a user-defined correlation matrix, i.e.Ris a lower triangular matrix such thatRtimes the transpose ofRis the correlation matrix. First, a length k vector of independent random normal deviates with mean 0 and variance 1 is generated, and then this deviate vector is pre-multiplied by Cholesky matrixR. Each of the k elements of the resulting vector of Cholesky-imprinted random deviates is then divided by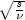 , where
, where
 =
= dfand s is a random deviate taken from a chi-squared distribution withdfdegrees of freedom. Each element of the Cholesky-imprinted N(0,1) vector is a linear combination of normally distributed random numbers and is therefore itself normal, and the division of each element by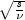 therefore insures that each element of the resulting vector
is Student's t distributed. Finally each element of the
Cholesky-imprinted Student's t vector is mapped to an output
probability using the Student's t cumulative distribution function
(CDF) with
therefore insures that each element of the resulting vector
is Student's t distributed. Finally each element of the
Cholesky-imprinted Student's t vector is mapped to an output
probability using the Student's t cumulative distribution function
(CDF) with dfdegrees of freedom.Random deviates from arbitrary marginal distributions which are imprinted with the correlation information contained in Cholesky matrix
Rcan then be generated by inverting the output probabilities using user-specified inverse CDF functions.- Parameters:
df- adoublewhich specifies the degrees of freedom parameter.chol- theCholeskyobject containing the Cholesky factorization of the correlation matrix of order k.- Returns:
- a
doublearray which contains the pseudorandom numbers from a multivariate Students t Copula distribution withdfdegrees of freedom.
-
nextTriangular
public double nextTriangular()
Generate a pseudorandom number from a triangular distribution on the interval (0,1). The probability density function is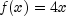 , for
, for 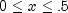 ,
and
,
and 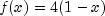 , for
, for
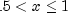 .
. nextTriangularuses an inverse CDF technique.- Returns:
- a
double, a pseudorandom number from a triangular distribution on the interval (0,1) - See Also:
- Example
-
nextUniformDiscrete
public int nextUniformDiscrete(int k)
Generate a pseudorandom number from a discrete uniform distribution.nextUniformDiscretegenerates pseudorandom numbers from a discrete uniform distribution with parameter k. The integers occur with equal probability. A random integer is generated by
multiplying
k by a uniform (0,1) random number, adding 1.0, and truncating the
result to an integer. This, of course, is equivalent to sampling with
replacement from a finite population of size k.
occur with equal probability. A random integer is generated by
multiplying
k by a uniform (0,1) random number, adding 1.0, and truncating the
result to an integer. This, of course, is equivalent to sampling with
replacement from a finite population of size k.- Parameters:
k- Parameter of the discrete uniform distribution. The integers occur with equal probability.
Parameter k must be positive.
occur with equal probability.
Parameter k must be positive.- Returns:
- an
int, a pseudorandom number from a discrete uniform distribution. - See Also:
- Example
-
nextVonMises
public double nextVonMises(double c)
Generate a pseudorandom number from a von Mises distribution.Method
nextVonMisesgenerates pseudorandom numbers from a von Mises distribution with parameter c, which must be positive. With c = C, the probability density function is![fleft( x right) = frac{1}{{2pi I_0 left( c
right)}}exp left[ {c,cos left( x right)} right],for, - pi lt
x lt pi](eqn_2348.png)
where
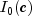 is the modified Bessel function of the
first kind of order 0. The probability density equals 0 outside the
interval
is the modified Bessel function of the
first kind of order 0. The probability density equals 0 outside the
interval
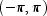 .
.The algorithm is an acceptance/rejection method using a wrapped Cauchy distribution as the majorizing distribution. It is due to Best and Fisher (1979).
- Parameters:
c- adoublewhich specifies the parameter of the von Mises distribution, .
.- Returns:
- a
double, a pseudorandom number from a von Mises distribution - See Also:
- Example
-
nextWeibull
public double nextWeibull(double a)
Generate a pseudorandom number from a Weibull distribution.Method
nextWeibullgenerates pseudorandom numbers from a Weibull distribution with shape parameter a. The probability density function is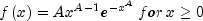
nextWeibulluses an antithetic inverse CDF technique to generate a Weibull variate; that is, a uniform random deviate U is generated and the inverse of the Weibull cumulative distribution function is evaluated at 1.0 - u to yield the Weibull deviate.Deviates from the two-parameter Weibull distribution, with shape parameter a and scale parameter b, can be generated by using
nextWeibulland then multiplying the result by b.The Rayleigh distribution with probability density function,
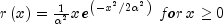
is the same as a Weibull distribution with shape parameter a equal to 2 and scale parameter b equal to
.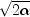
hence,
nextWeibulland simple multiplication can be used to generate Rayleigh deviates.- Parameters:
a- adoublewhich specifies the shape parameter of the Weibull distribution, a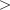 0
0- Returns:
- a
double, a pseudorandom number from a Weibull distribution - See Also:
- Example
-
nextZigguratNormalAR
public double nextZigguratNormalAR()
Generates pseudorandom numbers using the Ziggurat method.The
nextZigguratNormalARmethod cuts the density into many small pieces. For each random number generated, an interval is chosen at random and a random normal is generated from the choosen interval. In this implementation, the density is cut into 256 pieces, but symmetry is used so that only 128 pieces are needed by the computation. Following Doornik (2005), different uniform random deviates are used to determine which slice to use and to determine the normal deviate from the slice.- Returns:
- a
doublecontaining the random normal deviate.
-
setMultiplier
public void setMultiplier(int multiplier)
Sets the multiplier for a linear congruential random number generator. If a multiplier is set then the linear congruential generator, defined in the base classjava.util.Random, is replaced by the generator
seed = (multiplier*seed) mod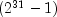
See Donald Knuth, The Art of Computer Programming, Volume 2, for guidelines in choosing a multiplier. Some possible values are 16807, 397204094, 950706376.- Parameters:
multiplier- anintwhich represents the random number generator multiplier
-
setSeed
public void setSeed(long seed)
Sets the seed.
-
skip
public void skip(int n)
Resets the seed to skip ahead in the base linear congruential generator. This method can be used only if a linear congruential multiplier is explicitly defined by a call tosetMultiplier. The method skips ahead in the deviates returned by the protected methodnext. The public methods usenext(int)as their source of uniform random deviates. Some methods call it more than once. For instance, each call tonextDoublecalls it twice.- Parameters:
n- is the number of random deviates to skip.
-
-