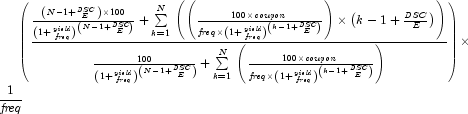Click or drag to resize
BondDuration Method
Returns the Macauley's duration of a security where the security has periodic interest payments.

Namespace: Imsl.Finance
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
Syntax
Copy
public static double Duration(
	DateTime settlement,
	DateTime maturity,
	double coupon,
	double yield,
	BondFrequency frequency,
	DayCountBasis basis
)

Parameters

settlement
Type: SystemDateTime
The DateTime settlement date of the security.
maturity
Type: SystemDateTime
The DateTime maturity date of the security.
coupon
Type: SystemDouble
A double which specifies the security's annual coupon rate.
yield
Type: SystemDouble
A double which specifies the security's annual yield.
frequency
Type: Imsl.FinanceBondFrequency
A int which specifies the number of coupon payments per year (1 for annual, 2 for semiannual, 4 for quarterly).
basis
Type: Imsl.FinanceDayCountBasis
A DayCountBasis object which contains the type of day count basis to use.

Return Value

Type: Double
A double which specifies the annual duration of a security with periodic interest payments.
Remarks

The Macauley's duration is the weighted-average time to the payments, where the weights are the present value of the payments. It is computed using the following:

\left({{{{{\left({N - 1 + {{\it DSC}\over E}}\right)\times 100}\over {\left({1 + {{\it yield}\over {\it freq} }}\right)^{\left({N - 1 + {{\it DSC}\over E}}\right)}}} + \sum \limits_{k = 1}^N {}\left({\left({{{100\times {\it coupon}}\over {{ \it freq}\times\left({1 + {{\it yield}\over {\it freq}}}\right)^{ \left({k - 1 + {{\it DSC}\over E}}\right)}}}}\right)\times\left({k - 1 + {{\it DSC}\over E}}\right)}\right)}\over{{{100} \over {\left( {1 + {{\it yield}\over {\it freq}}}\right)^{\left(N - 1 + {{\it DSC }\over E}\right)}}} + \sum\limits_{k = 1}^N {}\left({{{100 \times { \it coupon}}\over {{\it freq}\times\left({1 + {{\it yield}\over { \it freq}}}\right)^{\left(k - 1 + {{\it DSC}\over E}\right)}}}} \right)}}}\right)\times {1\over {\it freq}}
In the equation above, {\it DSC} represents the number of days starting with the settlement date and ending with the next coupon date. E represents the number of days within the coupon Frequency. N represents the number of coupons payable from the settlement date to the maturity date. {\it freq} represents the frequency of the coupon payments annually.

See Also