Cdf.Beta Method

Evaluates the beta cumulative probability distribution function.

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

public static double Beta(
	double x,
	double pin,
	double qin
)

Public Shared Function Beta ( 
	x As Double,
	pin As Double,
	qin As Double
) As Double

public:
static double Beta(
	double x, 
	double pin, 
	double qin
)

static member Beta : 
        x : float * 
        pin : float * 
        qin : float -> float

Parameters

x: Type: System.Double
A double, the argument at which the function is to be evaluated.
pin: Type: System.Double
A double, the first beta distribution parameter.
qin: Type: System.Double
A double, the second beta distribution parameter.

Return Value

Type: Double
A double, the probability that a beta random variable takes on a value less than or equal to x.

Remarks

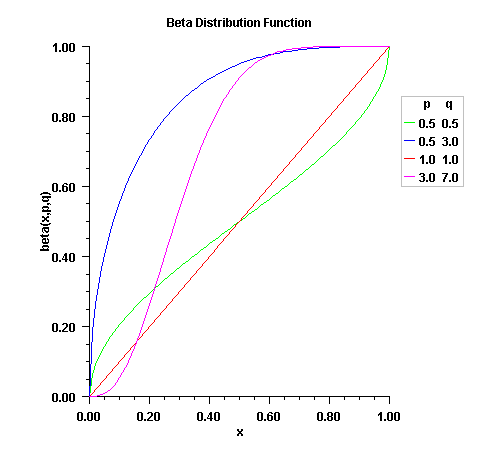
Method Cdf.Beta evaluates the distribution function of a beta random variable with parameters pin and qin. This function is sometimes called the incomplete beta ratio and, with p = pin and q = qin, is denoted by . It is given by

$I_x\left({p,\,q}\right)=\frac{{ \Gamma\left(p\right)\Gamma\left(q\right)}}{{\Gamma\left({p + q} \right)}}\int_0^x{\,t^{p-1}\left({1-t}\right)^{q-1}dt}$

where $\Gamma(\cdot)$ is the gamma function. The value of the distribution function is the probability that the random variable takes a value less than or equal to x.

The integral in the expression above is called the incomplete beta function and is denoted by $\beta_x(p, q)$ . The constant in the expression is the reciprocal of the beta function (the incomplete function evaluated at one) and is denoted by $\beta_1(p, q)$ .

Cdf.Beta uses the method of Bosten and Battiste (1974).

Plot of Beta Distribution Function

Reference

Cdf Class

Imsl.Stat Namespace

Other Resources

Example