| SignTest Class |
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The SignTest type exposes the following members.
| Name | Description | |
|---|---|---|
| Compute |
Performs a sign test.
| |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| NumPositiveDev |
Returns the number of positive differences. Note that the
Compute method must be invoked first before invoking this
method. Otherwise, the return value is 0.
| |
| NumZeroDev |
Returns the number of zero differences. Note that the Compute
method must be invoked first before invoking this method. Otherwise,
the return value is 0.
| |
| Percentage |
The percentage percentile of the population.
| |
| Percentile |
The hypothesized percentile of the population.
|
Class SignTest tests hypotheses about the proportion p of
a population that lies below a value q, where p and
q corresponds to the Percentage and Percentile
properties, respectively. In continuous distributions, this can be a
test that q is the 100 p-th percentile of the population
from which x was obtained. To carry out testing, SignTest
tallies the number of values above q in the number of positive
differences ![]() for
for
![]() . The binomial
probability of the number of values above q in the number of
positive differences
. The binomial
probability of the number of values above q in the number of
positive differences ![]() for
for
![]() or more values
above q is then computed using the proportion p and the
sample size in x (adjusted for the missing observations and
ties).
or more values
above q is then computed using the proportion p and the
sample size in x (adjusted for the missing observations and
ties).
Hypothesis testing is performed as follows for the usual null and alternative hypotheses:
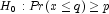 (the p-th
quantile is at least q)
(the p-th
quantile is at least q)
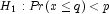
Reject
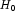 if probability is less than or
equal to the significance level.
if probability is less than or
equal to the significance level.
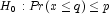 (the p-th
quantile is at least q)
(the p-th
quantile is at least q)
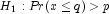
Reject
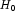 if probability is greater than
or equal to 1 minus the significance level.
if probability is greater than
or equal to 1 minus the significance level.
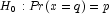 (the p-th quantile is
q)
(the p-th quantile is
q)
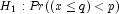 or
or
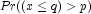
Reject
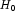 if probability is less than or
equal to half the significance level or greater than or equal to 1
minus half the significance level.
if probability is less than or
equal to half the significance level or greater than or equal to 1
minus half the significance level.
The assumptions are as follows:
- They are independent and identically distributed.
- Measurement scale is at least ordinal; i.e., an ordering less than, greater than, and equal to exists in the observations.
Many uses for the sign test are possible with various values of p
and q. For example, to perform a matched sample test that the
difference of the medians of y and z is 0.0, let
p = 0.5, q = 0.0, and ![]() in
matched observations y and z. To test that the median
difference is c, let q = c.
in
matched observations y and z. To test that the median
difference is c, let q = c.