Sort Class

Sort Class

A collection of sorting functions.

Inheritance Hierarchy

SystemObject
Imsl.StatSort

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

C++

Copy

[SerializableAttribute]
public class Sort

<SerializableAttribute>
Public Class Sort

[SerializableAttribute]
public ref class Sort

[<SerializableAttribute>]
type Sort =  class end

The Sort type exposes the following members.

Methods

	Name	Description
	Ascending(Double)	Sort an array into ascending order.
	Ascending(Int32)	Function to sort an integer array into ascending order.
	Ascending(Double, Int32)	Sort a matrix into ascending order by the first nKeys.
	Ascending(Double, Int32)	Sort a matrix into ascending order by specified keys.
	Ascending(Double, Int32)	Sort an array into ascending order and returns the permutation vector.
	Ascending(Int32, Int32)	Sort an integer array into ascending order and returns the permutation vector.
	Ascending(Double, Int32, Int32)	Sort an array into ascending order by the first nKeys and returns the permutation vector.
	Ascending(Double, Int32, Int32)	Sort a matrix into ascending order by specified keys and returns the permutation vector.
	Descending(Double)	Sort an array into descending order.
	Descending(Int32)	Function to sort an integer array into descending order.
	Descending(Double, Int32)	Function to sort a matrix into descending order by the first nKeys.
	Descending(Double, Int32)	Function to sort a matrix into descending order by specified keys.
	Descending(Double, Int32)	Sort an array into descending order and returns the permutation vector.
	Descending(Int32, Int32)	Sort an integer array into descending order and returns the permutation vector.
	Descending(Double, Int32, Int32)	Function to sort an array into descending order by the first nKeys and returns the permutation vector.
	Descending(Double, Int32, Int32)	Function to sort a matrix into descending order by specified keys and return the permutation vector.
	Equals	Determines whether the specified object is equal to the current object. (Inherited from Object.)
	Finalize	Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.)
	GetHashCode	Serves as a hash function for a particular type. (Inherited from Object.)
	GetType	Gets the Type of the current instance. (Inherited from Object.)
	MemberwiseClone	Creates a shallow copy of the current Object. (Inherited from Object.)
	ToString	Returns a string that represents the current object. (Inherited from Object.)

Top

Remarks

Class Sort contains ascending and descending methods for sorting elements of an array or a matrix.

The QuickSort algorithm is used, except for short sequences which are handled using an insertion sort.

The QuickSort algorithm is a randomized QuickSort with 3-way partitioning. Basic QuickSort is slow if the sequence to be sorted contains many duplicate keys. The 3-way partitioning algorithm elimiates this problem. The pivot is chosen as the middle element of three potential pivots chosen at random.

The matrix ascending method sorts the rows of real matrix x using a particular row in x as the keys. The sort is algebraic with the first key as the most significant, the second key as the next most significant, etc. When x is sorted in ascending order, the resulting sorted array is such that the following is true:

For $i = 0, 1, \ldots, {\rm n\_observations} - 2, {\rm x} [i] [{\rm indices\_keys} \,\,[0]] \leq {\rm x}[i + 1] [{\rm indices\_keys} [0]]$
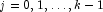For $k = 1, \ldots, {\rm n\_keys - 1, if\,\, x [i] [{\rm indices\_keys} [j]] = x [i + 1] [{\rm indices\_keys} [j]]}$ for $j = 0, 1, \ldots, k - 1$ , then ${\rm x} [i] [{\rm indices\_keys} [k]] = {\rm x} [i + 1] [{\rm indices\_keys} [k]]$

The observations also can be sorted in descending order. The rows of x containing the missing value code NaN in at least one of the specified columns are considered as an additional group. These rows are moved to the end of the sorted x.

If all of the sort keys in a pair of rows are equal then the rows keep their original relative order.

The sorting algorithm is based on a quicksort method given by Singleton (1969) with modifications, see Bentley and Sedgewick (1997).

Reference

Imsl.Stat Namespace

Other Resources

Example 1: Array sort with permutation vector

Example 2: Matrix sort containing NaN's