mlffInitializeWeights¶
Initializes weights for multilayered feedforward neural networks prior to network training using one of four user selected methods.
Synopsis¶
mlffInitializeWeights (network, nominal, continuous)
Required Arguments¶
- Imsls_d_NN_Network
network(Input/Output) - A Imsls_d_NN_Network containing the parameters that define the
feedforward network’s architecture, including network weights and bias
values. For more details, see mlffNetwork. When
network training is successful, the weights and bias values in
networkare replaced with the values calculated for the optimum trained network. - int
nominal[[]](Input) - Array of size
nPatternsbynNominalcontaining the nominal input variables. - float
continuous[[]](Input) - Array of size
nPatternsbynContinuouscontaining the continuous and scaled ordinal input variables.
Return Value¶
An array of length network.n_links +
(network.n_nodes-network.nInputs) containing the initialized
weights. See the Description section for
details on weight ordering.
Optional Arguments¶
method, int (Input)Specifies the algorithm to use for initializing weights.
methodcontains the weight initialization method to be used. Valid values formethodare:methodAlgorithm EQUALEqual weights RANDOMRandom Weights PRINCIPAL_COMPONENTSPrincipal Component Weights DISCRIMINANTDiscriminant Analysis Weights The discriminant weights method can only be used to initialize weights for classification networks without binary encoded nominal attributes. See the Description section for details.
Default:
method=RANDOM.t_print, (Input)Initial weights are printed.
Default: No printing is performed.
classification, int[](Input)- An array of length nPatterns containing the encoded training target
classifications which must be integers from 0 to
nClasses-1. HerenClasses=network.n_outputsexcept whennOutputs=1 thennClasses=2.classification[i]is the target classification for the i-th training pattern described bynominal[i]andcontinuous[i]. This option is used by the discriminant analysis weight initialization. This option is ignored for all other methods.
Description¶
Function mlffInitializeWeights calculates initial values for the weights
of a feedforward neural network using one of the following algorithms:
method |
Algorithm |
|---|---|
EQUAL |
Equal weights |
RANDOM |
Random Weights |
PRINCIPAL_COMPONENTS |
Principal Component Weights |
DISCRIMINANT |
Discriminant Analysis Weights |
The keyword method can be used to select the algorithm for weight
initialization. By default, the random weights algorithm will be used.
The 3-layer feed forward network with 3 input attributes and 6 perceptrons in Figure 13.12 is used to describe the initialization algorithms. In this example, one of the input attributes is continuous (\(X_3\)) and the others are nominal (\(X_1\) and \(X_2\)).
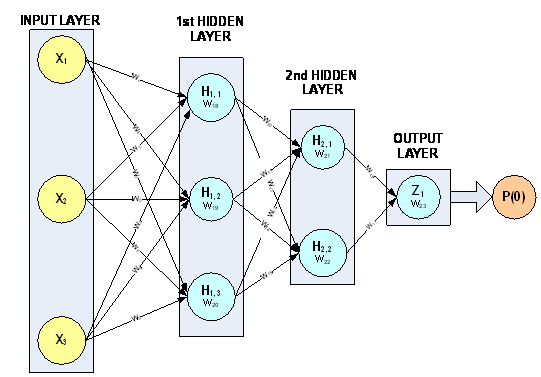
Figure 13.12 — A 3-layer, Feed Forward Network with 3 Input Attributes and 6 Perceptrons
This network has a total of 23 weights. The first nine weights, labeled \(W_1,W_2,\ldots,W_9\), are the weights assigned to the links connecting the network inputs to the perceptrons in the first hidden layer. Note that \(W_1\), \(W_2\), \(W_4\), \(W_5\), \(W_7\), and \(W_8\) are assigned to the two nominal attributes and \(W_3\), \(W_6\) and \(W_9\) are assigned to the continuous attribute. All neural network functions in the C Stat Library use this weight ordering. Weights for all nominal attributes are placed before the weights for any continuous attributes.
PERCEPTRON |
POTENTIAL |
|---|---|
| \(\text{H}_{1,1}\) | \(g_1=W_{18}+W_1 X_1+W_2 X_2+W_3 X_3\) |
| \(\text{H}_{1,2}\) | \(g_2=W_{19}+W_4 X_1+W_5 X_2+W_6 X_3\) |
| \(\text{H}_{1,3}\) | \(g_3=W_{20}+W_7 X_1+W_8 X_2+W_9 X_3\) |
| \(\text{H}_{2,1}\) | \(g_4=W_{21}+W_{10} g_1+W_{11} g_2+W_{12} g_3\) |
| \(\text{H}_{2,2}\) | \(g_5=W_{22}+W_{13} g_1+W_{14} g_2+W_{15} g_3\) |
| \(\text{Z}_1\) | \(g_6=W_{23}+W_{16} g_4+W_{17} g_5\) |
The next six weights are the weights between the first and second hidden
layers, and \(W_{16}\) and \(W_{17}\) are the weights for the links
connecting the second hidden layer to the output layer. The last six elements
in the weights array are the perceptron bias weights. These weights,
\(W_{18},W_{19},\ldots,W_{23}\) are the weights for perceptrons
\(H_{1,1,\ldots}\), \(H_{1,3}\), \(H_{2,1,\ldots}\),
\(H_{2,3}\), and \(Z_1\), respectively.
The perceptron potential calculations for this network are described in the table above. Following the notation presented in the introduction to this chapter, \(g_1,g_2,\cdots,g_5\) are the perceptron activations from perceptrons \(H_{1,1,\ldots}\), \(H_{1,3}\), \(H_{2,1\ldots}\), \(H_{2,3}\), respectively.
All initialization algorithms in mlffInitializeWeights set the weights
for perceptrons not linked directly to the input perceptrons in the same
manner. Bias weights for perceptrons not directly linked to input attributes
are set to zero. All non-bias weights for these same perceptrons are
assigned a value of \(1/k\) where k=the number of links into that
perceptron (network.nodes[i].n_inlinks).
For example, in this network, the last three bias weights \(W_{21}\), \(W_{22}\) and \(W_{23}\) are initialized to zero since perceptrons \(H_{2,1,}\) \(H_{2,1}\) and \(Z_1\) and not directly connected to the input attributes. The other weights to perceptrons \(H_{2,1}\) and \(H_{2,2}\) are assigned a value of one half since these perceptrons each have only two input links. The weights to the output perceptron, \(Z_1\), are also one half since \(Z_1\) has two inputs links.
The calculation of the weights for the links between the input attributes and their perceptrons are initialized differently by the four algorithms. All algorithms, however, scale these weights so that the average potential for the first layer perceptrons is zero. This reduces the possibility of saturation or numerical overflow during the initial stages of optimization.
Equal Weights (method=EQUAL)
In this algorithm, the non-bias weights for each link between the input attributes and the perceptrons in the first layer are initialized to:
where \(W_i\) is the weight for all links between the i-th input attributes, n is equal to the total number of input attributes and \(S_i\) is equal to the standard deviation of the potential for the i-th input attribute. In the above example, the values for weights \(W_1,W_2,\ldots,W_9\), each would be set to:
since this network has three input attributes.
Next the average potential for each of the perceptrons connected to the input layer is calculated by:
where \(\overline{X}_i\) is equal to the average potential for the i-th input attribute. All other bias weights are set to zero.
Random Weights (method=RANDOM)
This algorithm first generates random values for the input layer weights using the Uniform [-0.5, +0.5] distribution. These are then scaled using the standard deviation of the input layer potentials.
where U is a random number uniformly distributed on the interval [-0.5,+0.5] and \(S_i\) is equal to the standard deviation of the potential for the i-th input attribute.
Next the average potential for each of the perceptrons connected to the input layer is calculated by:
where \(\overline{X}_i\) is equal to the average potential for the i-th input attribute. All other bias weights are set to zero.
Principal Component Weights (method=PRINCIPAL_COMPONENTS)
This uses principal component analysis to generate weights. The arrays nominal and continuous are combined into a single matrix. The correlation matrix of this matrix is decomposed using principal component analysis. The elements of the principal components from this analysis are used to initialize weights associated with the network inputs. As with the other methods the principal component weights are scaled by using the standard deviation of the potential for the perceptrons connected to the input layer:
where \(W_i\) is the weight for the link between the i-th input attribute and the j-th perceptron, \(\xi_{ij}\) is the i-th value of the j-th principal component, and \(S_i\) is equal to the standard deviation of the potential for the i-th input attribute.
If the number of principal components is less than the number of perceptrons
in the first layer, i.e., (nContinuous+nNominal) < n_layer1,
where n_layer1 is the number of perceptrons in the first layer, then it is
not possible to initialize all weights with principal components. In this
case, the first (nContinuous + nNominal) perceptrons are initialized
using the principal components and then the remainder are initialized using
random weights (method=RANDOM).
As with the other methods, the bias weights for each of the first layer perceptrons is set to ensure that the average potential in this layer is equal to zero:
where \(\overline{X}_{ij}\) is equal to the average potential for the link between i-th input attribute and the j-th first layer perceptron, and \(S_{ij}\) is the standard deviation for this same potential.
Discriminant Weights (method=DISCRIMINANT)
This method is very similar to principal component weights. Instead the discriminant analysis elements replace the principal component elements. The weights between the i-th input attribute and the j-th perceptron in the first layer are calculated by:
Where \(W_i\) is the weight for the link between the i-th input attribute and the j-th perceptron, \(\theta_{ij}\) is the i-th value of the j-th discriminant component, and \(S_i\) is equal to the standard deviation of the potential for the i-th input attribute.
If the number of discriminant components is less than the number of
perceptrons in the first layer, i.e., (nContinuous + nNominal) <
n_layer1, where n_layer1 is the number of perceptrons in the first
layer, then it is not possible to initialize all weights with components
from the discriminant analysis. In this case, the first (nContinuous +
nNominal) perceptrons are initialized using the discriminant components
and then the remainder are initialized using random weights
(method=RANDOM).
As with the other methods, the bias weights for each of the first layer perceptrons is set to ensure that the average potential in this layer is equal to zero:
where \(\overline{X}_{ij}\) is equal to the average potential for the link between i-th input attribute and the j-th first layer perceptron, and \(S_{ij}\) is the standard deviation for this same potential.
Examples¶
Example 1¶
This example illustrates random initialization algorithms for a three layer network with one output. The first and second hidden layers contain three and two perceptrons for a total of five network perceptrons, respectively.
The nine input attributes consist of two continuous attributes plus seven binary attributes encoded from two nominal attributes using binary encoding.
The weights are initialized using the random weights algorithm. This results in different weights for every perceptron in the first hidden layer. The weights in other layers are initialized using equal weights. It should be noted that the bias weights in the first layer are not random. Except for the discriminant weights algorithm, the bias weights are always calculated to ensure that the average potential for each perceptron in the first layer is zero.
from __future__ import print_function
from numpy import empty, int
from pyimsl.stat.mlffInitializeWeights import mlffInitializeWeights
from pyimsl.stat.mlffNetwork import mlffNetwork
from pyimsl.stat.mlffNetworkInit import mlffNetworkInit
from pyimsl.stat.randomSeedSet import randomSeedSet
from pyimsl.stat.unsupervisedNominalFilter import unsupervisedNominalFilter
n_patterns = 24 # no. of training patterns
n_nvars = 2 # 2 nominal unencoded variables
n_nominal = 7 # 7 inputs for the binary encoded nominal vars
n_continuous = 2 # 2 continuous input attributes
nominalIn = empty([24], dtype=int) # work array used to encode nominal data
classification = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1]
# raw nominal input data
nominal_unencododed = [[0, 0], [0, 1], [0, 2],
[1, 0], [1, 1], [1, 2],
[2, 0], [2, 1], [2, 2],
[3, 0], [3, 1], [3, 2],
[0, 0], [0, 1], [0, 2],
[1, 0], [1, 1], [1, 2],
[2, 0], [2, 1], [2, 2],
[3, 0], [3, 1], [3, 2]]
# input array for binary encoded version of
# nominal_unencododed[] array above
nominal = empty([24, 7], dtype=int)
continuous = [[0.00, 0.00], [0.02, 0.02], [0.04, 0.04], [0.06, 0.06],
[0.08, 0.08], [0.10, 0.10], [0.12, 0.12], [0.14, 0.14],
[0.16, 0.16], [0.18, 0.18], [0.20, 0.20], [0.22, 0.22],
[0.24, 0.28], [0.26, 0.30], [0.28, 0.32], [0.30, 0.34],
[0.32, 0.36], [0.34, 0.38], [0.36, 0.40], [0.38, 0.42],
[0.40, 0.44], [0.42, 0.46], [0.44, 0.48], [0.46, 0.50]]
# Setup Nominal Input Attributes Using Binary Encoding */
m = 0
for i in range(0, n_nvars):
for j in range(0, n_patterns):
nominalIn[j] = nominal_unencododed[j][i] + 1
n_classes = []
nominalOut = unsupervisedNominalFilter(n_classes, nominalIn)
for k in range(0, n_classes[0]):
for j in range(0, n_patterns):
nominal[j, m] = nominalOut[j, k]
m = m + 1
# nominal[j,k] = nominalOut[j,k]
print("\tINPUT TRAINING PATTERNS")
print("\tY Nom1 Nom2 X0 X1 ")
for i in range(0, n_patterns):
print("\t%d %d \t %d %f %f " %
(classification[i],
nominal_unencododed[i][0],
nominal_unencododed[i][1],
continuous[i][0], continuous[i][1]))
# Binary classification network 9 inputs 1 output = 2 classes
network = mlffNetworkInit(9, 1)
mlffNetwork(network, createHiddenLayer=3)
mlffNetwork(network, createHiddenLayer=2, linkAll=True)
# Note the following statement is for repeatable output
randomSeedSet(5555)
# Random Weights
weights = mlffInitializeWeights(network, nominal, continuous, t_print=True)
Output¶
INPUT TRAINING PATTERNS
Y Nom1 Nom2 X0 X1
0 0 0 0.000000 0.000000
0 0 1 0.020000 0.020000
0 0 2 0.040000 0.040000
0 1 0 0.060000 0.060000
0 1 1 0.080000 0.080000
0 1 2 0.100000 0.100000
1 2 0 0.120000 0.120000
1 2 1 0.140000 0.140000
1 2 2 0.160000 0.160000
1 3 0 0.180000 0.180000
1 3 1 0.200000 0.200000
1 3 2 0.220000 0.220000
0 0 0 0.240000 0.280000
0 0 1 0.260000 0.300000
0 0 2 0.280000 0.320000
0 1 0 0.300000 0.340000
0 1 1 0.320000 0.360000
0 1 2 0.340000 0.380000
1 2 0 0.360000 0.400000
1 2 1 0.380000 0.420000
1 2 2 0.400000 0.440000
1 3 0 0.420000 0.460000
1 3 1 0.440000 0.480000
1 3 2 0.460000 0.500000
-------------------------------------------
- NETWORK WEIGHTS INITIALIZED USING
- RANDOM WEIGHTS
- Input Attributes: 9
- Nominal: 2
- Nominal(encoded): 7
- Continuous: 2
- Output Attributes: 1
- n_classes: 2
- Layers: 3
- Perceptrons: 6
- Weights: 41
- Patterns: 24
-------------------------------------------
------------- HIDDEN LAYER 1 -------------
--- Perceptron 0 ---
Link from Input Node Weight
N0 0.937067
N1 -0.547568
N2 1.468245
N3 0.107160
N4 -0.884990
N5 -0.814067
N6 -1.979676
X7 -0.041228
X8 -1.368312
Bias 3.30989
--- Perceptron 1 ---
Link from Input Node Weight
N0 -0.308421
N1 -1.058449
N2 -0.981207
N3 1.040820
N4 -0.033492
N5 -0.575732
N6 0.571939
X7 0.811886
X8 -0.415498
Bias 0.573286
--- Perceptron 2 ---
Link from Input Node Weight
N0 -1.117744
N1 0.620799
N2 0.174895
N3 -0.100458
N4 -0.961071
N5 0.854179
N6 0.046424
X7 0.880998
X8 -0.903982
Bias 1.00437
-------------------------------------------
------------- HIDDEN LAYER 2 -------------
--- Perceptron 0 ---
Link from Input Node Weight
P0 0.333333
P1 0.333333
P2 0.333333
Bias 0
--- Perceptron 1 ---
Link from Input Node Weight
P0 0.333333
P1 0.333333
P2 0.333333
Bias 0
-------------------------------------------
------------- OUTPUT LAYER -------------
--- Perceptron 0 ---
Link from Input Node Weight
P3 0.500000
P4 0.500000
Bias 0
-------------------------------------------
Example 2¶
This example illustrates the discriminant weights initialization algorithm for a three layer network with one output. The first and second hidden layers contain three and two perceptrons for a total of five network perceptrons, respectively.
The data are the same as Example 1, and the network structure is the same except that all nominal input attributes are removed. This was necessary since the discriminant weights algorithm only works when all input attributes are continuous.
The discriminant weights algorithm initializes the weights in the first hidden layer to the coefficients of the discriminant functions. Since this example is a binary classification example, the number of discriminant functions is equal to the number of classes, two, but there are three perceptrons in the first layer. The weights for the first two perceptrons in this layer are the discriminant function coefficients, including the bias weight. The weights for the last perceptron in this layer were determined randomly.
from __future__ import print_function
from pyimsl.stat.mlffInitializeWeights import mlffInitializeWeights, DISCRIMINANT
from pyimsl.stat.mlffNetwork import mlffNetwork
from pyimsl.stat.mlffNetworkInit import mlffNetworkInit
from pyimsl.stat.randomSeedSet import randomSeedSet
n_patterns = 24 # no. of training patterns
n_continuous = 2 # 2 continuous input attributes
classification = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1]
continuous = [[0.00, 0.00], [0.02, 0.02], [0.04, 0.04], [0.06, 0.06],
[0.08, 0.08], [0.10, 0.10], [0.12, 0.12], [0.14, 0.14],
[0.16, 0.16], [0.18, 0.18], [0.20, 0.20], [0.22, 0.22],
[0.24, 0.28], [0.26, 0.30], [0.28, 0.32], [0.30, 0.34],
[0.32, 0.36], [0.34, 0.38], [0.36, 0.40], [0.38, 0.42],
[0.40, 0.44], [0.42, 0.46], [0.44, 0.48], [0.46, 0.50]]
print("\tINPUT TRAINING PATTERNS")
print("\tY X0 X1 ")
for i in range(0, n_patterns):
print("\t%d %f %f " %
(classification[i],
continuous[i][0], continuous[i][1]))
# Binary classification network 2 inputs 1 output = 2 classes
network = mlffNetworkInit(2, 1)
mlffNetwork(network, createHiddenLayer=3)
mlffNetwork(network, createHiddenLayer=2, linkAll=True)
# Discriminant weights
# Set seed for consistent results
randomSeedSet(12357)
weights = mlffInitializeWeights(network, None, continuous,
method=DISCRIMINANT,
classification=classification,
t_print=True)
Output¶
INPUT TRAINING PATTERNS
Y X0 X1
0 0.000000 0.000000
0 0.020000 0.020000
0 0.040000 0.040000
0 0.060000 0.060000
0 0.080000 0.080000
0 0.100000 0.100000
1 0.120000 0.120000
1 0.140000 0.140000
1 0.160000 0.160000
1 0.180000 0.180000
1 0.200000 0.200000
1 0.220000 0.220000
0 0.240000 0.280000
0 0.260000 0.300000
0 0.280000 0.320000
0 0.300000 0.340000
0 0.320000 0.360000
0 0.340000 0.380000
1 0.360000 0.400000
1 0.380000 0.420000
1 0.400000 0.440000
1 0.420000 0.460000
1 0.440000 0.480000
1 0.460000 0.500000
Discriminant Analysis Classification Error Rate = 0.000000
-------------------------------------------
- NETWORK WEIGHTS INITIALIZED USING
- DISCRIMINANT WEIGHTS
- Input Attributes: 2
- Nominal: 0
- Nominal(encoded): 0
- Continuous: 2
- Output Attributes: 1
- n_classes: 2
- Layers: 3
- Perceptrons: 6
- Weights: 20
- Patterns: 24
-------------------------------------------
------------- HIDDEN LAYER 1 -------------
--- Perceptron 0 ---
Link from Input Node Weight
X0 229.166667
X1 -189.880952
Bias -2.13362
--- Perceptron 1 ---
Link from Input Node Weight
X0 889.166667
X1 -755.595238
Bias -12.5051
--- Perceptron 2 ---
Link from Input Node Weight
X0 -4.495920
X1 -0.976039
Bias 6.07221
-------------------------------------------
------------- HIDDEN LAYER 2 -------------
--- Perceptron 0 ---
Link from Input Node Weight
P0 0.333333
P1 0.333333
P2 0.333333
Bias 0
--- Perceptron 1 ---
Link from Input Node Weight
P0 0.333333
P1 0.333333
P2 0.333333
Bias 0
-------------------------------------------
------------- OUTPUT LAYER -------------
--- Perceptron 0 ---
Link from Input Node Weight
P3 0.500000
P4 0.500000
Bias 0
-------------------------------------------