mlffNetworkTrainer¶

Trains a multilayered feedforward neural network.

Synopsis¶

mlffNetworkTrainer (network, nominal, continuous, output)

Required Arguments¶

Imsls_d_NN_Network network (Input/Output)

A Imsls_d_NN_Network containing the feedforward network. See mlffNetwork. On return, the weights and bias values are updated.

int nominal[[]] (Input)

Array of size nPatterns by nNominal containing values for the nominal input attributes. The i-th row contains the nominal input attributes for the i-th training pattern.

float continuous[[]] (Input)

Array of size nPatterns by nContinuous containing values for the continuous input attributes. The i-th row contains the continuous input attributes for the i-th training pattern.

float output[[]] (Input)

Array of size nPatterns by nOutputs containing the output training patterns, where nOutputs is the number of output perceptrons in the network.

nOutputs = network.n_outputs. For more details, see mlffNetwork.

Return Value¶

An array of length 5 containing the summary statistics from the network training, organized as follows:

Element	Training Statistics
0	Error sum of squares at the optimum.
1	Total number of Stage I iterations.
2	Smallest error sum of squares after Stage I training.
3	Total number of Stage II iterations.
4	Smallest error sum of squares after Stage II training.

If training is unsuccessful, None is returned.

Optional Arguments¶

stageI, int nEpochs, int epochSize (Input)

Argument nEpochs is the number epochs used for Stage I training and argument epochSize is the number of patterns used during each epoch. If epoch training is not needed, set epochSize = nPatterns and nEpochs = 1. Stage I is implemented using Quasi-Newton optimization and steepest ascent with gradients estimated using the backward propagation method.

Default: nEpochs=15, epochSize = nPatterns.

noStageII, (Input)

Specifies no Stage II training is performed. Stage II is implemented using Quasi-Newton optimization with numerical gradients.

Default: Stage II training is performed.

maxStep, float (Input)

Maximum allowable step size in the optimizer.

Default: maxStep = 1000.

maxItn, int (Input)

Maximum number of iterations in the optimizer, per epoch.

Default: maxItn = 1000.

maxFcn, int (Input)

Maximum number of function evaluations in the optimizer, per epoch.

Default: maxFcn = 400.

relFcnTol, float (Input)

Relative function tolerance in the optimizer.

Default: relFcnTol = \(\max(10^{-10},\varepsilon^{2/3})\), where ɛ is the machine precision.

gradTol, float (Input)

Scaled gradient tolerance in the optimizer.

Default: gradTol = \(\varepsilon^{1/2}\), where ɛ is the machine precision.

tolerance, float (Input)

Absolute accuracy tolerance for the sum of squared errors in the optimizer.

Default: tolerance = 0.1.

weightInitializationMethod, int[] (Input)

The method to use for initializing network weights prior to network training. One of the following four values is accepted:

`weightInitializationMethod`	Algorithm
`EQUAL`	Equal weights.
`RANDOM`	Random weights.
`PRINCIPAL_COMPONENTS`	Principal Component Weights.
`NN_NETWORK`	No initialization method will be performed. Weights in `NN_Network` structure `network` will be used instead.

See mlffInitializeWeights for a detailed description of the initialization methods.

Default: method = RANDOM.

t_print, (Input)

Intermediate results are printed during network training.

Default: No printing is performed.

residual (Output)

Array of size nPatterns by nOutputs containing the residuals for each observation in the training data, where nOutputs is the number of output perceptrons in the network.

nOutputs = network.n_outputs.

gradient (Output)

The array of size nLinks + n_nodes-nInputs to store the gradients for each weight found at the optimum training stage, where nLinks = network.n_links, nNodes = network.n_nodes, and

nInputs = network.n_inputs.

forecasts (Output)

The array of size nPatterns by nOutputs, where nOutputs is the number of output perceptrons in the network. nOutputs = network.n_outputs. The values of the i-th row are the forecasts for the outputs for the i-th training pattern.

Description¶

Function mlffNetworkTrainer trains a multilayered feedforward neural network returning the forecasts for the training data, their residuals, the optimum weights and the gradients associated with those weights. Linkages among perceptrons allow for skipped layers, including linkages between inputs and perceptrons. The linkages and activation function for each perceptron, including output perceptrons, can be individually configured. For more details, see optional arguments linkAll, linkLayer, and linkNode in mlffNetwork.

Training Data¶

Neural network training patterns consist of the following three types of data:

nominal input attributes
continuous input attributes
continuous output

The first data type contains the encoding of any nominal input attributes. If binary encoding is used, this encoding consists of creating columns of zeros and ones for each class value associated with every nominal attribute. If only one attribute is used for input, then the number of columns is equal to the number of classes for that attribute. If more columns appear in the data, then each nominal attribute is associated with several columns, one for each of its classes.

Each column consists of zeros, if that classification is not associated with this case, otherwise, one if that classification is associated. Consider an example with one nominal variable and two classes: male and female (male, male, female, male, female). With binary encoding, the following matrix is sent to the training engine to represent this data:

\[\begin{split}\mathit{nominalAtt} = \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\end{split}\]

Continuous input and output data are passed to the training engine using the arrays: continuous and output. The number of rows in each of these matrices is nPatterns. The number of columns in continuous and output, corresponds to the number of input and output variables, respectively.

Network Configuration¶

The network configuration consists of the following:

the number of inputs and outputs,
the number of hidden layers,
a description of the number of perceptrons in each layer,
and a description of the linkages among the perceptrons.

This description is passed into mlffNetworkTrainer using the structure Imsls_d_NN_Network. See mlffNetwork.

Training Efficiency¶

The training efficiency determines the time it takes to train the network. This is controlled by several factors. One of the most important factors is the initial weights used by the optimization algorithm. These are taken from the initial values provided in the structure Imsls_d_NN_Network, network.links[i].weight. Equally important are the scaling and filtering applied to the training data.

In most cases, all variables, particularly output variables, should be scaled to fall within a narrow range, such as [0, 1]. If variables are unscaled and have widely varied ranges, then numerical overflow conditions can terminate network training before an optimum solution is calculated.

Output¶

Output from mlffNetworkTrainer consists of scaled values for the network outputs, a corresponding forecast array for these outputs, a weights array for the trained network, and the training statistics. The Imsls_d_NN_Network structure is updated with the weights and bias values and can be used as input to mlffNetworkForecast.

The trained network can be saved and retrieved using mlffNetworkWrite and mlffNetworkRead.

Example¶

This example trains a two-layer network using 100 training patterns from one nominal and one continuous input attribute. The nominal attribute has three classifications which are encoded using binary encoding. This results in three binary network input columns. The continuous input attribute is scaled to fall in the interval [0,1].

The network training targets were generated using the relationship:

\[Y = 10X_1 + 20X_2 + 30X_3 + 20X_4,\]

where \(X_1\), \(X_2\), \(X_3\) are the three binary columns, corresponding to the categories 1‑3 of the nominal attribute, and \(X_4\) is the scaled continuous attribute.

The structure of the network consists of four input nodes and two layers, with three perceptrons in the hidden layer and one in the output layer. The following figure illustrates this structure:

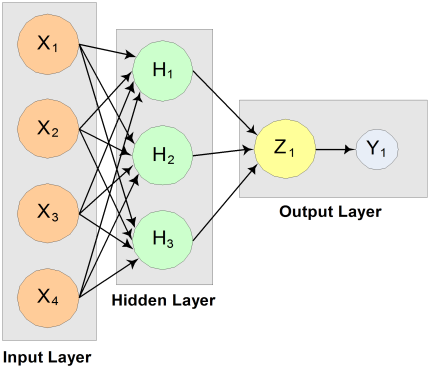
Figure 13.13 — A 2-layer, Feedforward Network with 4 Inputs and 1 Output

There are a total of 15 weights and 4 bias weights in this network. The activation functions are all linear.

Since the target output is a linear function of the input attributes, linear activation functions guarantee that the network forecasts will exactly match their targets. Of course, the same result could have been obtained using multiple regression. Printing is turned on to show progress during the training session.

from __future__ import print_function
from numpy import *
from readMlffNetworkData import readMlffNetworkData
from pyimsl.stat.mlffNetwork import mlffNetwork, LINEAR
from pyimsl.stat.mlffNetworkFree import mlffNetworkFree
from pyimsl.stat.mlffNetworkInit import mlffNetworkInit
from pyimsl.stat.mlffNetworkTrainer import mlffNetworkTrainer
from pyimsl.stat.randomSeedSet import randomSeedSet

# A 2D matrix of values for the nominal training
# attribute.  In this example, the single nominal
# attribute has 3 categories that are encoded using binary
# encoding for input into the network.
#
# [1,0,0] = category 1
# [0,1,0] = category 2
# [0,0,1] = category 3

nominal, continuous, output = readMlffNetworkData()

# A 2D matrix containing the training outputs for this network.
# In this case there is an exact linear relationship between these
# outputs and the inputs: output = 10*X1 +20*X2 + 30*X3 +2*X4,
# where X1-X3 are the nominal variables and X4 is the continuous
# attribute variable.   Output is unscaled.

hidActFcn = [LINEAR, LINEAR, LINEAR]

# Scale continuous attribute into the interval [0,1]
# and generate outputs
output = empty(100)
for i in range(0, 100):
    continuous[i] = continuous[i] / 10.0
    output[i] = (10 * nominal[i, 0]) + \
        (20 * nominal[i, 1]) + \
        (30 * nominal[i, 2]) + \
        (20 * continuous[i])

network = mlffNetworkInit(4, 1)

mlffNetwork(network, createHiddenLayer=3,
            activationFcn={'layerId': 1, 'activationFcn': hidActFcn},
            linkAll=True)

for i in range(0, network[0].n_links):
    # Hidden layer 1
    if (network[0].nodes[network[0].links[i].to_node].layer_id == 1):
        network[0].links[i].weight = .25

    # Output layer
    if (network[0].nodes[network[0].links[i].to_node].layer_id == 2):
        network[0].links[i].weight = .25

# Initialize seed for consistent results
randomSeedSet(12345)
forecasts = []
residual = []
stats = mlffNetworkTrainer(network, nominal, continuous, output,
                           stageI={'nEpochs': 10, 'epochSize': 100}, maxFcn=1000, relFcnTol=1.0e-20,
                           gradTol=1.0e-20, maxStep=5.0, tolerance=1.0e-5, t_print=True,
                           residual=residual, forecasts=forecasts)

print("Predictions for last 10 observations: ")
for i in range(90, 100):
    print("observation[%2i] %10.6f Prediction %10.6f Residual %10.6f"
          % (i, output[i], forecasts[i][0], residual[i][0]))

# Hidden layer nodes bias value * link weight
bias = network[0].nodes[network[0].n_nodes - 4].bias * \
    network[0].links[12].weight + \
    network[0].nodes[network[0].n_nodes - 3].bias * \
    network[0].links[13].weight + \
    network[0].nodes[network[0].n_nodes - 2].bias * \
    network[0].links[14].weight

bias += network[0].nodes[network[0].n_nodes - 1].bias  # output node
coef1 = network[0].links[0].weight * network[0].links[12].weight
coef1 += network[0].links[4].weight * network[0].links[13].weight
coef1 += network[0].links[8].weight * network[0].links[14].weight
coef2 = network[0].links[1].weight * network[0].links[12].weight
coef2 += network[0].links[5].weight * network[0].links[13].weight
coef2 += network[0].links[9].weight * network[0].links[14].weight
coef3 = network[0].links[2].weight * network[0].links[12].weight
coef3 += network[0].links[6].weight * network[0].links[13].weight
coef3 += network[0].links[10].weight * network[0].links[14].weight
coef4 = network[0].links[3].weight * network[0].links[12].weight
coef4 += network[0].links[7].weight * network[0].links[13].weight
coef4 += network[0].links[11].weight * network[0].links[14].weight
coef1 += bias
coef2 += bias
coef3 += bias

print("Bias: ", bias)
print("X1: %10.6f" % coef1)
print("X2: %10.6f" % coef2)
print("X3: %10.6f" % coef3)
print("X4: %10.6f" % coef4)

mlffNetworkFree(network)

Output¶

TRAINING PARAMETERS:
Stage II Opt.   = 1
n_epochs        = 10
epoch_size      = 100
max_itn         = 1000
max_fcn         = 1000
max_step        = 5.000000
rfcn_tol        = 1e-20
grad_tol        = 1e-20
tolerance       = 0.000010

STAGE I TRAINING STARTING
Stage I: Epoch 1 - Epoch Error SS = 3870.42 (Iterations=7)
Stage I: Epoch 2 - Epoch Error SS = 7.98327e-28 (Iterations=58)
Stage I Training Converged at Epoch = 2


STAGE I FINAL ERROR SS = 0.000000

OPTIMUM WEIGHTS AFTER STAGE I TRAINING:
weight[0] = 2.29887     weight[1] = 4.67619     weight[2] = 5.82157
weight[3] = 2.01906     weight[4] = 3.02824     weight[5] = 5.61885
weight[6] = 9.46619     weight[7] = 7.4468      weight[8] = 1.82604
weight[9] = 6.08944     weight[10] = 11.1717    weight[11] = 5.30126
weight[12] = 2.15757    weight[13] = 2.26888    weight[14] = -0.236196
weight[15] = -3.47241   weight[16] = 0.101253   weight[17] = 2.71176
weight[18] = 6.50335

STAGE I TRAINING CONVERGED
STAGE I ERROR SS = 0.000000


GRADIENT AT THE OPTIMUM WEIGHTS
g[0] =  -0.000000        weight[0] =    2.298870
g[1] =  -0.000000        weight[1] =    4.676192
g[2] =  -0.000000        weight[2] =    5.821575
g[3] =  -0.000000        weight[3] =    2.019061
g[4] =  -0.000000        weight[4] =    3.028242
g[5] =  -0.000000        weight[5] =    5.618845
g[6] =  -0.000000        weight[6] =    9.466193
g[7] =  -0.000000        weight[7] =    7.446795
g[8] =  0.000000         weight[8] =    1.826039
g[9] =  0.000000         weight[9] =    6.089441
g[10] =         0.000000         weight[10] =   11.171695
g[11] =         0.000000         weight[11] =   5.301255
g[12] =         -0.000000        weight[12] =   2.157568
g[13] =         -0.000000        weight[13] =   2.268878
g[14] =         -0.000000        weight[14] =   -0.236196
g[15] =         -0.000000        weight[15] =   -3.472408
g[16] =         -0.000000        weight[16] =   0.101253
g[17] =         0.000000         weight[17] =   2.711758
g[18] =         -0.000000        weight[18] =   6.503353

Training Completed

Predictions for last 10 observations:
observation[90]  49.297475 Prediction  49.297475 Residual  -0.000000
observation[91]  32.435095 Prediction  32.435095 Residual   0.000000
observation[92]  37.817759 Prediction  37.817759 Residual   0.000000
observation[93]  38.506628 Prediction  38.506628 Residual   0.000000
observation[94]  48.623794 Prediction  48.623794 Residual   0.000000
observation[95]  37.623908 Prediction  37.623908 Residual   0.000000
observation[96]  41.569433 Prediction  41.569433 Residual   0.000000
observation[97]  36.828973 Prediction  36.828973 Residual  -0.000000
observation[98]  48.690826 Prediction  48.690826 Residual   0.000000
observation[99]  32.048108 Prediction  32.048108 Residual  -0.000000
Bias:  -1.39937958443962
X1:  13.670361
X2:  18.473566
X3:  13.989967
X4:  30.314709