clusterHierarchical¶

Performs a hierarchical cluster analysis given a distance matrix.

Synopsis¶

clusterHierarchical (dist)

Required Arguments¶

float dist[[]] (Input/Ouput): An npt by npt symmetric matrix containing the distance (or similarity) matrix. dist is a symmetric matrix. On input, only the upper triangular part needs to be present. The function clusterHierarchical saves the upper triangular part of dist in the lower triangle. On return from clusterHierarchical, the upper triangular part of dist is restored, and the matrix is made symmetric.

Optional Arguments¶

method, int (Input)

Option giving the clustering method to be used.

`method`	Method
0	Single linkage (minimum distance)
1	Complete linkage (maximum distance)
2	Average distance within (average distance between objects within the merged cluster)
3	Average distance between (average distance between objects in the two clusters)
4	Ward’s method (minimize the within-cluster sums of squares). For Ward’s method, the elements of `dist` are assumed to be Euclidean distances.

Default: method = 0.

transformation, int (Input)

Option giving the method to be used for clustering.

`method`	Method
0	No transformation is required. The elements of `dist` are distances.
1	Convert similarities to distances by multiplication by -1.0.
2	Convert similarities (usually correlations) to distances by taking the reciprocal of the absolute value.

Default: transformation = 0.

clusters, clevel, iclson, icrson (Output)

Argument clevel is an array of length npt - 1 containing the level at which the clusters are joined. clevel[k-1] contains the distance (or similarity) level at which cluster npt + k was formed. If the original data in dist was transformed via the optional argument transformation, the inverse transformation is applied to the values in clevel prior to exit from clusterHierarchical. Argument iclson is an array of length npt ‑ 1 containing the left sons of each merged cluster. Argument icrson is an array of length npt - 1 containing the right sons of each merged cluster. Cluster npt + k is formed by merging clusters iclson[k‑1] and icrson[k‑1].

Description¶

Function clusterHierarchical conducts a hierarchical cluster analysis based upon the distance matrix, or by appropriate use of the transformation optional argument, based upon a similarity matrix. Only the upper triangular part of the matrix dist is required as input to clusterHierarchical.

Hierarchical clustering in clusterHierarchical proceeds as follows. Initially, each data point is considered to be a cluster, numbered 1 to n = npt.

If the data matrix contains similarities, they are converted to distances by the method specified by transformation. Set \(k=1\).
A search is made of the distance matrix to find the two closest clusters. These clusters are merged to form a new cluster, numbered n + k. The cluster numbers of the two clusters joined at this stage are saved in icrson and iclson, and the distance measure between the two clusters is stored in clevel.
Based upon the method of clustering, updating of the distance measure in the row and column of dist corresponding to the new cluster is performed.
Set \(k=k+1\). If \(k<n\), go to Step 2.

The five methods differ primarily in how the distance matrix is updated after two clusters have been joined. The method optional argument specifies how the distance of the cluster just merged with each of the remaining clusters will be updated. Function clusterHierarchical allows five methods for computing the distances. To understand these measures, suppose in the following discussion that clusters “A” and “B” have just been joined to form cluster “Z”, and interest is in computing the distance of Z with another cluster called “C”.

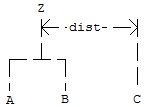
`method`	Method
0	Single linkage method. The distance from Z to C is the minimum of the distances (A to C, B to C).
1	Complete linkage method. The distance from Z to C is the maximum of the distances (A to C, B to C).
2	Average-distance-within-clusters method. The distance from Z to C is the average distance of all objects that would be within the cluster formed by merging clusters Z and C. This average may be computed according to formulas given by Anderberg (1973, page 139).
3	Average-distance-between-clusters method. The distance from Z to C is the average distance of objects within cluster Z to objects within cluster C. This average may be computed according to methods given by Anderberg (1973, page 140).
4	Ward’s method. Clusters are formed so as to minimize the increase in the within-cluster sums of squares. The distance between two clusters is the increase in these sums of squares if the two clusters were merged. A method for computing this distance from a squared Euclidean distance matrix is given by Anderberg (1973, pages 142-145).

In general, single linkage will yield long thin clusters while complete linkage will yield clusters that are more spherical. Average linkage and Ward’s linkage tend to yield clusters that are similar to those obtained with complete linkage.

Function clusterHierarchical produces a unique representation of the binary cluster tree via the following three conventions; the fact that the tree is unique should aid in interpreting the clusters. First, when two clusters are joined and each cluster contains two or more data points, the cluster that was initially formed with the smallest level (in clevel) becomes the left son. Second, when a cluster containing more than one data point is joined with a cluster containing a single data point, the cluster with the single data point becomes the right son. Finally, when two clusters containing only one object are joined, the cluster with the smallest cluster number becomes the right son.

Comments¶

The clusters corresponding to the original data points are numbered from 1 to npt. The npt - 1 clusters formed by merging clusters are numbered npt + 1 to npt + (npt - 1).
Raw correlations, if used as similarities, should be made positive and transformed to a distance measure. One such transformation can be performed by specifying optional argument transformation, with transformation = 2 in clusterHierarchical.
The user may cluster either variables or observations in clusterHierarchical since a dissimilarity matrix, not the original data, is used. Function dissimilarities may be used to compute the matrix dist for either the variables or observations.

Example¶

In the following example, the average distance within clusters method is used to perform a hierarchical cluster analysis of the Fisher Iris data. Function dataSets (see Chapter 15, Utilities) is first used to obtain the Fisher Iris data. The example is typical in that after the program obtains the data, function dissimilarities computes the distance matrix (dist) prior to calling clusterHierarchical.

from __future__ import print_function
from numpy import *
from pyimsl.stat.clusterHierarchical import clusterHierarchical
from pyimsl.stat.dataSets import dataSets
from pyimsl.stat.dissimilarities import dissimilarities

iscale = 1
ind = (1, 2, 3, 4)

x = dataSets(3)

dist = dissimilarities(x,
                       index=ind,
                       scale=iscale)

clusters = {}
clusterHierarchical(dist,
                    clusters=clusters,
                    method=2)

clevel = clusters['clevel']
for i in range(0, 149, 15):
    print("%6.2f\t" % clevel[i], end=' ')
print()
iclson = clusters['iclson']
for i in range(0, 149, 15):
    print("%6i\t" % iclson[i], end=' ')
print()
icrson = clusters['icrson']
for i in range(0, 149, 15):
    print("%6i\t" % icrson[i], end=' ')

Output¶

00	   0.17	   0.23	   0.27	   0.31	   0.37	   0.41	   0.48	   0.60	   0.78	 
   152	    100	    127	    131	    198	    186	    218	    261	    249	 
    29	     56	    124	    108	     91	    212	    243	    266	    262