clusterNumber¶
Computes cluster membership for a hierarchical cluster tree.
Synopsis¶
clusterNumber (npt, iclson, icrson, k)
Required Arguments¶
- int
npt(Input) - Number of data points to be clustered.
- int
iclson[](Input) An array of length
npt- 1 containing the left son cluster numbers.Cluster
npt+iis formed by merging clustersiclson[i-1]andicrson[i-1].- int
icrson[](Input) An array of length
npt- 1 containing the right son cluster numbers.Cluster
npt+iis formed by merging clustersiclson[i-1]andicrson[i-1].- int
k(Input) - Desired number of clusters.
Return Value¶
An array of length npt containing the cluster membership of each
observation.
Optional Arguments¶
obsPerCluster(Output)- An array of length
kcontaining the number of observations in each cluster.
Description¶
Given a fixed number of clusters (K) and the cluster tree (vectors
icrson and iclson) produced by the hierarchical clustering algorithm
(see function clusterHierarchical, function
clusterNumber determines the cluster membership of each observation. The
function clusterNumber first determines the root nodes for the K
distinct subtrees forming the K clusters and then traverses each subtree
to determine the cluster membership of each observation. The function
clusterNumber also returns the number of observations found in each
cluster.
Examples¶
Example 1¶
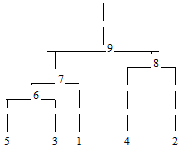
In the following example, cluster membership for \(K=2\) clusters is
found for the displayed cluster tree. The output vector iclus contains
the cluster numbers for each observation.
from numpy import *
from pyimsl.stat.clusterNumber import clusterNumber
from pyimsl.stat.writeMatrix import writeMatrix
k = 2
npt = 5
iclson = [5, 6, 4, 7]
icrson = [3, 1, 2, 8]
iclus = clusterNumber(npt, iclson, icrson, k)
writeMatrix("iclus", iclus, writeFormat="%5i")
Output¶
iclus
1 2 3 4 5
1 2 1 2 1
Example 2¶
This example illustrates the typical usage of clusterNumber. The Fisher
Iris data (see function dataSets,
Utilities) is clustered. First the distance between the
irises is computed using function dissimilarities.
The resulting distance matrix is then clustered using function
clusterHierarchical. The cluster membership for 5
clusters is then obtained via function clusterNumber using the output
from clusterHierarchical. The need for 5 clusters can be obtained either
by theoretical means or by examining a cluster tree. The cluster membership
for each of the iris observations is printed.
from numpy import *
from pyimsl.stat.clusterHierarchical import clusterHierarchical
from pyimsl.stat.clusterNumber import clusterNumber
from pyimsl.stat.dataSets import dataSets
from pyimsl.stat.dissimilarities import dissimilarities
from pyimsl.stat.randomUniform import randomUniform
from pyimsl.stat.randomSeedSet import randomSeedSet
from pyimsl.stat.writeMatrix import writeMatrix
npt = 150
ind = (1, 2, 3, 4)
k = 5
x = dataSets(3)
dist = dissimilarities(x, index=ind)
randomSeedSet(4)
for i in range(0, npt):
for j in range(i + 1, npt):
f_rand = randomUniform(1)
dist[i][j] = max(0.0, dist[i][j] + .001 * f_rand)
dist[j][i] = dist[i][j]
clusters = {}
clusterHierarchical(dist,
clusters=clusters)
iclson = clusters['iclson']
icrson = clusters['icrson']
nclus = []
iclus = clusterNumber(npt, iclson, icrson, k,
obsPerCluster=nclus)
writeMatrix('iclus', iclus, writeFormat="%5i")
writeMatrix('nclus', nclus, writeFormat="%5i")
Output¶
iclus
1 2 3 4 5 6 7 8 9 10 11
5 5 5 5 5 5 5 5 5 5 5
12 13 14 15 16 17 18 19 20 21 22
5 5 5 5 5 5 5 5 5 5 5
23 24 25 26 27 28 29 30 31 32 33
5 5 5 5 5 5 5 5 5 5 5
34 35 36 37 38 39 40 41 42 43 44
5 5 5 5 5 5 5 5 5 5 5
45 46 47 48 49 50 51 52 53 54 55
5 5 5 5 5 5 2 2 2 2 2
56 57 58 59 60 61 62 63 64 65 66
2 2 1 2 2 1 2 2 2 2 2
67 68 69 70 71 72 73 74 75 76 77
2 2 2 2 2 2 2 2 2 2 2
78 79 80 81 82 83 84 85 86 87 88
2 2 2 2 2 2 2 2 2 2 2
89 90 91 92 93 94 95 96 97 98 99
2 2 2 2 2 1 2 2 2 2 1
100 101 102 103 104 105 106 107 108 109 110
2 2 2 2 2 2 2 3 2 2 2
111 112 113 114 115 116 117 118 119 120 121
2 2 2 2 2 2 2 4 2 2 2
122 123 124 125 126 127 128 129 130 131 132
2 2 2 2 2 2 2 2 2 2 4
133 134 135 136 137 138 139 140 141 142 143
2 2 2 2 2 2 2 2 2 2 2
144 145 146 147 148 149 150
2 2 2 2 2 2 2
nclus
1 2 3 4 5
4 93 1 2 50