gammaIncomplete

Evaluates the incomplete gamma function \(\gamma(a,x)\).

Synopsis

gammaIncomplete (a, x)

Required Arguments

float a (Input)

Parameter of the incomplete gamma function is to be evaluated. It must be positive.

float x (Input)

Point at which the incomplete gamma function is to be evaluated. It must be nonnegative.

Return Value

The value of the incomplete gamma function \(\gamma(a,x)\).

Description

The incomplete gamma function, \(\gamma(a,x)\), is defined to be

\[\gamma(a,x) = \int_0^x t^{a-1} e^{-t} dt\]

for x > 0. The incomplete gamma function is defined only for a > 0. Although \(\gamma(a,x)\) is well defined for x > −∞, this algorithm does not calculate \(\gamma(a,x)\) for negative x. For large a and sufficiently large x, \(\gamma(a,x)\) may overflow. \(\gamma(a,x)\) is bounded by \(\Gamma(a)\), and users may find this bound a useful guide in determining legal values for a.

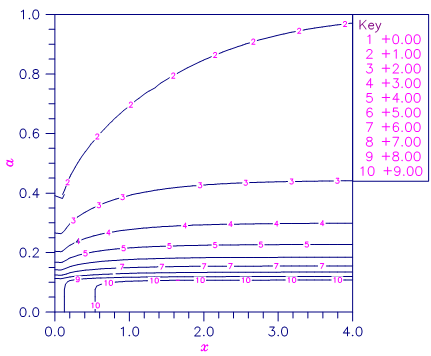
Figure 15.3 — Contour Plot of γ(a, x)

Example

Evaluates the incomplete gamma function at \(a=1\) and \(x=3\).

from __future__ import print_function
from pyimsl.stat.gammaIncomplete import gammaIncomplete

x = 3.0
a = 1.0
ans = gammaIncomplete(a, x)
print("incomplete gamma(%f,%f) = %f\n" % (a, x, ans))

Output

incomplete gamma(1.000000,3.000000) = 0.950213

Fatal Errors

IMSLS_NO_CONV_200_TS_TERMS	The function did not converge in 200 terms of Taylor series.
IMSLS_NO_CONV_200_CF_TERMS	The function did not converge in 200 terms of the continued fraction.