- java.lang.Object
-
- com.imsl.datamining.KohonenSOM
-
- All Implemented Interfaces:
- Serializable, Cloneable
public class KohonenSOM extends Object implements Serializable, Cloneable
A Kohonen self organizing map.A self-organizing map (SOM), also known as a Kohonen map or Kohonen SOM, is a technique for gathering high-dimensional data into clusters that are constrained to lie in low dimensional space, usually two dimensions. A Kohonen map is a widely used technique for the purpose of feature extraction and visualization for very high dimensional data in situations where classifications are not known beforehand. The Kohonen SOM is equivalent to an artificial neural network having inputs linked to every node in the network. Self-organizing maps use a neighborhood function to preserve the topological properties of the input space.
In a Kohonen map, nodes are arranged in a rectangular or hexagonal grid or lattice. The input is connected to each node, and the output of the Kohonen map is the zero-based (i, j) index of the node that is closest to the input. A Kohonen map involves two steps: training and forecasting. Training builds the map using input examples (vectors), and forecasting classifies a new input.
During training, an input vector is fed to the network. The input's Euclidean distance from all the nodes is calculated. The node with the shortest distance is identified and is called the Best Matching Unit, or BMU. After identifying the BMU, the weights of the BMU and the nodes closest to it in the SOM lattice are updated towards the input vector. The magnitude of the update decreases with time and with distance (within the lattice) from the BMU. The weights of the nodes surrounding the BMU are updated according to:
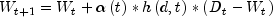
where
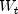 represents the node weights,
represents the node weights,
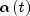 is the monotonically decreasing
learning coefficient function,
is the monotonically decreasing
learning coefficient function, 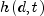 is
the neighborhood function, d is the lattice distance between the node
and the BMU, and
is
the neighborhood function, d is the lattice distance between the node
and the BMU, and 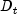 is the input vector.
is the input vector.The monotonically decreasing learning coefficient function
 is a scalar factor that defines
the size of the update correction. The value of
is a scalar factor that defines
the size of the update correction. The value of
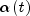 decreases with the step index
t.
decreases with the step index
t.The neighborhood function
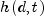 depends on the lattice distance d between the node and the BMU, and
represents the strength of the coupling between the node and BMU. In the
simplest form, the value of
depends on the lattice distance d between the node and the BMU, and
represents the strength of the coupling between the node and BMU. In the
simplest form, the value of 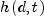 is 1
for all nodes closest to the BMU and 0 for others, but a Gaussian function
is also commonly used. Regardless of the functional form, the neighborhood
function shrinks with time (Hollmén, 15.2.1996). Early on, when the
neighborhood is broad, the self-organizing takes place on the global scale.
When the neighborhood has shrunk to just a couple of nodes, the weights
converge to local estimates.
is 1
for all nodes closest to the BMU and 0 for others, but a Gaussian function
is also commonly used. Regardless of the functional form, the neighborhood
function shrinks with time (Hollmén, 15.2.1996). Early on, when the
neighborhood is broad, the self-organizing takes place on the global scale.
When the neighborhood has shrunk to just a couple of nodes, the weights
converge to local estimates.Note that in a rectangular grid, the BMU has four closest nodes for the Von Neumann neighborhood type, or eight closest nodes for the Moore neighborhood type. In a hexagonal grid, the BMU has six closest nodes.
During training, this process is repeated for a number of iterations on all input vectors.
During forecasting, the node with the shortest Euclidean distance is the winning node, and its (i, j) index is the output.
- See Also:
- Example, Serialized Form
-
-
Field Summary
Fields Modifier and Type Field and Description static intGRID_HEXAGONALIndicates a hexagonal grid.static intGRID_RECTANGULARIndicates a rectangular grid.static intTYPE_MOOREIndicates a Moore neighborhood type.static intTYPE_VON_NEUMANNIndicates a Von Neumann neighborhood type.
-
Constructor Summary
Constructors Constructor and Description KohonenSOM(int dim, int nrow, int ncol)Constructor for aKohonenSOMobject.
-
Method Summary
Methods Modifier and Type Method and Description int[]forecast(double[] input)Returns a forecast computed using theKohonenSOMobject.int[][]forecast(double[][] input)Returns forecasts computed using theKohonenSOMobject.intgetDimension()Returns the number of weights for each node.intgetGridType()Returns the grid type.intgetNeighborhoodType()Returns the neighborhood type for the rectangular grid.intgetNumberOfColumns()Returns the number of columns of the node grid.intgetNumberOfRows()Returns the number of rows of the node grid.double[][][]getWeights()Returns the weights of the nodes.double[]getWeights(int i, int j)Returns the weights of the node at (i, j) in the node grid.booleanisWrapAround()Returns whether the opposite edges are connected or not.voidsetGridType(int type)Sets the grid type.voidsetNeighborhoodType(int type)Sets the neighborhood type.voidsetWeights()Sets the weights of the nodes using random numbers.voidsetWeights(double[][][] weights)Sets the weights of the nodes.voidsetWeights(int i, int j, double[] weights)Sets the weights of the node at (i, j) in the node grid.voidsetWeights(Random random)Sets the weights of the nodes using aRandomobject.voidwrapAround()Sets a flag to indicate the map should wrap around or connect opposite edges.
-
-
-
Field Detail
-
GRID_HEXAGONAL
public static final int GRID_HEXAGONAL
Indicates a hexagonal grid.- See Also:
- Constant Field Values
-
GRID_RECTANGULAR
public static final int GRID_RECTANGULAR
Indicates a rectangular grid.- See Also:
- Constant Field Values
-
TYPE_MOORE
public static final int TYPE_MOORE
Indicates a Moore neighborhood type.- See Also:
- Constant Field Values
-
TYPE_VON_NEUMANN
public static final int TYPE_VON_NEUMANN
Indicates a Von Neumann neighborhood type.- See Also:
- Constant Field Values
-
-
Constructor Detail
-
KohonenSOM
public KohonenSOM(int dim, int nrow, int ncol)Constructor for aKohonenSOMobject.- Parameters:
dim- Anintscalar containing the number of weights for each node in the node grid.dimmust be greater than zero.nrow- Anintscalar containing the number of rows in the node grid.nrowmust be greater than zero.ncol- Anintscalar containing the number of columns in the node grid.ncolmust be greater than zero.
-
-
Method Detail
-
forecast
public int[] forecast(double[] input)
Returns a forecast computed using theKohonenSOMobject.- Parameters:
input- Adoublearray containing the input data.input.lengthmust be equal todim.- Returns:
- An
intarray of length 2 containing the (i, j) index of the output node.
-
forecast
public int[][] forecast(double[][] input)
Returns forecasts computed using theKohonenSOMobject.- Parameters:
input- Adoublematrix containinginput.lengthobservations of data.input[i].lengthmust be equal todim.- Returns:
- An
intmatrix containing the output indices of the nodes. The i-th row contains the (i, j) index of the output node forinput[i].
-
getDimension
public int getDimension()
Returns the number of weights for each node.- Returns:
- An
intscalar containing the number of weights for each node.
-
getGridType
public int getGridType()
Returns the grid type.- Returns:
- An
intscalar containing the grid type. The return value is eitherKohonenSOM.GRID_RECTANGULARorKohonenSOM.GRID_HEXAGONAL
-
getNeighborhoodType
public int getNeighborhoodType()
Returns the neighborhood type for the rectangular grid.- Returns:
- An
intscalar containing the neighborhood type. The return value is eitherKohonenSOM.TYPE_VON_NEUMANNorKohonenSOM.TYPE_MOORE
-
getNumberOfColumns
public int getNumberOfColumns()
Returns the number of columns of the node grid.- Returns:
- An
intscalar containing the number of columns of the node grid.
-
getNumberOfRows
public int getNumberOfRows()
Returns the number of rows of the node grid.- Returns:
- An
intscalar containing the number of rows of the node grid.
-
getWeights
public double[][][] getWeights()
Returns the weights of the nodes.- Returns:
- An
nrowbyncolmatrix of double arrays containing the weights of the nodes.
-
getWeights
public double[] getWeights(int i, int j)Returns the weights of the node at (i, j) in the node grid.- Parameters:
i- Anintscalar containing the row index of the node in the node grid, where .
.j- Anintscalar containing the column index of the node in the node grid, where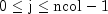 .
.- Returns:
- A
doublearray containing the weights of the node at (i, j) in the node grid.
-
isWrapAround
public boolean isWrapAround()
Returns whether the opposite edges are connected or not.- Returns:
- A
booleanindicating whether or not the opposite edges are connected. It is true if the opposite edges are connected. Otherwise, it is false.
-
setGridType
public void setGridType(int type)
Sets the grid type.- Parameters:
type- Anintscalar containing the grid type, rectangular (KohonenSOM.GRID_RECTANGULAR) or hexagonal (KohonenSOM.GRID_HEXAGONAL).Default:
type=GRID_RECTANGULAR.typeDescription GRID_RECTANGULARUse a rectangular grid ( type= 0).GRID_HEXAGONALUse a hexagonal grid ( type= 1).
-
setNeighborhoodType
public void setNeighborhoodType(int type)
Sets the neighborhood type.- Parameters:
type- Anintscalar containing the neighborhood type, Von Neumann (KohonenSOM.TYPE_VON_NEUMANN) or Moore (KohonenSOM.TYPE_MOORE). This method is ignored for a hexagonal grid.Default:
type=TYPE_VON_NEUMANN.typeDescription TYPE_VON_NEUMANNUse the Von Neumann ( type= 0) neighborhood type.TYPE_MOOREUse the Moore ( type= 1) neighborhood type.
-
setWeights
public void setWeights()
Sets the weights of the nodes using random numbers. The weights are in [0.0, 1.0].
-
setWeights
public void setWeights(double[][][] weights)
Sets the weights of the nodes.- Parameters:
weights- Annrowbyncolmatrix of double arrays containing the weights of the nodes.weights[i][j].lengthmust be equal todim.
-
setWeights
public void setWeights(int i, int j, double[] weights)Sets the weights of the node at (i, j) in the node grid.- Parameters:
i- Anintscalar containing the row index of the node in the node grid, where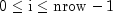 .
.j- Anintscalar containing the column index of the node in the node grid, where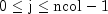 .
.weights- Adoublearray containing the weights.weights.lengthmust be equal todim.
-
setWeights
public void setWeights(Random random)
Sets the weights of the nodes using aRandomobject. The weights are generated using theRandom.nextDoublemethod.- Parameters:
random- ARandomobject used to generate random numbers for the nodes.
-
wrapAround
public void wrapAround()
Sets a flag to indicate the map should wrap around or connect opposite edges. A hexagonal grid must have an even number of rows to wrap around. By default, opposite edges are not connected.
-
-