Package com.imsl.math

package com.imsl.math
Mathematical functions and algorithms.

Differential Equations

Ordinary Differential Equations

An ordinary differential equation is an equation involving one or more dependent variables called \(y_i\), one independent variable, t, and derivatives of the \(y_i\) with respect to t.

In the initial-value problem (IVP), the initial or starting values of the dependent variables \(y_i\) at a known value \(t = t_0\) are given. Values of \(y_i(t)\) for \(t \gt t_0\) or \(t \lt t_0\) are required.

The classes OdeRungeKutta and OdeAdamsGear solve the IVP for ODEs of the form

$$\frac{{dy_i }}{{dt}} = y'_i = f_i \left( {t,\,y_1 ,\,...\,,y_N } \right)\,\,\,\,\,\,\,\,\,\,i = 1,\,...\,,\,N$$

with \(y_i(t_0)\) specified. Here, \(f_i\) is a user-supplied function that must be evaluated at any set of values \((t, y_1, \ldots, y_N), i = 1, \ldots, N\).

This problem statement is abbreviated by writing it as a system of first-order ODEs,

$$y\left( t \right) = \left[ {y_1 \left( t \right), \ldots ,y_N \left ( t \right)} \right]^T , f(t,y) = \left[ {f_1 \left( {t,y} \right), \ldots ,f_N \left( {t,y} \right)} \right]^T$$

so that the problem becomes \(y' = f\left( {t,y} \right) \) with initial values \(y(t_0)\).

The system

$$\frac{{dy}}{{dt}} = y' = f\left( {t,y} \right)$$

is said to be stiff if some of the eigenvalues of the Jacobian matrix

$$\left\{ {\partial y'_i /\partial y_j } \right\}$$

are large and negative. This is frequently the case for differential equations modeling the behavior of physical systems, such as chemical reactions proceeding to equilibrium where subspecies effectively complete their reactions in different epochs. An alternate model concerns discharging capacitors such that different parts of the system have widely varying decay rates (or time constants).

Users typically identify stiff systems by the fact that numerical differential equation solvers such as OdeRungeKutta are inefficient, or else completely fail. Special methods are often required. The most common inefficiency is that a large number of evaluations of f(t, y) (and hence an excessive amount of computer time) are required to satisfy the accuracy and stability requirements of the software. In such cases, use OdeAdamsGear. For more discussion about stiff systems, see Gear (1971, Chapter 11) or Shampine and Gear (1979).

Partial Differential Equations

The FeynmanKac class solves the Feynman-Kac equation, a single partial differential equation, on a finite interval \([x_{\min},x_{\max}]\), for given grid points on the time interval \( [ \hat{T}, T ] \). This equation often arises in applications from financial engineering and that is the primary focus of the documentation examples. The equation, initial conditions and Feynman-Kac boundary values are given by $$ f_t+\mu(x,t)+\frac{\sigma^2(x,t)}{2}f_{xx}-\kappa(x,t)f = \phi(f,x,t) $$ $$ f(x,T)=p(x) $$ $$ a(x,t)f+b(x,t)f_x+c(x,t)f_{xx}=d(x,t), \; x = x_{\min} \text{ or } x = x_{\max} $$ where $$ f_t=\frac{\partial{f}}{\partial{t}}, f_{tt}=\frac{\partial^2{f}}{(\partial{t})^2}, \text{etc.} $$

For a grid point in \([\hat{T}, T]\), the solution is approximated by a piece-wise series of Hermite quintic polynomials on a grid of the interval \([x_{\min},x_{\max}]\) that yields a twice differentiable solution.

Eigensystem Analysis

An ordinary linear eigensystem problem is represented by the equation \(Ax = \lambda x\) where A denotes an n x n matrix. The value \(\lambda\) is an eigenvalue and \(x \neq 0\) is the corresponding eigenvector. The eigenvector is determined up to a scalar factor. In all functions, we have chosen this factor so that x has Euclidean length one, and the component of x of largest magnitude is positive. If x is a complex vector, this component of largest magnitude is scaled to be real and positive. The entry where this component occurs can be arbitrary for eigenvectors having non-unique maximum magnitude values.

Error Analysis and Accuracy

Except in special cases, functions will not return the exact eigenvalue-eigenvector pair for the ordinary eigenvalue problem \(Ax = \lambda x\). Typically, the computed pair

$$\tilde x,\;\tilde \lambda$$

are an exact eigenvector-eigenvalue pair for a "nearby" matrix A + E. Information about E is known only in terms of bounds of the form \(\left\| E \right\|_2 \le f\left( n \right)\left\| A \right\|_2 \varepsilon\). The value of f(n) depends on the algorithm, but is typically a small fractional power of n. The parameter \(\varepsilon\) is the machine precision. By a theorem due to Bauer and Fike (see Golub and Van Loan 1989, p. 342),

$$\min \left| {\tilde \lambda - \lambda } \right| \le \kappa \left( X \right)\left\| E \right\|_2 \,\,\,\, {\rm{for\,\, all}} \, \lambda \, {\rm{in}} \, \sigma \left( A \right) $$

where \(\sigma(A)\) is the set of all eigenvalues of A (called the spectrum of A), X is the matrix of eigenvectors, \(\left\| \cdot \right\|_2\) is Euclidean length, and \(\kappa (X)\) is the condition number of X defined as \(\kappa \left( X \right) = \left\| X \right\|_2 \left\| {X^{ - 1} } \right\|_2\). If A is a real symmetric or complex Hermitian matrix, then its eigenvector matrix X is respectively orthogonal or unitary. For these matrices, \(\kappa(X) = 1\).

The accuracy of the computed eigenvalues

$$\tilde \lambda _j$$

and eigenvectors

$$\tilde x_j$$

can be checked by computing their performance index \(\tau\). The performance index is defined to be

$$\tau = \mathop {\max }\limits_{1 \le j \le n} \,\,\frac{{\left\| {A\tilde x_j - \tilde \lambda _j \tilde x_j } \right\|_2 }}{{n\varepsilon \left\| A \right\|_2 \left\| {\tilde x_j } \right\|_2 }}$$

where \(\varepsilon\) is again the machine precision.

The performance index \( \tau\) is related to the error analysis because

$$\left\| {E\tilde x_j } \right\|_2 = \left\| {A\tilde x_j - \tilde \lambda _j \tilde x_j } \right\|_2$$

where E is the "nearby" matrix discussed above.

While the exact value of \(\tau\) is precision and data dependent, the performance of an eigensystem analysis function is defined as excellent if \(\tau \lt 1\), good if \(1 \leq \tau \leq 100\), and poor if \(\tau \gt 100\). This is an arbitrary definition, but large values of \(\tau\) can serve as a warning that there is a significant error in the calculation.

If the condition number \(\kappa(X)\) of the eigenvector matrix X is large, there can be large errors in the eigenvalues even if \(\tau\) is small. In particular, it is often difficult to recognize near multiple eigenvalues or unstable mathematical problems from numerical results. This facet of the eigenvalue problem is often difficult for users to understand. Suppose the accuracy of an individual eigenvalue is desired. This can be answered approximately by computing the condition number of an individual eigenvalue(see Golub and Van Loan 1989, pp. 344-345). For matrices A, such that the computed array of normalized eigenvectors X is invertible, the condition number of \(\lambda_i\) is

$$\kappa _j = \left\| {e_j^T X^{ - 1} } \right\|,$$

the Euclidean length of the j-th row of \(X^{-1}\). Users can choose to compute this matrix using the class LU in "Linear Systems." An approximate bound for the accuracy of a computed eigenvalue is then given by \(\kappa _j \varepsilon \left\| A \right\|\). To compute an approximate bound for the relative accuracy of an eigenvalue, divide this bound by \(\left| {\lambda _j } \right|\).

Interpolation and Approximation

This section contains classes to interpolate and approximate data with cubic splines. Interpolation means that the fitted curve passes through all of the specified data points. An approximation spline does not have to pass through any of the data points. An approximating curve can therefore be smoother than an interpolating curve.

Cubic splines are smooth \(C^1\) or \(C^2\) fourth-order piecewise-polynomial (pp) functions. For historical and other reasons, cubic splines are the most heavily used pp functions.

This section contains five cubic spline interpolation classes and two approximation classes. These classes are derived from the base class Spline, which provides basic services, such as spline evaluation and integration.

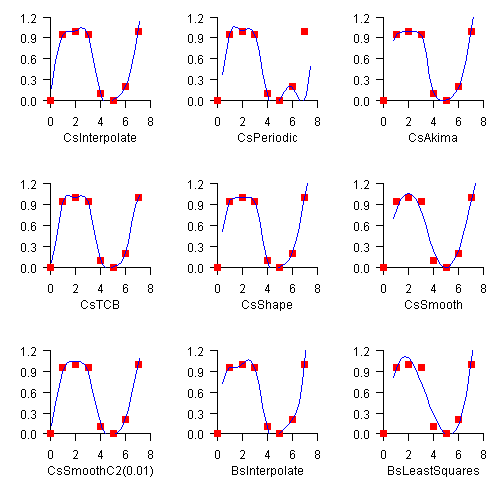
The chart shows how the nine splines in this section fit a single data set.

Class CsInterpolate allows the user to specify various endpoint conditions (such as the value of the first and second derivatives at the right and left endpoints).

Class CsPeriodic is used to fit periodic (repeating) data. The sample data set used is not periodic and so the curve does not pass through the final data point.

Class CsAkima keeps the shape of the data while minimizing oscillations.

Class CsTCB allows the user to specify various data point parameters (such as tension, continuity, and bias).

Class CsShape keeps the shape of the data by preserving its convexity.

Class CsSmooth constructs a smooth spline from noisy data.

Class CsSmoothC2 constructs a smooth spline from noisy data using cross-validation and a user-supplied smoothing parameter.

Class BSpline is the abstract base class for univariate B-splines. B-splines provide a particularly convenient and suitable basis for a given class of smooth piecewise polynomial (ppoly) functions. Such a class is specified by giving its breakpoint sequence, its order k, and the required smoothness across each of the interior breakpoints. The corresponding B-spline basis is specified by giving its knot sequence \({\bf t} \in {\bf R}\). The specification rule is as follows: if the class is to have all derivatives up to and including the j-th derivative continuous across the interior breakpoint \(\xi_i\), then the number \(\xi_i\) should occur k-j-1 times in the knot sequence. Assuming that \(\xi_0\) and \(\xi_{n-1}\) are the endpoints of the interval of interest, choose the first k knots equal to \(\xi_0\) and the last k knots equal to \(\xi_{n-1}\). This can be done because the B-splines are defined to be right continuous near \(\xi_0\) and left continuous near \(\xi_{n-1}\).

When the above construction is completed, a knot sequence t of length M is generated, and there are m = M-k B-splines of order k, for example \(B_0, \ldots, B_{m-1}\), spanning the ppoly functions on the interval with the indicated smoothness. That is, each ppoly function in this class has a unique representation \(p = a_0 B_0 + a_1 B_1 + \cdots + a_{m-1} B_{m-1}\) as a linear combination of B-splines. A B-spline is a particularly compact ppoly function. \(B_i\) is a nonnegative function that is nonzero only on the interval \([{\bf t}_i, {\bf t}_{i+k}]\) More precisely, the support of the i-th B-spline is \([{\bf t}_i, {\bf t}_{i+k}]\). No ppoly function in the same class (other than the zero function) has smaller support (i.e., vanishes on more intervals) than a B-spline. This makes B-splines particularly attractive basis functions since the influence of any particular B-spline coefficient extends only over a few intervals. When it is necessary to emphasize the dependence of the B-spline on its parameters, we will use the notation \(B_{i,k,t}\) to denote the i-th B-spline of order k for the knot sequence t.

Class BsInterpolate extends BSpline and creates a B-spline by interpolating data points.

Class BsLeastSquares extends BSpline and creates a B-spline by computing a least squares spline approximation to data points.

Class Spline2D is the abstract base class for the two-dimensional, tensor-product splines.

Class Spline2DInterpolate computes a Spline2D using interpolation from two-dimensional, tensor-product data.

Class Spline2DLeastSquares computes a Spline2D using least squares.

Class RadialBasis computes an approximation to scattered data in \({\bf R}^M\) using radial-basis functions.

Nonlinear Equations

Zeros of a Polynomial

A polynomial function of degree n can be expressed as follows:

$$p(z) = a_nz^n + a_{n-1} z^{n-1} + \dots + a_1z + a_0$$

where \(a_n \neq 0\). The class ZeroPolynomial finds zeros of a polynomial with real or complex coefficients using Aberth's method.

Zeros of a Function

The class ZerosFunction uses Muller's method to find the real zeros of a real-valued function.

Root of System of Equations

A system of equations can be stated as follows:

$$ f_i(x) = 0, {\rm for}\,\,\,\,i = 1, 2, \ldots, n $$

where \(x \in {\bf R}^n\), and \(f_i : {\bf R^n \rightarrow R} \). The ZeroSystem class uses a modified hybrid method due to M.J.D. Powell to find the zero of a system of nonlinear equations.

Optimization

Unconstrained Minimization

The unconstrained minimization problem can be stated as follows:

$$\mathop {\min }\limits_{x\; \in \;R^n } f\left( x \right)$$

where \(f : {\bf R}^ {\it n} \rightarrow {\bf R}\) is continuous and has derivatives of all orders required by the algorithms. The functions for unconstrained minimization are grouped into three categories: univariate functions, multivariate functions, and nonlinear least-squares functions.

For the univariate functions, it is assumed that the function is unimodal within the specified interval. For discussion on unimodality, see Brent (1973).

The class MinUnconMultiVar finds the minimum of a multivariate function using a quasi-Newton method. The default is to use a finite-difference approximation of the gradient of f(x). Here, the gradient is defined to be the vector

$$\nabla f\left( x \right) = \left[ {\frac{{\partial f\left( x \right)}} {{\partial x_1 }},\;\frac{{\partial f\left( x \right)}}{{\partial x_2 }},\;...\,,\;\frac{{\partial f\left( x \right)}}{{\partial x_n }}} \right]$$

However, when the exact gradient can be easily provided, the gradient should be provided by implementing the interface MinUnconMultiVar.Gradient. The NumericalDerivatives class can also be used in computing the gradient for MinUnconMultiVar as well as other classes. For an example, see NumericalDerivatives Example 6.

The nonlinear least-squares function uses a modified Levenberg-Marquardt algorithm. The most common application of the function is the nonlinear data-fitting problem where the user is trying to fit the data with a nonlinear model.

These functions are designed to find only a local minimum point. However, a function may have many local minima. Try different initial points and intervals to obtain a better local solution.

Linearly Constrained Minimization

The linearly constrained minimization problem can be stated as follows:

$$\begin{array}{c} \mathop {\min }\limits_{x\; \in \;R^n } f\left( x \right) \\ {\rm{subject \, to}} \\ A_1 x = b_1 \\ A_2 x \le b_2 \end{array}$$

where \(f : {\bf R}^{\it n} \rightarrow {\bf R}\), \(A_1\) and \(A_2\) are coefficient matrices, and \(b_1\) and \(b_2\) are vectors. If f(x) is linear, then the problem is a linear programming problem. If f(x) is quadratic, the problem is a quadratic programming problem.

The class SparseLP uses an infeasible primal-dual interior-point method to solve sparse linear programming problems of all sizes. The constraint matrix is stored in sparse coordinate storage format.

The class DenseLP uses an active set strategy to solve small- to medium-sized linear programming problems. No sparsity is assumed since the coefficients are stored in full matrix form.

The class QuadraticProgramming is designed to solve convex quadratic programming problems using a dual quadratic programming algorithm. If the given Hessian is not positive definite, then QuadraticProgramming modifies it to be positive definite. In this case, output should be interpreted with care because the problem has been changed slightly. Here, the Hessian of f(x) is defined to be the n x n matrix

$$\nabla ^2 f\left( x \right) = \left[ {\frac{{\partial ^2 }} {{\partial x_i \partial x_j }}f\left( x \right)} \right] $$

The class MinConGenLin uses Powell's TOLMIN algorithm to solve linear constrained problems for more general objective functions (beyond linear and quadratic functions).

Nonlinearly Constrained Minimization

The nonlinearly constrained minimization problem can be stated as follows:

$$\begin{array}{l} \mathop {\min }\limits_{x\; \in \;R^n } f\left( x \right) \\ {\rm{subject \, to}} \,\,\, g_i \left( x \right) = 0 \,\,\,\, {\rm{for}} \,\,\, i = 1,\;2,\;\ldots\,,\;m_1 \\ g_i \left( x \right) \ge 0 \,\,\,\, {\rm{for}} \,\,\, i = m_1 + 1,\;\ldots\,,\;m \\ \end{array}$$

where \(f : {\bf R}^{\it n} \rightarrow \bf R\) and \(g_i : {\bf R}^{\it n} \rightarrow \bf R\), for \(i = 1, 2, \ldots, m\).

The class MinConNLP uses a sequential equality constrained quadratic programming algorithm to solve this problem. A more complete discussion of this algorithm can be found in the documentation.

Return Values from User-Supplied Functions

All values returned by user-supplied functions must be valid real numbers. It is the user's responsibility to check that the values returned by a user-supplied function do not contain NaN, infinity, or negative infinity values.

Example: Minimum of a smooth function

The minimum of \(e^x - 5x\) is found using function evaluations only.

import com.imsl.math.*;

public class OptimizationIntroEx1 {
    public static void main(String args[]) {
        MinUncon zf = new MinUncon();
        zf.setGuess(0.0);
        zf.setAccuracy(0.001);
        MinUncon.Function fcn = new MinUncon.Function() {
            public double f(double x) {
                double y = StrictMath.exp(x) - 5.*x;
                if(!Double.isNaN(y)) {
                       return y;
                } else {
                       return 0.0;
                }
            }
        };
        System.out.println("Minimum is " + zf.computeMin(fcn));
    }
}

Transforms

Fast Fourier Transforms

A fast Fourier transform (FFT) is simply a discrete Fourier transform that is computed efficiently. Basically, the straightforward method for computing the Fourier transform takes approximately \(n^2\) operations where n is the number of points in the transform, while the FFT (which computes the same values) takes approximately \( n\log n \) operations. The algorithms in this section are modeled on the Cooley-Tukey (1965) algorithm. Hence, these functions are most efficient for integers that are highly composite; that is, integers that are a product of small primes.

For the two classes, FFT and ComplexFFT, a single instance can be used to transform multiple sequences of the same length. In this situation, the constructor computes the initial setup once. This may result in substantial computational savings. For more information on the use of these classes consult the documentation under the appropriate class name.

Continuous Versus Discrete Fourier Transform

There is, of course, a close connection between the discrete Fourier transform and the continuous Fourier transform. Recall that the continuous Fourier transform is defined (Brigham 1974) as

$$\hat f\left( \omega \right) = \left( {\Im f} \right)\left( \omega \right) = \int_{ - \infty }^\infty {f\left( t \right)} e^{ - 2\pi i\omega t} dt $$

We begin by making the following approximation:

$$\hat f\left( \omega \right) \approx \int_{ - T/2}^{T/2} {f\left( t \right)} e^{ - 2\pi i\omega t} dt$$

$$= \int_0^T {f\left( {t - T/2} \right)} e^{ - 2\pi i\omega \left( {t - T/2} \right)} dt$$

$$= e^{\pi i\omega T} \int_0^T {f\left( {t - T/2} \right)} e^{ - 2\pi i\omega t} dt$$

If we approximate the last integral using the rectangle rule with spacing \(h = T / n\) , we have

$$\hat f\left( \omega \right) \approx e^{\pi i\omega T} h\sum\limits_{k = 0}^{n - 1} {e^{ - 2\pi i\omega kh} } f\left( {kh - T/2} \right) $$

Finally, setting \(\omega = j/T\) for \(j = 0, \dots, n - 1\,\,\, \) yields

$$\hat f\left( {j/T} \right) \approx e^{\pi ij} h\sum\limits_{k = 0}^{n - 1} {e^{ - 2\pi ijk/n} } f\left( {kh - T/2} \right) = \left( { - 1} \right)^j \sum\limits_{k = 0}^{n - 1} {e^{ - 2\pi ijk/n} } f_k^h $$

where \(f_k^h\) denotes the \(k\)-th component of the vector \(f^h = (f(-T/2), \dots, f( (n - 1)h - T/2))\) . Thus, after scaling the components by \((-1)^h\) , the discrete Fourier transform, as computed in ComplexFFT (with input \(f^h \) ) is related to an approximation of the continuous Fourier transform by the above formula.