| SuperLU Class |
Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The SuperLU type exposes the following members.
| Name | Description | |
|---|---|---|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetPerformanceTuningParameters |
Returns a performance tuning parameter value.
| |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| SetPerformanceTuningParameters |
Sets performance tuning parameters.
| |
| Solve |
Computation of the solution vector for the system | |
| SolveTranspose |
Computation of the solution vector for the system | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| ColumnOrderingMethod |
The method used to permute the columns of the
input matrix.
| |
| ConditionNumber |
The estimate of the reciprocal condition number of the matrix
A.
| |
| DiagonalPivotThreshold |
The threshold used for a diagonal entry to be an acceptable pivot.
| |
| Equilibrate |
Specifies if input matrix A is equilibrated before factorization.
| |
| EquilibrationMethod |
The type of equilibration used before matrix factorization.
| |
| ForwardErrorBound |
The estimated forward error bound for the solution vector.
| |
| IterativeRefinement |
The iterative refinement option.
| |
| PivotGrowth |
Specifies whether to compute the reciprocal pivot growth factor.
| |
| ReciprocalPivotGrowthFactor |
The reciprocal pivot growth factor.
| |
| RelativeBackwardError |
The componentwise relative backward error of the solution vector.
| |
| SymmetricMode |
The symmetric mode option.
|
Consider the sparse linear system of equations
Gaussian elimination, applied to the system above, can be shortly described as follows:
1. Compute a triangular factorization ![]() .
Here,
.
Here, ![]() and
and ![]() are positive
definite diagonal matrices to equilibrate the system and
are positive
definite diagonal matrices to equilibrate the system and ![]() and
and ![]() are permutation matrices to ensure
numerical stability and preserve sparsity. L is a unit lower triangular
matrix and U is an upper triangular matrix.
are permutation matrices to ensure
numerical stability and preserve sparsity. L is a unit lower triangular
matrix and U is an upper triangular matrix.
2. Solve ![]() by evaluating
by evaluating
Class SuperLU handles step 1 above in the Solve
method if it has not been computed prior to step 2. More
precisely, before ![]() is solved the following steps
are performed:
is solved the following steps
are performed:
- Equilibrate matrix A, i.e. compute diagonal matrices
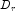 and
and 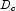 so that
so that
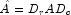 is "better conditioned" than
A, i.e.
is "better conditioned" than
A, i.e. 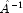 is less sensitive to
perturbations in
is less sensitive to
perturbations in 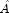 than
than
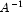 is to perturbations in A.
is to perturbations in A.
- Order the columns of
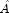 to increase the
sparsity of the computed L and U factors, i.e. replace
to increase the
sparsity of the computed L and U factors, i.e. replace
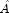 by
by 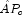 where
where
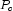 is a column permutation matrix.
is a column permutation matrix.
- Compute the LU factorization of
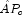 .
For numerical stability, the rows of
.
For numerical stability, the rows of 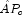 are eventually permuted through the factorization process by scaled
partial pivoting, leading to the decomposition
are eventually permuted through the factorization process by scaled
partial pivoting, leading to the decomposition
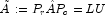 . The LU
factorization is done by a left looking supernode-panel algorithm with
2-D blocking. See Demmel, Eisenstat, Gilbert et al. (1999) for further
information on this technique.
. The LU
factorization is done by a left looking supernode-panel algorithm with
2-D blocking. See Demmel, Eisenstat, Gilbert et al. (1999) for further
information on this technique.
- Compute the reciprocal pivot growth factor
where
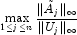
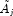 and
and 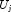 denote the
j-th column of matrices
denote the
j-th column of matrices 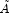 and U, respectively.
and U, respectively.
- Estimate the reciprocal of the condition number of matrix
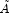 .
.
- Solve the system
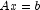 using the computed
triangular factors.
using the computed
triangular factors.
- Iteratively refine the solution, again using the computed triangular factors. This is equivalent to Newton's method.
- Compute forward and backward error bounds for the solution vector x.
Some of the steps mentioned above are optional. Their settings can be controlled by the Set methods and properties of class SuperLU.
Class SuperLU is based on the SuperLU code written by Demmel, Gilbert, Li et al. For more detailed explanations of the factorization and solve steps, see the SuperLU Users' Guide (1999).
Copyright (c) 2003, The Regents of the University of California, through Lawrence Berkeley National Laboratory (subject to receipt of any required approvals from U.S. Dept. of Energy)
All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
(1) Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
(2) Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
(3) Neither the name of Lawrence Berkeley National Laboratory, U.S. Dept. of Energy nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.