public virtual int NextNegativeBinomial(
	double rk,
	double p
)

Public Overridable Function NextNegativeBinomial ( 
	rk As Double,
	p As Double
) As Integer

public:
virtual int NextNegativeBinomial(
	double rk, 
	double p
)

abstract NextNegativeBinomial : 
        rk : float * 
        p : float -> int 
override NextNegativeBinomial : 
        rk : float * 
        p : float -> int 

Parameters

rk

Type: SystemDouble
A double which specifies the negative binomial parameter, .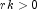

p

Type: SystemDouble
A double which specifies the probability of success on each trial. It must be greater than machine precision and less than one.

Return Value

Method NextNegativeBinomial generates pseudorandom numbers from a negative Binomial distribution with parameters and . and must be positive and p must be less than 1. The probability function with ( and ) is

for .

If r is an integer, the distribution is often called the Pascal distribution and can be thought of as modeling the length of a sequence of Bernoulli trials until r successes are obtained, where p is the probability of getting a success on any trial. In this form, the random variable takes values r, r + 1, and can be obtained from the negative binomial random variable defined above by adding r to the negative binomial variable. This latter form is also equivalent to the sum of r geometric random variables defined as taking values .

If rp/(1 - p) is less than 100 and is greater than the machine epsilon, NextNegativeBinomial uses the inverse CDF technique; otherwise, for each negative binomial deviate, NextNegativeBinomial generates a gamma (r, p/(1 - p)) deviate y and then generates a Poisson deviate with parameter y.

Reference

Other Resources