CrossCorrelation Class

Computes the sample cross-correlation function of two stationary time series.

Inheritance Hierarchy

SystemObject
Imsl.StatCrossCorrelation

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

C++

Copy

[SerializableAttribute]
public class CrossCorrelation

<SerializableAttribute>
Public Class CrossCorrelation

[SerializableAttribute]
public ref class CrossCorrelation

[<SerializableAttribute>]
type CrossCorrelation =  class end

The CrossCorrelation type exposes the following members.

Constructors

	Name	Description
	CrossCorrelation	Constructor to compute the sample cross-correlation function of two stationary time series.

Top

Methods

	Name	Description
	Equals	Determines whether the specified object is equal to the current object. (Inherited from Object.)
	Finalize	Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.)
	GetAutoCorrelationX	Returns the autocorrelations of the time series x.
	GetAutoCorrelationY	Returns the autocorrelations of the time series y.
	GetAutoCovarianceX	Returns the autocovariances of the time series x.
	GetAutoCovarianceY	Returns the autocovariances of the time series y.
	GetCrossCorrelations	Returns the cross-correlations between the time series x and y.
	GetCrossCovariances	Returns the cross-covariances between the time series x and y.
	GetHashCode	Serves as a hash function for a particular type. (Inherited from Object.)
	GetStandardErrors	Returns the standard errors of the cross-correlations between the time series x and y.
	GetType	Gets the Type of the current instance. (Inherited from Object.)
	MemberwiseClone	Creates a shallow copy of the current Object. (Inherited from Object.)
	ToString	Returns a string that represents the current object. (Inherited from Object.)

Top

Properties

	Name	Description
	MeanX	Estimate of the mean of time series x.
	MeanY	Estimate of the mean of time series y.
	NumberOfProcessors	Perform the parallel calculations with the maximum possible number of processors set to NumberOfProcessors.
	VarianceX	Returns the variance of time series x.
	VarianceY	Returns the variance of time series y.

Top

Remarks

CrossCorrelation estimates the cross-correlation function of two jointly stationary time series given a sample of n = x.Length observations $\{X_t\}$ and $\{Y_t\}$ for t = 1,2, ..., n.

Let

$\hat \mu _x = \rm{xmean}$

be the estimate of the mean $\mu _X$ of the time series $\{X_t\}$ where

$\hat \mu _X = \left\{ \begin{array}{ll} \mu _X & {\rm for}\;\mu _X\; {\rm known} \\ \frac{1}{n}\sum\limits_{t=1}^n {X_t } & {\rm for}\; \mu _X\; {\rm unknown} \end{array} \right.$

The autocovariance function of $\{X_t\}$ , $\sigma _X(k)$ , is estimated by

$\hat \sigma _X\left( k \right) = \frac{1}{n} \sum\limits_{t = 1}^{n - k} {\left( {X_t - \hat \mu _X} \right)} \left( {X_{t + k} - \hat \mu _X} \right), \mbox{\hspace{20pt}k=0,1,\dots,K}$

where K = maximumLag. Note that $\hat \sigma _X(0)$ is equivalent to the sample variance of x returned by property VarianceX. The autocorrelation function $\rho _X(k)$ is estimated by

$\hat\rho _X(k) = \frac{\hat \sigma _X(k)}{\hat \sigma _X(0)},\mbox{\hspace{20pt}} k=0,1,\dots,K$

Note that $\hat \rho _x(0) \equiv 1$ by definition. Let

$\hat \mu _Y = {\rm ymean}, \hat \sigma _Y(k), {\rm and} \hat \rho _Y(k)$

be similarly defined.

The cross-covariance function $\sigma _{XY}(k)$ is estimated by

$\hat \sigma _{XY}(k) = \left\{ \begin{array}{ll} \frac{1}{n}\sum\limits_{t=1}^{n-k}(X_t - {\hat \mu _X})(Y_{t+k} - {\hat\mu _Y}) & {k = 0,1, \dots,K} \\ \frac{1}{n}\sum\limits_{t=1-k}^{n}(X_t - {\hat \mu _X})(Y_{t+k} - {\hat\mu _Y}) &{k = -1,-2, \dots,-K} \end {array} \right.$

The cross-correlation function $\rho _{XY}(k)$ is estimated by

$\hat \rho _{XY}(k) = \frac{\hat \sigma _{XY}(k)} {[\hat\sigma _X(0) \hat\sigma _Y(0) ]^{\frac{1}{2}}} \;\;\; {k = 0,\pm1, \dots,\pm K}$

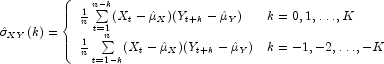
The standard errors of the sample cross-correlations may be optionally computed according to the GetStandardErrors method argument stderrMethod. One method is based on a general asymptotic expression for the variance of the sample cross-correlation coefficient of two jointly stationary time series with independent, identically distributed normal errors given by Bartlet (1978, page 352). The theoretical formula is

$\begin{array}{c} {\rm var} \left \{ \hat \rho _{XY}(k) \right \} = \frac{1}{n-k}\sum\limits_{i=-\infty}^{\infty} \left [\right. {\rho _X(i)}+\rho _{XY}(i-k)\rho _{XY}(i+k) \\ -2\rho _{XY}(k)\{\rho _X(i)\rho _{XY}(i+k)+\rho _{XY}(-i)\rho _Y(i+k)\} \\ +\rho^2_{XY}(k)\{\rho_X(i) + \frac{1}{2}\rho^2_X(i) + \frac{1}{2}\rho^2_Y(i)\} \left. \right ] \end{array}$

For computational purposes, the autocorrelations $\rho_X(k)$ and $\rho_Y(k)$ and the cross-correlations $\rho _{XY}(k)$ are replaced by their corresponding estimates for $\left|k\right|\le K$ , and the limits of summation are equal to zero for all k such that $\left|k\right| > K$ .

A second method evaluates Bartlett's formula under the additional assumption that the two series have no cross-correlation. The theoretical formula is

${\rm var}\{\hat \rho_{XY}(k)\} = \frac{1}{n-k}\sum\limits_{i=-\infty}^{\infty}{\rho_X(i)\rho_Y(i)} \;\;\;\;\; {k \ge 0}$

For additional special cases of Bartlett's formula, see Box and Jenkins (1976, page 377).

An important property of the cross-covariance coefficient is $\sigma _{XY}(k) = \sigma _{YX}(-k)$ for $k \ge 0$ . This result is used in the computation of the standard error of the sample cross-correlation for lag $k \lt 0$ . In general, the cross-covariance function is not symmetric about zero so both positive and negative lags are of interest.

Reference

Imsl.Stat Namespace

Other Resources

Example