|
Class Summary |
| Bessel |
Collection of Bessel functions. |
| BoundedLeastSquares |
Solves a nonlinear least-squares problem subject to bounds on the variables
using a modified Levenberg-Marquardt algorithm. |
| BoundedVariableLeastSquares |
Solve a linear least-squares problem with bounds on the variables. |
| BsInterpolate |
Extension of the BSpline class to interpolate data points. |
| BsLeastSquares |
Extension of the BSpline class to compute a least squares spline approximation
to data points. |
| BSpline |
BSpline represents and evaluates univariate B-splines. |
| Cholesky |
Cholesky factorization of a matrix of type double. |
| Complex |
Set of mathematical functions for complex numbers. |
| ComplexFFT |
Complex FFT. |
| ComplexLU |
LU factorization of a matrix of type Complex. |
| ComplexMatrix |
Complex matrix manipulation functions. |
| ComplexSparseCholesky |
Sparse Cholesky factorization of a matrix of type ComplexSparseMatrix. |
| ComplexSparseCholesky.NumericFactor |
Data structures and functions for the numeric Cholesky factor. |
| ComplexSparseCholesky.SymbolicFactor |
Data structures and functions for the symbolic Cholesky factor. |
| ComplexSparseMatrix |
Sparse matrix of type Complex. |
| ComplexSparseMatrix.SparseArray |
The SparseArray class uses public fields to hold
the data for a sparse matrix in the Java Sparse Array format. |
| ComplexSuperLU |
Computes the LU factorization of a general sparse matrix of type
ComplexSparseMatrix by a column method and solves a sparse
linear system of equations 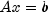 . . |
| ConjugateGradient |
Solves a real symmetric definite linear system using the conjugate gradient
method with optional preconditioning. |
| CsAkima |
Extension of the Spline class to handle the Akima cubic spline. |
| CsInterpolate |
Extension of the Spline class to interpolate data points. |
| CsPeriodic |
Extension of the Spline class to interpolate data points with
periodic boundary conditions. |
| CsShape |
Extension of the Spline class to interpolate data points consistent
with the concavity of the data. |
| CsSmooth |
Extension of the Spline class to construct a smooth cubic spline
from noisy data points. |
| CsSmoothC2 |
Extension of the Spline class used to construct a spline for noisy data
points using an alternate method. |
| CsTCB |
Extension of the Spline class to handle a tension-continuity-bias (TCB) cubic spline,
also known as a Kochanek-Bartels spline and is a generalization of the Catmull-Rom spline. |
| DenseLP |
Solves a linear programming problem using an active set strategy. |
| Eigen |
Collection of Eigen System functions. |
| EpsilonAlgorithm |
The class is used to determine the limit of a sequence of
approximations, by means of the Epsilon algorithm of
P. |
| FeynmanKac |
Solves the generalized Feynman-Kac PDE. |
| FFT |
FFT functions. |
| GenMinRes |
Linear system solver using the restarted Generalized Minimum Residual (GMRES)
method. |
| Hyperbolic |
Pure Java implementation of the hyperbolic functions and their inverses. |
| HyperRectangleQuadrature |
HyperRectangleQuadrature integrates a function over a hypercube. |
| IEEE |
Pure Java implementation of the IEEE 754 functions
as specified in IEEE Standard for Binary Floating-Point Arithmetic,
ANSI/IEEE Standard 754-1985 (IEEE, New York). |
| JMath |
Pure Java implementation of the standard java.lang.Math class. |
| LU |
LU factorization of a matrix of type double. |
| Matrix |
Matrix manipulation functions. |
| MinConGenLin |
Minimizes a general objective function subject to linear equality/inequality
constraints. |
| MinConNLP |
General nonlinear programming solver. |
| MinUncon |
Unconstrained minimization. |
| MinUnconMultiVar |
Unconstrained multivariate minimization. |
| NonlinLeastSquares |
Nonlinear least squares. |
| NonNegativeLeastSquares |
Solves a linear least squares problem with nonnegativity constraints. |
| NumericalDerivatives |
Compute the Jacobian matrix for a function 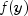 with
m components in n independent variables. with
m components in n independent variables. |
| ODE |
ODE represents and solves an initial-value problem for ordinary differential
equations. |
| OdeAdamsGear |
Extension of the ODE class to solve a stiff initial-value problem for
ordinary differential equations using the Adams-Gear methods. |
| OdeRungeKutta |
Solves an initial-value problem for ordinary differential
equations using the Runge-Kutta-Verner fifth-order and
sixth-order method. |
| Physical |
Return the value of various mathematical and physical constants. |
| PrintMatrix |
Matrix printing utilities. |
| PrintMatrixFormat |
This class can be used to customize the actions of PrintMatrix. |
| QR |
QR Decomposition of a matrix. |
| QuadraticProgramming |
Solves the convex quadratic programming problem subject to equality or inequality
constraints. |
| Quadrature |
Quadrature is a general-purpose integrator that uses a globally
adaptive scheme in order to reduce the absolute error. |
| RadialBasis |
RadialBasis computes a least-squares fit to scattered data in 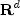 , where d is the dimension. , where d is the dimension. |
| RadialBasis.Gaussian |
The Gaussian basis function, 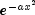 . . |
| RadialBasis.HardyMultiquadric |
The Hardy multiquadric basis function, 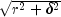 . . |
| Sfun |
Collection of special functions. |
| SparseCholesky |
Sparse Cholesky factorization of a matrix of type SparseMatrix. |
| SparseCholesky.NumericFactor |
The numeric Cholesky factorization of a matrix. |
| SparseCholesky.SymbolicFactor |
The symbolic Cholesky factorization of a matrix. |
| SparseMatrix |
Sparse matrix of type double. |
| SparseMatrix.SparseArray |
The SparseArray class uses public fields to hold
the data for a sparse matrix in the Java Sparse Array format. |
| Spline |
Spline represents and evaluates univariate piecewise polynomial splines. |
| Spline2D |
Represents and evaluates tensor-product splines. |
| Spline2DInterpolate |
Computes a two-dimensional, tensor-product spline interpolant from
two-dimensional, tensor-product data. |
| Spline2DLeastSquares |
Computes a two-dimensional, tensor-product spline approximant using least squares. |
| SuperLU |
Computes the LU factorization of a general sparse matrix of type
SparseMatrix by a column method and solves the real sparse linear
system of equations 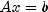 . . |
| SVD |
Singular Value Decomposition (SVD) of a
rectangular matrix of type double. |
| SymEigen |
Computes the eigenvalues and eigenvectors of a real
symmetric matrix. |
| ZeroPolynomial |
The ZeroPolynomial class computes the zeros of a polynomial
with complex coefficients, Aberth's method. |
| ZerosFunction |
Finds the real zeros of a real, continuous, univariate function,
f(x). |
| ZeroSystem |
Solves a system of n nonlinear equations f(x) = 0 using a modified Powell
hybrid algorithm. |
|
Exception Summary |
| BoundedLeastSquares.FalseConvergenceException |
False convergence - The iterates appear to be converging to a
noncritical point. |
| BoundedLeastSquares.NoProgressException |
The algorithm is not making any progress, try new initial guess. |
| BoundedVariableLeastSquares.TooManyIterException |
Maximum number of iterations exceeded. |
| Cholesky.NotSPDException |
The matrix is not symmetric, positive definite. |
| ComplexSparseCholesky.NotSPDException |
The matrix is not Hermitian, positive definite. |
| ConjugateGradient.NoConvergenceException |
The conjugate gradient method did not converge within the allowed maximum
number of iterations. |
| ConjugateGradient.NotDefiniteAMatrixException |
The input matrix A is indefinite, that is the matrix is not positive or
negative definite. |
| ConjugateGradient.NotDefiniteJacobiPreconditionerException |
The Jacobi preconditioner is not strictly positive or negative definite. |
| ConjugateGradient.NotDefinitePreconditionMatrixException |
The Precondition matrix is indefinite. |
| ConjugateGradient.SingularPreconditionMatrixException |
The Precondition matrix is singular. |
| CsShape.TooManyIterationsException |
Too many iterations. |
| DenseLP.AllConstraintsNotSatisfiedException |
All constraints are not satisfied. |
| DenseLP.BoundsInconsistentException |
The bounds given are inconsistent. |
| DenseLP.CyclingOccurringException |
The algorithm appears to be cycling. |
| DenseLP.MultipleSolutionsException |
The problem has multiple solutions giving essentially the same
minimum. |
| DenseLP.NoAcceptablePivotException |
No acceptable pivot could be found. |
| DenseLP.ProblemUnboundedException |
The problem is unbounded. |
| DenseLP.ProblemVacuousException |
The problem is vaxuous. |
| DenseLP.SomeConstraintsDiscardedException |
Some constraints were discarded because they were too linearly
dependent on other active constraints. |
| Eigen.DidNotConvergeException |
The iteration did not converge |
| FeynmanKac.BoundaryInconsistentException |
The boundary conditions are inconsistent. |
| FeynmanKac.ConstraintsInconsistentException |
The constraints are inconsistent. |
| FeynmanKac.CorrectorConvergenceException |
Corrector failed to converge. |
| FeynmanKac.ErrorTestException |
Error test failure detected. |
| FeynmanKac.InitialConstraintsException |
The constraints at the initial point are inconsistent. |
| FeynmanKac.IterationMatrixSingularException |
Iteration matrix is singular. |
| FeynmanKac.TcurrentTstopInconsistentException |
The end value for the integration in time, tout, is not consistent with
the current time value, t. |
| FeynmanKac.TEqualsToutException |
The current integration point in time and the end point are equal. |
| FeynmanKac.TimeIntervalTooSmallException |
Distance between starting time point and end point for the integration is
too small. |
| FeynmanKac.ToleranceTooSmallException |
Tolerance is too small. |
| FeynmanKac.TooManyIterationsException |
Too many iterations required by the DAE solver. |
| GenMinRes.TooManyIterationsException |
Maximum number of iterations exceeded. |
| MinConGenLin.ConstraintsInconsistentException |
The equality constraints are inconsistent. |
| MinConGenLin.ConstraintsNotSatisfiedException |
No vector x satisfies all of the constraints. |
| MinConGenLin.EqualityConstraintsException |
the variables are determined by the equality constraints. |
| MinConGenLin.VarBoundsInconsistentException |
The equality constraints and the bounds on the variables are found to be inconsistent. |
| MinConNLP.BadInitialGuessException |
Penalty function point infeasible for original problem. |
| MinConNLP.ConstraintEvaluationException |
Constraint evaluation returns an error with current point. |
| MinConNLP.IllConditionedException |
Problem is singular or ill-conditioned. |
| MinConNLP.LimitingAccuracyException |
Limiting accuracy reached for a singular problem. |
| MinConNLP.LinearlyDependentGradientsException |
Working set gradients are linearly dependent. |
| MinConNLP.NoAcceptableStepsizeException |
No acceptable stepsize in [SIGMA,SIGLA]. |
| MinConNLP.ObjectiveEvaluationException |
Objective evaluation returns an error with current point. |
| MinConNLP.PenaltyFunctionPointInfeasibleException |
Penalty function point infeasible. |
| MinConNLP.QPInfeasibleException |
QP problem seemingly infeasible. |
| MinConNLP.SingularException |
Problem is singular. |
| MinConNLP.TerminationCriteriaNotSatisfiedException |
Termination criteria are not satisfied. |
| MinConNLP.TooManyIterationsException |
Maximum number of iterations exceeded. |
| MinConNLP.TooMuchTimeException |
Maximum time allowed for solve exceeded. |
| MinConNLP.WorkingSetSingularException |
Working set is singular in dual extended QP. |
| MinUnconMultiVar.ApproximateMinimumException |
Scaled step tolerance satisfied; the current point may be an approximate
local solution, or the algorithm is making very slow progress and is not
near a solution, or the scaled step tolerance is too big. |
| MinUnconMultiVar.FalseConvergenceException |
False convergence error; the iterates appear to be converging to a noncritical
point. |
| MinUnconMultiVar.MaxIterationsException |
Maximum number of iterations exceeded. |
| MinUnconMultiVar.UnboundedBelowException |
Five consecutive steps of the maximum allowable stepsize have been taken, either the
function is unbounded below, or has a finite asymptote in some direction
or the maximum allowable step size is too small. |
| NonlinLeastSquares.NoProgressException |
The algorithm is not making any progress, try new initial guess. |
| NonlinLeastSquares.TooManyIterationsException |
Too many iterations. |
| NonNegativeLeastSquares.TooManyIterException |
Maximum number of iterations has been exceeded. |
| NonNegativeLeastSquares.TooMuchTimeException |
Maximum time allowed for solve is exceeded. |
| OdeAdamsGear.DidNotConvergeException |
The iteration did not converge within the maximum number of steps allowed (default 500). |
| OdeAdamsGear.MaxFcnEvalsExceededException |
Maximum function evaluations exceeded. |
| OdeAdamsGear.SingularMatrixException |
The interpolation matrix is singular. |
| OdeAdamsGear.ToleranceTooSmallException |
Tolerance is too small or the problem is stiff. |
| OdeRungeKutta.DidNotConvergeException |
The iteration did not converge within the maximum number of steps allowed (default 500). |
| OdeRungeKutta.ToleranceTooSmallException |
Tolerance is too small or the problem is stiff. |
| QuadraticProgramming.InconsistentSystemException |
The system of constraints is inconsistent. |
| QuadraticProgramming.NoLPSolutionException |
No solution for the LP problem with h = 0 was found by DenseLP. |
| QuadraticProgramming.ProblemUnboundedException |
The object value for the problem is unbounded. |
| QuadraticProgramming.SolutionNotFoundException |
A solution was not found. |
| SingularMatrixException |
The matrix is singular. |
| SparseCholesky.NotSPDException |
The matrix is not symmetric, positive definite. |
| SVD.DidNotConvergeException |
The iteration did not converge |
| ZeroPolynomial.DidNotConvergeException |
The iteration did not converge |
| ZeroSystem.DidNotConvergeException |
The iteration did not converge. |
| ZeroSystem.ToleranceTooSmallException |
Tolerance too small |
| ZeroSystem.TooManyIterationsException |
Too many iterations. |