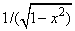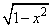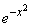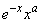Usage Notes
Univariate Quadrature
The first nine functions in this chapter section are designed to compute approximations to integrals of the form
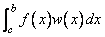
The weight function w is used to incorporate known singularities (either algebraic or logarithmic) or to incorporate oscillations. For general-purpose integration, we recommend the use of imsl_f_int_fcn_sing (even if no endpoint singularities are present). If more efficiency is desired, then the use of one of the more specialized functions should be considered. These functions are organized as follows:
• w = 1
imsl_f_int_fcn_sing
imsl_f_int_fcn
imsl_f_int_fcn_sing_pts
imsl_f_int_fcn_inf
imsl_f_int_fcn_smooth
• w(x) = sinωx or w(x) = cosωx
imsl_f_int_fcn_trig (for a finite interval)
imsl_f_int_fcn_fourier (for an infinite interval)
• w(x) = (x − a)a(b − x)bln(x − a)ln(b − x) where the ln factors are optional
imsl_f_int_fcn_alg_log
• w(x) = 1/(x − c)
imsl_f_int_fcn_cauchy
The calling sequences for these functions are very similar. The function to be integrated is always fcn, and the lower and upper limits are a and b, respectively. The requested absolute error ɛ is err_abs, while the requested relative error ρ is err_rel. These quadrature functions return the estimated answer R. An optional value err_est = E estimates the error. These numbers are related as follows:
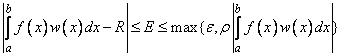
Several of the univariate quadrature functions have arguments of type imsl_quad, which is defined in imsl.h.
One situation that occasionally arises in univariate quadrature concerns the approximation of integrals when only tabular data are given. The functions described above do not directly address this question. However, the standard method for handling this problem is first to interpolate the data, and then to integrate the interpolant. This can be accomplished by using the IMSL spline interpolation functions with one of the spline integration functions, which can be found in Chapter 3, “Interpolation and Approximation.”
Multivariate Quadrature
Two functions have been included in this chaptersection that are of use in approximating certain multivariate integrals. In particular, the function imsl_f_int_fcn_2d returns an approximation to an iterated two-dimensional integral of the form
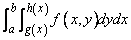
The second function, imsl_f_int_fcn_hpyer_rect, returns an approximation to the integral of a function of n variables over a hyper-rectangle
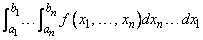
When working with two-dimensional tensor-product tabular
data, use the IMSL
spline interpolation function imsl_f_spline_2d_interp,
followed by the IMSL spline integration function imsl_f_spline_2d_integral described in
Chapter 3, “Interpolation and
Approximation”.
Gauss Quadrature
Before computing Gauss quadratures, you must compute so-called Gauss quadrature rules that integrate polynomials of as high degree as possible. These quadrature rules can be easily computed using the function imsl_f_gauss_quad_rule, which produces the points {wi} for i = 1, ¼, N that satisfy
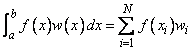
for all functions f that are polynomials of degree less than 2N. The weight functions w may be selected from the following table.
|
w(x) |
Interval |
Name |
|
1 |
(-1, 1) |
Legendre |
|
|
(-1, 1) |
Chebyshev 1st kind |
|
|
(-1, 1) |
Chebyshev 2nd kind |
|
|
(-¥, ¥) |
Hermite |
|
(1 + x)a (1 - x)b |
(-1, 1) |
Jacobi |
|
|
(0, ¥) |
Generalized Laguerre |
|
1/cosh (x) |
(-¥, ¥) |
Hyperbolic cosine |
Where permissible, imsl_f_gauss_quad_rule also computes Gauss-Radau and Gauss-Lobatto quadrature rules.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |