InvCdf.Chi Method

InvCdfChi Method

Evaluates the inverse of the chi-squared cumulative probability distribution function.

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

public static double Chi(
	double p,
	double df
)

Public Shared Function Chi ( 
	p As Double,
	df As Double
) As Double

public:
static double Chi(
	double p, 
	double df
)

static member Chi : 
        p : float * 
        df : float -> float

Parameters

p: Type: SystemDouble
A double scalar value representing the probability for which the inverse chi-squared function is to be evaluated.
df: Type: SystemDouble
A double scalar value representing the number of degrees of freedom. This must be at least 0.5.

Return Value

Type: Double
A double scalar value. The probability that a chi-squared random variable takes a value less than or equal to this returned value is p.

Remarks

Method InvCdf.Chi evaluates the inverse distribution function of a chi-squared random variable with df degrees of freedom, that is, with P = p and v = df, it determines x (equal to InvCdf.Chi(p, df)), such that

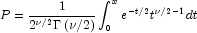$P=\frac{1}{{2^{\nu/2}\Gamma\left({\nu/2} \right)}}\int_0^x{e^{-t/2}t^{\nu/2-1}}dt$

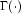where $\Gamma(\cdot)$ is the Gamma function. The probability that the random variable takes a value less than or equal to x is P.

For $v\lt 40$ , InvCdf.Chi uses bisection, if $v\ge 2$ or $P\gt 0.98$ , or regula falsi to find the point at which the chi-squared distribution function is equal to P. The distribution function is evaluated using Cdf.Chi.

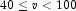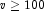For $40\le v\lt 100$ , a modified Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.18) to the normal distribution is used, and InvCdf.Normal is used to evaluate the inverse of the normal distribution function. For $v\ge 100$ , the ordinary Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) is used.

Reference

InvCdf Class

Imsl.Stat Namespace

Other Resources

Example