| InvCdfNoncentralF Method |
Evaluates the inverse of the noncentral F cumulative distribution
function (CDF).
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
Parameters
- p
- Type: SystemDouble
A double scalar value representing the probability for which the inverse of the noncentral F cumulative distribution function is to be evaluated. p must be non-negative and less than one. - dfn
- Type: SystemDouble
A double scalar value representing the number of numerator degrees of freedom. dfn must be positive. - dfd
- Type: SystemDouble
A double scalar value representing the number of denominator degrees of freedom. dfd must be positive. - lambda
- Type: SystemDouble
A double scalar value representing the noncentrality parameter. lambda must nonnegative.
Return Value
Type: DoubleA double scalar value representing the inverse of the noncentral F distribution function evaluated at p. The probability that a noncentral F random variable takes a value less than or equal to InvCdf.NoncentralF(p, dfn, dfd, lambda) is p.
If 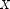 is a noncentral chi-square random
variable with noncentrality parameter
is a noncentral chi-square random
variable with noncentrality parameter  and
and 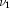 degrees of freedom, and
degrees of freedom, and  is a chi-square random variable with
is a chi-square random variable with  degrees of freedom which is statistically independent
of
degrees of freedom which is statistically independent
of 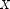 , then
, then
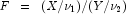 is a noncentral F-distributed random variable whose CDF is
given by:
is a noncentral F-distributed random variable whose CDF is
given by:
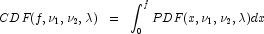 where the probability density function
where the probability density function 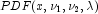 is given by:
is given by:
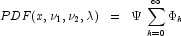
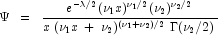
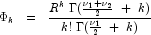
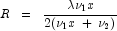 where
where 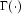 is the Gamma
function,
is the Gamma
function, 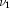 = dfn,
= dfn,  = dfd,
= dfd,  =
lambda, and
=
lambda, and 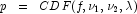 is the probability that
is the probability that 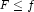 .
.
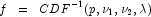 Method InvCdf.NoncentralF uses bisection and modified regula
falsi search algorithms to invert the distribution function
Method InvCdf.NoncentralF uses bisection and modified regula
falsi search algorithms to invert the distribution function
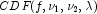 , which is evaluated
using method Cdf.NoncentralF. For sufficiently small
p, an accurate approximation of
, which is evaluated
using method Cdf.NoncentralF. For sufficiently small
p, an accurate approximation of 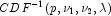 can be used which requires no such
inverse search algorithms.
can be used which requires no such
inverse search algorithms.
Method InvCdf.NoncentralF evaluates