Click or drag to resize
InvCdfNoncentralchi Method
Evaluates the inverse of the noncentral chi-squared cumulative probability distribution function.

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
Syntax
Copy
public static double Noncentralchi(
	double p,
	double df,
	double alam
)

Parameters

p
Type: SystemDouble
A double scalar value representing the probability for which the inverse noncentral chi-squared distribution function is to be evaluated. p must be in the open interval (0.0, 1.0).
df
Type: SystemDouble
A double scalar value representing the number of degrees of freedom. This must be at least 0.5. but less than or equal to 200,000.
alam
Type: SystemDouble
A double scalar value representing the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.

Return Value

Type: Double
A double scalar value. The probability that a noncentral chi-squared random variable takes a value less than or equal to this returned value is p.
Remarks
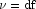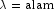Method InvCdf.Noncentralchi evaluates the inverse distribution function of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with P =p, \nu={\rm df}, and \lambda={\rm alam}, it determines 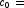c_{0}=InvCdf.Noncentralchi(p, df, alam), such that
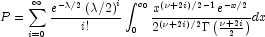P=\sum\limits_{i=0}^\infty{\frac{e^{ -\lambda/2}\left(\lambda/2\right)^i}{i!}}\int_0^{c_{0}}{\frac{x^{ \left(\nu+2i\right)/2-1}e^{-x/2}}{2^{\left(\nu+2i\right)/2}{\Gamma \left(\frac{\nu+2i}{2}\right)}}}dx
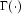where \Gamma(\cdot) is the Gamma function. The probability that the random variable takes a value less than or equal to c_{0} is P.

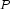Method InvCdf.Noncentralchi uses bisection and modified regula falsi to invert the distribution function, which is evaluated using Cdf.Noncentralchi. See Cdf.Noncentralchi for an alternative definition of the noncentral chi-squared random variable in terms of normal random variables.

See Also