InvCdf.NoncentralBeta Method

InvCdfNoncentralBeta Method

Evaluates the inverse of the noncentral beta cumulative distribution function (CDF).

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

public static double NoncentralBeta(
	double p,
	double shape1,
	double shape2,
	double lambda
)

Public Shared Function NoncentralBeta ( 
	p As Double,
	shape1 As Double,
	shape2 As Double,
	lambda As Double
) As Double

public:
static double NoncentralBeta(
	double p, 
	double shape1, 
	double shape2, 
	double lambda
)

static member NoncentralBeta : 
        p : float * 
        shape1 : float * 
        shape2 : float * 
        lambda : float -> float

Parameters

p: Type: SystemDouble
A double scalar value representing the probability for which the inverse of the noncentral beta cumulative distribution function is to be evaluated. p must be non-negative and less than or equal to one.
shape1: Type: SystemDouble
A double scalar value representing the first shape parameter. shape1 must be positive.
shape2: Type: SystemDouble
A double scalar value representing the second shape parameter. shape2 must be positive.
lambda: Type: SystemDouble
A double scalar value representing the noncentrality parameter. lambda must be nonnegative.

Return Value

Type: Double
A double scalar value representing the inverse of the noncentral beta distribution function evaluated at p. The probability that a noncentral beta random variable takes a value less than or equal to NoncentralBeta is p.

Remarks

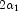is a noncentral chi-square random variable with noncentrality parameter $\lambda$ and $2\alpha_1$ degrees of freedom, and

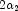is a chi-square random variable with $2\alpha_2$ degrees of freedom which is statistically independent of

, then

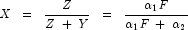$X\;\;=\;\;\frac{Z}{Z\;+\;Y}\;\;=\;\; \frac{\alpha_1 F}{\alpha_1 F\;+\;\alpha_2}$

is a noncentral beta-distributed random variable and

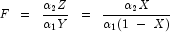$F\;\;=\;\;\frac{\alpha_2 Z}{\alpha_1 Y}\; \;=\;\;\frac{\alpha_2 X}{\alpha_1(1\;-\;X)}$

is a noncentral F-distributed random variable. The CDF for noncentral beta variable X can thus be simply defined in terms of the noncentral F CDF:

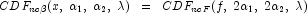$CDF_{nc\beta}(x,\;\alpha_1,\;\alpha_2,\; \lambda)\;\;=\;\;CDF_{ncF}(f,\;2\alpha_1,\;2\alpha_2,\;\lambda)$

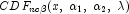where $CDF_{nc\beta}(x,\;\alpha_1,\;\alpha_2,\;\lambda)$ is the noncentral beta CDF with

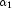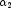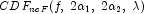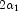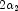= x, $\alpha_1$ = shape1, $\alpha_2$ = shape2, and noncentrality parameter $\lambda$ = lambda; $CDF_{ncF} (f,\;2\alpha_1,\;2\alpha_2,\;\lambda)$ is the noncentral F CDF with argument f, numerator and denominator degrees of freedom $2\alpha_1$ and $2\alpha_2$ respectively, and noncentrality parameter $\lambda$ ; and:

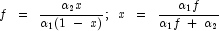$f\;\;=\;\;\frac{\alpha_2 x}{\alpha_1(1\;- \;x)};\;\;x\;\;=\;\;\frac{\alpha_1 f}{\alpha_1 f\;+\;\alpha_2}$

(See documentation for class Cdf method NoncentralF for a discussion of how the noncentral F CDF is defined and calculated.)

Method InvCdf.NoncentralBeta evaluates

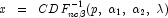$x\;\;=\;\;CDF_{nc\beta}^{-1}(p,\; \alpha_1,\;\alpha_2,\;\lambda)$

by first evaluating:

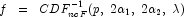$f\;\;=\;\;CDF_{ncF}^{-1}(p,\;2\alpha_1,\; 2\alpha_2,\;\lambda)$

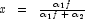and then solving for x using $x\;\;=\;\;\frac{ \alpha_1 f}{\alpha_1 f\;+\;\alpha_2}$ . (See documentation for InvCdf.NoncentralF for a discussion of how the inverse noncentral F CDF is calculated.)

Reference

InvCdf Class

Imsl.Stat Namespace