Usage Notes
The majority of the functions in this chaptersection produce cubic piecewise polynomial or general spline functions that either interpolate or approximate given data or support the evaluation and integration of these functions. Two major subdivisions of functions are provided. The cubic spline functions begin with the prefix “cub_spline_” and use the piecewise polynomial representation described below. The spline functions begin with the prefix “spline_” and use the B-spline representation described below. Most of the spline functions are based on routines in the book by de Boor (1978).
We provide a few general purpose routines for general least-squares fit to data and a routine that produces an interpolant to two-dimensional scattered data.
Piecewise Polynomials
A univariate piecewise polynomial (function) p is specified by giving its breakpoint sequence ξ Î Rn, the order k (degree k − 1) of its polynomial pieces, and the k ´ (n - 1) matrix c of its local polynomial coefficients. In terms of this information, the piecewise polynomial (ppoly) function is given by
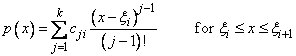
The breakpoint sequence ξ is assumed to be strictly increasing, and we extend the ppoly function to the entire real axis by extrapolation from the first and last intervals. This representation is redundant when the ppoly function is known to be smooth. For example, if p is known to be continuous, then we can compute c1,i+1 from the cii as follows:
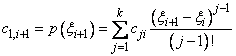
For smooth ppoly, we prefer to use the nonredundant representation in terms of the “basis” or B-splines, at least when such a function is first to be determined.
Splines and B-Splines
B-splines provide a particularly
convenient and suitable basis for a given class of smooth ppoly functions. Such
a class is specified by giving its breakpoint sequence, its order k, and
the required smoothness across each of the interior breakpoints. The
corresponding B-spline basis is specified by giving its knot sequence
t Î RM. The
specification rule is as follows: If the class is to have all derivatives up to
and including the j-th derivative continuous across the interior
breakpoint ξi, then the number
ξi should occur
k − j - 1 times in the knot sequence. Assuming
that ξ1 and ξn are the endpoints of the interval of
interest, choose the first k knots equal to ξ1 and the last
k knots equal to ξn. This can be done because the B-splines
are defined to be right continuous near ξ1 and left
continuous near ξn.
When the above construction is completed, a knot sequence t of length M is generated, and there are m: = M - k B-splines of order k, for exampleB0, ¼, Bm-1, spanning the ppoly functions on the interval with the indicated smoothness. That is, each ppoly function in this class has a unique representation
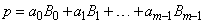
as a linear combination of B-splines. A B-spline is a particularly compact ppoly function. Bi is a nonnegative function that is nonzero only on the interval [ti,ti+k]. More precisely, the support of the i-th B-spline is [ti,ti+k]. No ppoly function in the same class (other than the zero function) has smaller support (i.e., vanishes on more intervals) than a B-spline. This makes B-splines particularly attractive basis functions since the influence of any particular B-spline coefficient extends only over a few intervals. When it is necessary to emphasize the dependence of the B-spline on its parameters, we will use the notation Bi,k,t to denote the i-th B-spline of order k for the knot sequence t.
Cubic Splines
Cubic splines are smooth (i.e., C1 or C2), fourth-order ppoly functions. For historical and other reasons, cubic splines are the most heavily used ppoly functions. Therefore, we provide special functions for their construction and evaluation. These routines use the ppoly representation as described above for general ppoly functions (with k = 4).
We provide two cubic spline interpolation functions: imsl_f_cub_spline_interp_e_cnd and imsl_f_cub_spline_interp_shape. The function imsl_f_cub_spline_interp_e_cnd allows the user to specify various endpoint conditions (such as the value of the first or second derivative at the right and left points). This means that the natural cubic spline can be obtained using this function by setting the second derivative to zero at both endpoints. The function imsl_f_cub_spline_interp_shape is designed so that the shape of the curve matches the shape of the data. In particular, one option of this function preserves the convexity of the data while the default attempts to minimize oscillations.
It is possible that the cubic spline interpolation functions will produce unsatisfactory results. For example, the interpolant may not have the shape required by the user, or the data may be noisy and require a least-squares fit. The interpolation function imsl_f_spline_interp is more flexible, as it allows you to choose the knots and order of the spline interpolant. We encourage the user to use this routine and exploit the flexibility provided.
Tensor Product Splines
The simplest method of obtaining multivariate interpolation and approximation functions is to take univariate methods and form a multivariate method via tensor products. In the case of two-dimensional spline interpolation, the derivation proceeds as follows. Let tx be a knot sequence for splines of order kx, and tv be a knot sequence for splines of order kv. Let Nx + kx be the length of tx, and Nv + kx be the length of tv. Then, the tensor-product spline has the following form.
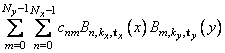
Given two sets of points
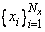
and
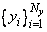
for which the corresponding univariate interpolation problem can be solved, the tensor-product interpolation problem finds the coefficients cnm so that
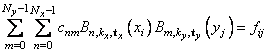
This problem can be solved efficiently by repeatedly solving univariate interpolation problems as described in de Boor (1978, p. 347). Three-dimensional interpolation can be handled in an analogous manner. This chaptersection provides functions that compute the two-dimensional, tensor-product spline coefficients given two-dimensional interpolation data (imsl_f_spline_2d_interp) and that compute the two-dimensional, tensor-product spline coefficients for a tensor-product, least-squares problem (imsl_f_spline_2d_least_squares). In addition, we provide evaluation, differentiation, and integration functions for the two-dimensional, tensor-product spline functions. The relevant functions are imsl_f_spline_2d_value and imsl_f_spline_2d_integral.
Scattered Data Interpolation
The IMSL C/Math/Library provides one function, imsl_f_scattered_2d_interp, that returns values of an interpolant to scattered data in the plane. This function is based on work by Akima (1978), which uses C1 piecewise quintics on a triangular mesh.
Least Squares
The IMSL C/Math/Library includes functions for smoothing noisy data. The function imsl_f_user_fcn_least_squares computes regressions with user-supplied functions. The function imsl_f_spline_least_squares computes a least-squares fit using splines with fixed knots or variable knots. These functions produce cubic spline, least-squares fit by default. Optional arguments allow the user to choose the order and the knot sequence. IMSL C/Math/Library also includes a tensor-product spline regression function (imsl_f_spline_2d_least_squares), mentioned above. The function imsl_f_radial_scattered_fit computes an approximation to scattered data in RN using radial-basis functions.
In addition to the functions listed above, several functions in Chapter 10, “Statistics and Random Number Generation”, provide for polynomial regression and general linear regression.
Smoothing by Cubic Splines
One ‘‘smoothing spline’’ function is provided. The default action of imsl_f_cub_spline_smooth estimates a smoothing parameter by cross-validation and then returns the cubic spline that smooths the data. If the user wishes to supply a smoothing parameter, then this function returns the appropriate cubic spline.
Structures for Splines and Piecewise Polynomials
This optional section includes more details concerning the structures for splines and piecewise polynomials.
A spline may be viewed as a mapping with domain Rd and target Rr, where d and r are positive integers. For this version of the IMSL C/Math/Library, only r = 1 is supported. Thus, if s is a spline, then for some d and r
s : Rd ® Rr
This implies that such a spline s must have d knot sequences and orders (one for each domain dimension). Thus, associated with s, we have knots and orders
t0, ¼, td-1
k0, ¼, kd-1
The precise form of the spline follows:
s(x) = (s0(x), ¼, sr-1(x)) x = (x1, ¼, xd) Î Rd
where the following equation is true.
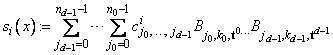
Note that ni is the number of knots in ti minus the order ki.
We store all the information for a spline in one structure called Imsl_f_spline. (If the type is double, then the structure name is Imsl_d_spline, and the float becomes double.) The specification for this structure follows:
typedef struct {
int domain_dim;
int target_dim;
int *order;
int *num_coef;
int *num_knots;
float **knots;
float **coef;
} Imsl_f_spline;
Explicitly, if sp is a pointer to Imsl_f_spline, then
|
sp-> domain_dim |
= d |
|
sp-> target_dim |
= r |
|
sp-> order [i] |
= ki i = 0, …, d - 1 |
|
sp-> num_coef [i] |
= mi i = 0, …, d - 1 |
|
sp-> num_knots [i] |
= ni + ki i = 0, …, d - 1 |
|
sp-> knots [i] [j] |
|
|
sp-> coef [i] [j] |
|
For ppoly functions, we
view a ppoly as
a mapping with domain Rd and target
Rr where d
and r are positive integers. Thus, if p is a ppoly, then for some
d and r the following is true.
p : Rd ® Rr
For this version of the C/Math/Library, only r = 1 is supported. This implies that such a ppoly p must have d breakpoint sequences and orders (one for each domain dimension). Thus, associated with p, we have breakpoints and orders
x1, …, xd
k1, …, kd
The precise form of the ppoly follows:
p(x) = (p0x), …, prx)) x = (x1, …, xd) Î Rd
where
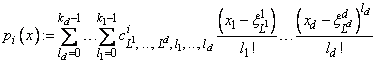
with
Lj : = max {1, min {Mj, nj - 1}}
where MJ is chosen so that
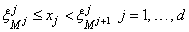
with
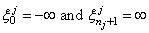
Note that ni is the number of breakpoints in ξj.
We store all the information for a ppoly in one structure called Imsl_f_ppoly. (If the type is double, then the structure name is Imsl_d_ppoly, and the float becomes double.) The following is the specification for this structure.
typedef struct {
int domain_dim;
int target_dim;
int *order;
int *num_coef;
int *num_breakpoints;
float **breakpoints;
float **coef;
} Imsl_f_ppoly;
In particular, if ppoly is a pointer to the structure of type Imsl_f_ppoly, then
|
ppoly-> domain_dim |
= d |
|
ppoly-> target_dim |
= r |
|
ppoly-> order [i] |
= ki i = 0, ¼, d - 1 |
|
ppoly-> num_coef [i] |
= ki (ni - 1) i = 0, ¼, d - 1 |
|
ppoly-> num_breakpoints [i] |
= ni i = 0, ¼, d - 1 |
|
ppoly-> breakpoints [i] [j] |
|
|
ppoly->coef [i[ [j] |
|
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |
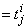 I
I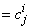 I
I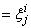 i = 0,
i = 0, 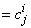 i
i