Routines
[A] [B] [C] [D] [E] [F] [G] [H] [ I ] [J] [K] [L] [M]
[N] [O] [P] [Q] [R] [S] [T] [U] [V] [W] [X] [Y] [Z]
Function Purpose Statement
A
C
|
Adds a scalar to each component of a vector, x ¬ x + a, all complex. | |
|
Computes the scalar times a vector plus a vector, y ¬ ax + y, all complex. | |
|
Copies a complex band matrix stored in complex band storage mode. | |
|
Converts a complex matrix in band storage mode to a complex matrix in full storage mode. | |
|
Converts a complex general matrix to a matrix in complex band storage mode. | |
|
Copies a complex general matrix. | |
|
Computes the convolution of two complex vectors. | |
|
Copies a vector x to a vector y, both complex. | |
|
Computes the correlation of two complex vectors. | |
|
Approximates the gradient using central differences. | |
|
Computes the complex conjugate dot product, | |
|
Computes the complex dot product xTy. | |
|
Computes one of the matrix-vector
operations: | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes one of the matrix-vector
operations: | |
|
Computes the rank-one update of a complex general
matrix: | |
|
Computes the rank-one update of a complex general
matrix: | |
|
Copies a complex Hermitian band matrix stored in band Hermitian storage mode to a complex band matrix stored in band storage mode. | |
|
Computes the matrix-vector operation | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes the matrix-vector operation | |
|
Computes the rank-one update of an Hermitian
matrix: | |
|
Computes a rank-two update of an Hermitian
matrix: | |
|
Computes one of the Hermitian rank 2k
operations: | |
|
Computes one of the Hermitian rank k
operations: | |
|
Extends a complex Hermitian matrix defined in its upper triangle to its lower triangle. | |
|
Checks a user-supplied gradient of a function. | |
|
Checks a user-supplied Hessian of an analytic function. | |
|
Checks a user-supplied Hessian of an analytic function. | |
|
Checks a user-supplied Jacobian of a system of equations with M functions in N unknowns. | |
|
Computes the condition number of a matrix. | |
|
Computes the condition number of a rectangular
| |
|
Computes the least-squares constrained spline approximation, returning the B-spline coefficients. | |
|
Returns the value of various mathematical and physical constants. | |
|
Returns CPU time used in seconds. | |
|
Converts a real matrix in band storage mode to a complex matrix in band storage mode. | |
|
Copies a real band matrix stored in band storage mode. | |
|
Converts a real matrix in band storage mode to a real general matrix. | |
|
Copies a real general matrix to a complex general matrix. | |
|
Converts a real general matrix to a matrix in band storage mode. | |
|
Copies a real general matrix. | |
|
Copies a real rectangular matrix to a complex rectangular matrix. | |
|
Evaluates the derivative of a cubic spline on a grid. | |
|
Computes the Akima cubic spline interpolant. | |
|
Copies a real symmetric band matrix stored in band symmetric storage mode to a real band matrix stored in band storage mode. | |
|
Multiplies a vector by a scalar, y ¬ ay, both complex. | |
|
Computes a cubic spline interpolant that is consistent with the concavity of the data. | |
|
Computes the cubic spline interpolant with specified derivative endpoint conditions. | |
|
Evaluates the derivative of a cubic spline. | |
|
Sets the components of a vector to a scalar, all complex. | |
|
Extends a real symmetric matrix defined in its upper triangle to its lower triangle. | |
|
Computes the cubic spline interpolant with the ‘not-a-knot' condition and return values of the interpolant at specified points. | |
|
Computes the cubic spline interpolant with the ‘not-a-knot' condition. | |
|
Evaluates the integral of a cubic spline. | |
|
Computes the cubic spline interpolant with periodic boundary conditions. | |
|
Applies a complex Givens plane rotation. | |
|
Applies a complex modified Givens plane rotation. | |
|
Multiplies a complex vector by a single-precision scalar, y ¬ ay. | |
|
Computes a smooth cubic spline approximation to noisy data using cross-validation to estimate the smoothing parameter. | |
|
Smooths one-dimensional data by error detection. | |
|
Computes a smooth cubic spline approximation to noisy data. | |
|
Subtracts each component of a vector from a scalar,
| |
|
Evaluates a cubic spline. | |
|
Multiplies a complex vector by a single-precision scalar and store the result in another complex vector, y ¬ ax. | |
|
Interchanges vectors x and y, both complex. | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes one of the symmetric rank 2k
operations: | |
|
Computes one of the symmetric rank k
operations: | |
|
Computes one of the matrix-vector
operations: | |
|
Solves one of the complex triangular systems: | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes one of the matrix-vector operations: | |
|
Solves one of the complex matrix equations: | |
|
Solves one of the complex
triangular systems: | |
|
Converts X in units XUNITS to Y in units YUNITS. | |
|
Multiplies a vector by a scalar and store the result in another vector, y ¬ ax, all complex. | |
|
Converts a character string containing an integer number into the corresponding integer form. | |
|
Computes the sum of a complex scalar plus a complex
conjugate dot product, | |
|
Computes the sum of a complex scalar, a complex dot product and the double-complex accumulator, which is set to the result ACC ¬ ACC + a + xTy. | |
|
Computes the complex conjugate dot product, | |
|
Computes the sum of a complex scalar plus a complex dot product using a double-complex accumulator, which is set to the result ACC ¬ a + xTy. | |
|
Computes the complex dot product xTy using a double-precision accumulator. | |
|
Computes the sum of a complex scalar plus a complex dot product, a + xTy, using a double-precision accumulator. |
D
|
Solves a first order differential-algebraic system of equations, g(t, y, y¢) = 0, using Petzold−Gear BDF method. | |
|
Solves a linear programming problem. | |
|
Computes the first, second or third derivative of a user-supplied function. | |
|
Computes the determinant of a rectangular matrix, A. | |
|
Constructs a square diagonal matrix from a rank-1 array or several diagonal matrices from a rank-2 array. | |
|
Extracts a rank-1 array whose values are the diagonal terms of a rank-2 array argument. | |
|
Computes the 1-norm distance between two points. | |
|
Computes the Euclidean (2-norm) distance between two points. | |
|
Computes the infinity norm distance between two points. | |
|
Solves a linear programming problem via the revised simplex algorithm. | |
|
See AMACH. | |
|
Adds a double-precision scalar to the accumulator in extended precision. | |
|
Initializes an extended-precision accumulator with a double-precision scalar. | |
|
Multiplies double-precision scalars in extended precision. | |
|
Stores a double-precision approximation to an extended-precision scalar. | |
|
Computes the single-precision dot product xTy using a double precision accumulator. This routine handles MATH/LIBRARY and STAT/LIBRARY type DOUBLE PRECISION options. | |
|
This routine handles MATH/LIBRARY and STAT/LIBRARY type DOUBLE PRECISION options. | |
|
|
|
E
|
Computes the eigenvalue-eigenvector decomposition of an ordinary or generalized eigenvalue problem. | |
|
Computes the performance index for a complex eigensystem. | |
|
Computes the performance index for a complex Hermitian eigensystem. | |
|
Computes the performance index for a real eigensystem. | |
|
Computes the performance index for a real symmetric eigensystem in band symmetric storage mode. | |
|
Computes the performance index for a real symmetric eigensystem. | |
|
Prints error messages that are generated by IMSL routines using EPACK. | |
|
Sets error handler default print and stop actions. | |
|
Computes the largest or smallest eigenvalues of a complex Hermitian matrix. | |
|
Computes the largest or smallest eigenvalues of a real symmetric matrix in band symmetric storage mode. | |
|
Computes the largest or smallest eigenvalues of a real symmetric matrix. | |
|
Computes the eigenvalues in a given range of a complex Hermitian matrix. | |
|
Computes the eigenvalues in a given interval of a real symmetric matrix stored in band symmetric storage mode. | |
|
Computes selected eigenvalues of a real symmetric matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a complex matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a complex upper Hessenberg matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a complex Hermitian matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a real matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a real upper Hessenberg matrix. | |
|
Computes all of the eigenvalues and eigenvectors of a real symmetric matrix in band symmetric storage mode. | |
|
Computes all of the eigenvalues and eigenvectors of a real symmetric matrix. | |
|
Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a complex Hermitian matrix. | |
|
Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a real symmetric matrix in band symmetric storage mode. | |
|
Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a real symmetric matrix. | |
|
Computes the eigenvalues in a given range and the corresponding eigenvectors of a complex Hermitian matrix. | |
|
Computes the eigenvalues in a given interval and the corresponding eigenvectors of a real symmetric matrix stored in band symmetric storage mode. | |
|
Computes selected eigenvalues and eigenvectors of a real symmetric matrix. | |
|
Computes all of the eigenvalues of a complex matrix. | |
|
Computes all of the eigenvalues of a complex upper Hessenberg matrix. | |
|
Computes all of the eigenvalues of a complex Hermitian matrix. | |
|
Computes all of the eigenvalues of a real matrix. | |
|
Computes all of the eigenvalues of a real upper Hessenberg matrix. | |
|
Computes all of the eigenvalues of a real symmetric matrix in band symmetric storage mode. | |
|
Computes all of the eigenvalues of a real symmetric matrix. | |
|
Creates a rank-2 square array whose diagonals are all the value one. |
F
|
Frees the structure containing information about the Faure sequence. | |
|
Shuffled Faure sequence initialization. | |
|
Computes a shuffled Faure sequence. | |
|
Computes the Discrete Fourier Transform | |
|
Computes the Discrete Fourier Transform (2DFT) | |
|
Computes the Discrete Fourier Transform (2DFT) | |
|
Computes parameters needed by FCOST. | |
|
Computes the discrete Fourier cosine transformation of an even sequence. | |
|
Approximates the gradient using forward differences. | |
|
Approximates the Hessian using forward differences and function values. | |
|
Approximates the Jacobian of M functions in N unknowns using forward differences. | |
|
The Discrete Fourier Transform of a complex sequence and its inverse transform. | |
|
The Discrete Fourier Transform of several complex or real sequences. | |
|
Computes the inverse Fourier transform of a complex periodic two-dimensional array. | |
|
Computes Fourier coefficients of a complex periodic two-dimensional array. | |
|
Computes the inverse Fourier transform of a complex periodic three-dimensional array. | |
|
Computes Fourier coefficients of a complex periodic threedimensional array. | |
|
Computes the complex periodic sequence from its Fourier coefficients. | |
|
Computes the Fourier coefficients of a complex periodic sequence. | |
|
Computes parameters needed by FFTCF and FFTCB. | |
|
Computes the real periodic sequence from its Fourier coefficients. | |
|
Computes the Fourier coefficients of a real periodic sequence. | |
|
Computes parameters needed by FFTRF and FFTRB. | |
|
Computes a least-squares approximation with user-supplied basis functions. | |
|
Solves Poisson's or Helmholtz's equation on a two-dimensional rectangle using a fast Poisson solver based on the HODIE finite-difference scheme on a uni mesh. | |
|
Solves Poisson's or Helmholtz's equation on a three-dimensional box using a fast Poisson solver based on the HODIE finite-difference scheme on a uniform mesh. | |
|
Computes a Fejér quadrature rule with various classical weight functions. | |
|
Computes parameters needed by FSINT. | |
|
Computes the discrete Fourier sine transformation of an odd sequence. |
G
|
Approximates the Hessian using forward differences and a user-supplied gradient. | |
|
Generates points in an N-dimensional space. | |
|
Uses restarted GMRES with reverse communication to generate an approximate solution of Ax = b. | |
|
Computes the performance index for a generalized complex eigensystem Az = lBz. | |
|
Computes the performance index for a generalized real eigensystem Az = lBz. | |
|
Computes the performance index for a generalized real symmetric eigensystem problem. | |
|
Computes a Gauss, Gauss-Radau or Gauss-Lobatto quadrature rule given the recurrence coefficients for the monic polynomials orthogonal with respect to the weight function. | |
|
Computes a Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule with various classical weight functions. | |
|
Computes all of the eigenvalues and eigenvectors of a generalized complex eigensystem Az = lBz. | |
|
Computes all of the eigenvalues and eigenvectors of a generalized real eigensystem Az = lBz. | |
|
Computes all of the eigenvalues and eigenvectors of the generalized real symmetric eigenvalue problem Az = lBz, with B symmetric positive definite. | |
|
Computes all of the eigenvalues of a generalized complex eigensystem Az = lBz. | |
|
Computes all of the eigenvalues of a generalized real eigensystem Az = lBz. | |
|
Computes all of the eigenvalues of the generalized real symmetric eigenvalue problem Az = lBz, with B symmetric positive definite. |
H
|
Computes the Hadamard product of two real rectangular matrices. | |
|
Computes |
I
|
Returns the integer ASCII value of a character argument. | |
|
Adds a scalar to each component of a vector, x ¬ x + a, all integer. Finds the smallest index of the component of a complex vector having maximum magnitude. | |
|
Finds the smallest index of the component of a complex vector having minimum magnitude. | |
|
Returns the ASCII value of a character converted to uppercase. | |
|
Copies a vector x to a vector y, both integer. | |
|
Computes the day of the week for a given date. | |
|
Retrieves the code for an informational error. | |
|
The inverse of the Discrete Fourier Transform of a complex sequence. | |
|
The inverse of the Discrete Fourier Transform of a complex sequence. | |
|
The inverse Discrete Fourier Transform of several complex or real sequences. | |
|
Checks if a value is NaN (not a number). | |
|
Compares two character strings using the ASCII collating sequence but without regard to case. | |
|
Determines the position in a string at which a given character sequence begins without regard to case. | |
|
Finds the smallest index of the maximum component of a integer vector. | |
|
Finds the smallest index of the minimum of an integer vector. | |
|
Retrieves integer machine constants. | |
|
Computes the inverse Laplace transform of a complex function. | |
|
Finds the smallest index of the component of a single-precision vector having maximum absolute value. | |
|
Finds the smallest index of the component of a single-precision vector having minimum absolute value. | |
|
Sets the components of a vector to a scalar, all integer. | |
|
Finds the smallest index of the component of a single-precision vector having maximum value. | |
|
Finds the smallest index of the component of a single-precision vector having minimum value. | |
|
This is a generic logical function used to test scalars or arrays for occurrence of an IEEE 754 Standard format of floating point (ANSI/IEEE 1985) NaN, or not-a-number. | |
|
Searches a sorted integer vector for a given integer and return its index. | |
|
Subtracts each component of a vector from a scalar,
| |
|
Sums the values of an integer vector. | |
|
Interchanges vectors x and y, both integer. | |
|
Sets or retrieves MATH/LIBRARY integer options. | |
|
Solves an initial-value problem y¢ = f(t, y) for ordinary differential equations using Runge-Kutta pairs of various orders. | |
|
Solves an initial-value problem for ordinary differential equations using either Adams-Moulton's or Gear's BDF method. | |
|
Solves an initial-value problem for ordinary differential equations using the Runge-Kutta-Verner fifth-order and sixth-order method. |
J
|
Solves a real symmetric definite linear system using the Jacobi preconditioned conjugate gradient method with reverse communication. |
L
|
Computes the Cholesky decomposition of a symmetric positive semidefinite matrix with optional column pivoting. | |
|
Solves a linear least-squares problem with linear constraints. | |
|
Minimizes a general objective function subject to linear equality/inequality constraints. | |
|
Minimizes a general objective function subject to linear equality/inequality constraints. | |
|
Downdates the RTR Cholesky factorization of a real symmetric positive definite matrix after a rank-one matrix is removed | |
|
Computes the LU factorization of a complex matrix in band storage mode and estimate its L1condition number. | |
|
Computes the LU factorization of a complex general matrix and estimate its L1 condition number. | |
|
Estimates the condition number of a complex triangular matrix. | |
|
Computes the RH R factorization of a complex Hermitian positive definite matrix and estimate its L1 condition number. | |
|
Computes the RT R Cholesky factorization of a real symmetric positive definite matrix and estimate its L1condition number. | |
|
Computes the U DUH factorization of a complex Hermitian matrix and estimate its L1 condition number. | |
|
Computes the RH R factorization of a complex Hermitian positive definite matrix in band Hermitian storage mode and estimate its L1 condition number. | |
|
Computes the RT R Cholesky factorization of a real symmetric positive definite matrix in band symmetric storage mode and estimate its L1 condition number. | |
|
Computes the LU factorization of a real matrix in band storage mode and estimate its L1 condition number. | |
|
Computes the LU factorization of a real general matrix and estimate its L1 condition number. | |
|
Estimates the condition number of a real triangular matrix. | |
|
Computes the U DUT factorization of a real symmetric matrix and estimate its L1condition number. | |
|
Computes the determinant of a complex matrix given the LU factorization of the matrix in band storage mode. | |
|
Computes the determinant of a complex general matrix given the LU factorization of the matrix. | |
|
Computes the determinant of a complex triangular matrix. | |
|
Computes the determinant of a complex Hermitian positive definite matrix given the RH R Cholesky factorization of the matrix. | |
|
Computes the determinant of a real symmetric positive definite matrix given the RH R Cholesky factorization of the matrix. | |
|
Computes the determinant of a complex Hermitian matrix given the U DUH factorization of the matrix. | |
|
Computes the determinant of a complex Hermitian positive definite matrix given the RH R Cholesky factorization in band Hermitian storage mode. | |
|
Computes the determinant of a real symmetric positive definite matrix given the RT R Cholesky factorization of the band symmetric storage mode. | |
|
Computes the determinant of a real matrix in band storage mode given the LU factorization of the matrix. | |
|
Computes the determinant of a real general matrix given the LU factorization of the matrix. | |
|
Computes the determinant of a real triangular matrix. | |
|
Computes the determinant of a real symmetric matrix given the U DUT factorization of the matrix. | |
|
Uses iterative refinement to improve the solution of a complex system of linear equations in band storage mode. | |
|
Uses iterative refinement to improve the solution of a complex general system of linear equations. | |
|
Uses iterative refinement to improve the solution of a complex Hermitian positive definite system of linear equations. | |
|
Uses iterative refinement to improve the solution of a real symmetric positive definite system of linear equations. | |
|
Uses iterative refinement to improve the solution of a complex Hermitian system of linear equations. | |
|
Uses iterative refinement to improve the solution of a complex Hermitian positive definite system of linear equations in band Hermitian storage mode. | |
|
Uses iterative refinement to improve the solution of a real symmetric positive definite system of linear equations in band symmetric storage mode. | |
|
Uses iterative refinement to improve the solution of a real system of linear equations in band storage mode. | |
|
Uses iterative refinement to improve the solution of a real general system of linear equations. | |
|
Uses iterative refinement to improve the solution of a real symmetric system of linear equations. | |
|
Solves a complex system of linear equations given the LU factorization of the coefficient matrix in band storage mode. | |
|
Solves a complex general system of linear equations given the LU factorization of the coefficient matrix. | |
|
Solves a complex Hermitian positive definite system of linear equations given the RH R factorization of the coefficient matrix. | |
|
Solves a real symmetric positive definite system of linear equations given the RT R Choleksy factorization of the coefficient matrix. | |
|
Solves a complex Hermitian system of linear equations given the U DUH factorization of the coefficient matrix. | |
|
Solves a complex Hermitian positive definite system of linear equations given the factorization of the coefficient matrix in band Hermitian storage mode. | |
|
Solves a real symmetric positive definite system of linear equations given the factorization of the coefficient matrix in band symmetric storage mode. | |
|
Solves a real system of linear equations given the LU factorization of the coefficient matrix in band storage mode. | |
|
Solves a real general system of linear equations given the LU factorization of the coefficient matrix. | |
|
Solves a real symmetric system of linear equations given the U DUT factorization of the coefficient matrix. | |
|
Solves a real sparse symmetric positive definite system of linear equations, given the Cholesky factorization of the coefficient matrix. | |
|
Solves a sparse system of linear equations given the LU factorization of the coefficient matrix. | |
|
Solves a complex sparse Hermitian positive definite system of linear equations, given the Cholesky factorization of the coefficient matrix. | |
|
Solves a complex sparse system of linear equations given the LU factorization of the coefficient matrix. | |
|
Computes the LU factorization of a complex matrix in band storage mode. | |
|
Computes the LU factorization of a complex general matrix. | |
|
Computes the RH R factorization of a complex Hermitian positive definite matrix. | |
|
Computes the RT R Cholesky factorization of a real symmetric positive definite matrix. | |
|
Computes the U DUH factorization of a complex Hermitian matrix. | |
|
Computes the RH R factorization of a complex Hermitian positive definite matrix in band Hermitian storage mode. | |
|
Computes the RT R Cholesky factorization of a real symmetric positive definite matrix in band symmetric storage mode. | |
|
Computes the LU factorization of a real matrix in band storage mode. | |
|
Computes the LU factorization of a real general matrix. | |
|
Computes the U DUT factorization of a real symmetric matrix. | |
|
Computes the LU factorization of a real general sparse matrix. | |
|
Computes the LU factorization of a complex general sparse matrix. | |
|
Computes the inverse of a complex general matrix. | |
|
Computes the inverse of a complex triangular matrix. | |
|
Computes the inverse of a real symmetric positive definite matrix. | |
|
Computes the inverse of a real general matrix. | |
|
Computes the inverse of a real triangular matrix. | |
|
Computes the eigenvalues of a self-adjoint | |
|
Computes the eigenvalues of a self-adjoint | |
|
Computes the generalized eigenvalues of an n
´ n | |
|
Solves a general system of linear equations Ax = b. | |
|
Solves a rectangular system of linear equations
Ax @ b, | |
|
Solves a system of linear equations Ax = b, where A is a self-adjoint matrix. | |
|
Solves a rectangular least-squares system of linear equations Ax @ b using singular value decomposition. | |
|
Solves multiple systems of linear equations. | |
|
Computes the singular value decomposition (SVD) of a rectangular matrix, A. | |
|
Computes the numerical Cholesky factorization of a sparse symmetrical matrix A. | |
|
Computes the numerical Cholesky factorization of a sparse Hermitian matrix A. | |
|
Accumulates the orthogonal matrix Q from its factored form given the QR factorization of a rectangular matrix A. | |
|
Computes the QR decomposition, AP = QR, using Householder transformations. | |
|
Computes the least-squares solution using Householder transformations applied in blocked form. | |
|
Computes the coordinate transformation, projection, and complete the solution of the least-squares problem Ax = b. | |
|
Solves a complex system of linear equations in band storage mode with iterative refinement. | |
|
Solves a complex general system of linear equations with iterative refinement. | |
|
Solves a Hermitian positive definite system of linear equations with iterative refinement. | |
|
Solves a real symmetric positive definite system of linear equations with iterative refinement. | |
|
Solves a complex Hermitian system of linear equations with iterative refinement. | |
|
Solves a complex Hermitian positive definite system of linear equations in band Hermitian storage mode with iterative refinement. | |
|
Solves a real symmetric positive definite system of linear equations in band symmetric storage mode with iterative refinement. | |
|
Solves a real system of linear equations in band storage mode with iterative refinement. | |
|
Solves a real general system of linear equations with iterative refinement. | |
|
Solves a real symmetric system of linear equations with iterative refinement. | |
|
Solves a linear least-squares problem with iterative refinement. | |
|
Performs the symbolic Cholesky factorization for a sparse symmetric matrix using a minimum degree ordering or a userspecified ordering, and set up the data structure for the numerical Cholesky factorization. | |
|
Computes the generalized inverse of a real matrix. | |
|
Solves a complex system of linear equations in band storage mode without iterative refinement. | |
|
Solves a complex circulant linear system. | |
|
Solves a complex general system of linear equations without iterative refinement. | |
|
Computes the LDU factorization of a complex tridiagonal matrix A using a cyclic reduction algorithm. | |
|
Computes the LDU factorization of a real tridiagonal matrix A using a cyclic reduction algorithm. | |
|
Solves a complex triangular system of linear equations. | |
|
Solves a complex Hermitian positive definite system of linear equations without iterative refinement. | |
|
Solves a real symmetric positive definite system of linear equations without iterative refinement. | |
|
Solves a complex Hermitian system of linear equations without iterative refinement. | |
|
Computes the RT DR Cholesky factorization of a real symmetric positive definite matrix A in codiagonal band symmetric storage mode. Solve a system Ax = b. | |
|
Computes the RH DR Cholesky factorization of a complex hermitian positive-definite matrix A in codiagonal band hermitian storage mode. Solve a system Ax = b. | |
|
Solves a complex Hermitian positive definite system of linearequations in band Hermitian storage mode without iterative refinement. | |
|
Solves a real symmetric positive definite system of linear equations in band symmetric storage mode without iterative refinement. | |
|
Solves a real system of linear equations in band storage mode without iterative refinement. | |
|
Solves a real general system of linear equations without iterative refinement. | |
|
Solves a real triangular system of linear equations. | |
|
Solves a real symmetric system of linear equations without iterative refinement. | |
|
Solves a complex Toeplitz linear system. | |
|
Solves a real Toeplitz linear system. | |
|
Solves a complex tridiagonal system of linear equations. | |
|
Solves a real tridiagonal system of linear equations. | |
|
Solves a sparse system of symmetric positive definite linear algebraic equations by Gaussian elimination. | |
|
Solves a sparse system of linear algebraic equations by Gaussian elimination. | |
|
Solves a complex sparse Hermitian positive definite system of linear equations by Gaussian elimination. | |
|
Solves a complex sparse system of linear equations by Gaussian elimination. | |
|
Solves a linear least-squares problem without iterative refinement. | |
|
Computes the singular value decomposition of a complex matrix. | |
|
Computes the singular value decomposition of a real matrix. | |
|
Updates the RTR Cholesky factorization of a real symmetric positive definite matrix after a rank-one matrix is added. | |
|
Computes an updated QR factorization after the rank-one matrix axyT is added. |
M
|
Multiplies two complex rectangular matrices, AB. | |
|
Solves a system of partial differential equations of the form ut = f(x, t, u, ux, uxx) using the method of lines. The solution is represented with cubic Hermite polynomials. | |
|
Initializes or finalizes MPI. | |
|
Deallocates the space allocated for the IMSL derived type s_MPS. This routine is usually used in conjunction with READ_MPS. | |
|
Multiplies two real rectangular matrices, AB. | |
|
Multiplies a complex band matrix in band storage mode by a complex vector. | |
|
Multiplies a complex rectangular matrix by a complex vector. | |
|
Multiplies a real band matrix in band storage mode by a real vector. | |
|
Multiplies a real rectangular matrix by a vector. | |
|
Computes the transpose product of a matrix, ATA. | |
|
Multiplies the transpose of matrix A by matrix B, ATB. | |
|
Multiplies a matrx A by the transpose of a matrix B, ABT. |
N
|
Returns, as a scalar function, a value corresponding to the IEEE 754 Standard format of floating point (ANSI/IEEE 1985) for NaN. | |
|
Retrieves an error type for the most recently called IMSL routine. | |
|
Computes the number of days from January 1, 1900, to the given date. | |
|
Gives the date corresponding to the number of days since January 1, 1900. | |
|
Solves a system of nonlinear equations using factored secant update with a finite-difference approximation to the Jacobian. | |
|
Solves a system of nonlinear equations using factored secant update with a user-supplied Jacobian. | |
|
Solves a system of nonlinear equations using a modified Powell hybrid algorithm and a finite-difference approximation to the Jacobian. | |
|
Solves a system of nonlinear equations using a modified Powell hybrid algorithm with a user-supplied Jacobian. | |
|
Uses a sequential equality constrained QP method. | |
|
Uses a sequential equality constrained QP method. | |
|
Computes the norm of a rank-1 or rank-2 array. For rank-3 arrays, the norms of each rank-2 array, in dimension 3, are computed. | |
|
Computes the 1-norm of a complex band matrix in band storage mode. | |
|
Computes the 1-norm of a real band matrix in band storage mode. | |
|
Computes the 1-norm of a real matrix. | |
|
Computes the Frobenius norm of a real rectangular matrix. | |
|
Computes the infinity norm of a real matrix. |
O
|
OPERATORS: |
|
|
Computes transpose and conjugate transpose of a matrix. | |
|
Computes matrix-vector and matrix-matrix products. | |
|
Computes the inverse matrix, for square non-singular matrices. | |
|
Computes the inverse matrix times a vector or matrix for square non-singular matrices. | |
|
Computes transpose and conjugate transpose of a matrix. | |
|
Computes matrix-vector and matrix-matrix products. | |
|
Computes matrix-vector and matrix-matrix products. | |
|
Computes matrix-vector and matrix-matrix products. | |
|
Computes the inverse matrix times a vector or matrix for square non-singular matrices. | |
|
Computes matrix-vector and matrix-matrix products. | |
|
Orthogonalizes the columns of a rank-2 or rank-3 array. |
P
|
Solves a real symmetric definite linear system using a preconditioned conjugate gradient method with reverse communication. | |
|
Solves a linear, non-negative constrained least-squares
| |
|
Solves a linear least-squares system with bounds on
| |
|
Method of lines with Variable Griddings. | |
|
Permutes the rows or columns of a matrix. | |
|
Rearranges the elements of an array as specified by a permutation. | |
|
Prints a plot of up to 10 sets of points. | |
|
Prints a plot of up to 10 sets of points. | |
|
Evaluates a real general matrix polynomial. | |
|
Evaluates the derivative of a piecewise polynomial on a grid. | |
|
Evaluates the derivative of a piecewise polynomial. | |
|
Evaluates the integral of a piecewise polynomial. | |
|
Evaluates a piecewise polynomial. | |
|
Decomposes an integer into its prime factors. |
Q
|
Integrates a function on a hyper-rectangle. | |
|
Computes a sequence from its cosine Fourier coefficients with only odd wave numbers. | |
|
Computes the coefficients of the cosine Fourier transform with only odd wave numbers. | |
|
Computes parameters needed by QCOSF and QCOSB. | |
|
Evaluates the derivative of a function defined on a rectangular grid using quadratic interpolation. | |
|
Evaluates a function defined on a rectangular grid using quadratic interpolation. | |
|
Evaluates the derivative of a function defined on a rectangular three-dimensional grid using quadratic interpolation. | |
|
Evaluates a function defined on a rectangular three-dimensional grid using quadratic interpolation. | |
|
Integrates a function using a globally adaptive scheme based on Gauss-Kronrod rules. | |
|
Integrates a function over an infinite or semi-infinite interval. | |
|
Integrates a function with singularity points given. | |
|
Integrates a function (which may have endpoint singularities). | |
|
Integrates a function F(X)/(X - C) in the Cauchy principal value sense. | |
|
Computes a Fourier integral. | |
|
Integrates a function containing a sine or a cosine. | |
|
Integrates a function with algebraic-logarithmic singularities. | |
|
Evaluates the derivative of a function defined on a set of points using quadratic interpolation. | |
|
Integrates a smooth function using a nonadaptive rule. | |
|
Evaluates a function defined on a set of points using quadratic interpolation. | |
|
Integrates a function over a hyperrectangle using a
| |
|
Solves a quadratic programming problem subject to linear equality/inequality constraints. | |
|
Computes a sequence from its sine Fourier coefficients with only odd wave numbers. | |
|
Computes the coefficients of the sine Fourier transform with only odd wave numbers. | |
|
Computes parameters needed by QSINF and QSINB. |
R
|
Computes a scalar, rank-1, rank-2 or rank-3 array of random numbers. | |
|
Generates a rank-1 array of random numbers. | |
|
Computes the mathematical rank of a rank-2 or rank-3 array. | |
|
Computes a rational weighted Chebyshev approximation to a continuous function on an interval. | |
|
Computes the convolution of two real vectors. | |
|
Computes the correlation of two real vectors. | |
|
Fits a polynomial curve using least squares. | |
|
Reads an MPS file containing a linear program problem or a quadratic programming problem. | |
|
Computes recurrence coefficients for various monic polynomials. | |
|
Computes recurrence coefficients for monic polynomials given a quadrature rule. | |
|
Fits a line to a set of data points using least squares. | |
|
Retrieves the current value of the seed used in the IMSL random number generators. | |
|
Initializes the 32-bit Merseene Twister generator using an array. | |
|
Retrieves the current table used in the 32-bit
| |
|
Sets the current table used in the 32-bit | |
|
Initializes the 32-bit Merseene Twister generator
| |
|
Retrieves the current table used in the 64-bit
| |
|
Sets the current table used in the 64-bit | |
|
Selects the uniform (0, 1) multiplicative congruential pseudorandom number generator. | |
|
Initializes a random seed for use in the IMSL random number generators. | |
|
Generates pseudorandom numbers from a uniform (0, 1) distribution. | |
|
Generates a pseudorandom number from a uniform (0, 1) distribution. |
S
|
Adds a scalar to each component of a vector, x ¬ x + a, all single precision. | |
|
Sums the absolute values of the components of a single-precision vector. | |
|
Computes the scalar times a vector plus a vector,
| |
|
Exits ScaLAPACK mode for the IMSL Library routines. | |
|
Calculates the row and column dimensions of a local distributed array based on the size of the array to be distributed and the row and column blocking factors to be used. | |
|
Maps array data from a global array to local arrays in the two-dimensional block-cyclic form required by ScaLAPACK routines. | |
|
Reads matrix data from a file and transmits it into the two-dimensional block-cyclic form required by ScaLAPACK routines. | |
|
Sets up a processor grid and calculates default values for use in mapping arrays to the processor grid | |
|
Unmaps array data from local distributed arrays to a global array. | |
|
Writes the matrix data to a file. | |
|
Sums the absolute values of the real part together with the absolute values of the imaginary part of the components of a complex vector. | |
|
Computes the Euclidean norm of a complex vector. | |
|
Copies a vector x to a vector y, both single precision. | |
|
Computes the sum of a single-precision scalar, a single-precision dot product and the double-precision accumulator, which is set to the result ACC ¬ ACC + a + xTy. | |
|
Computes the sum of a single-precision scalar plus a singleprecision dot product using a double-precision accumulator, which is set to the result ACC ¬ a + xTy. | |
|
Computes the single-precision dot product xTy. | |
|
Computes the sum of a single-precision scalar and a single precision dot product, a + xTy, using a double-precision accumulator. | |
|
Computes one of the matrix-vector
operations: | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes one of the matrix-vector
operations: | |
|
Computes the rank-one update
of a real general matrix: | |
|
Prints rank-1 or rank-2 arrays of numbers in a readable format. | |
|
Computes the Hadamard product of two single-precision vectors. | |
|
Computes the inverse Laplace transform of a complex function. | |
|
Calculates the indices of eigenvalues of a Sturm-Liouville problem with boundary conditions (at regular points) in a specified subinterval of the real line, [a, b]. | |
|
Determines eigenvalues, eigenfunctions and/or spectral density functions for Sturm-Liouville problems in the form with boundary conditions (at regular points). | |
|
Solves a sparse linear programming problem via the revised simplex algorithm. | |
|
Computes the Euclidean length or L2 norm of a single-precision vector. | |
|
Sorts a rank-1 array of real numbers x so the y results are algebraically nondecreasing, y1 £ y2 £ ¼ yn. | |
|
Computes the values of a spline that either interpolates or fits user-supplied data. | |
|
Returns the derived type array result. | |
|
Weighted least-squares fitting by B-splines to discrete One-Dimensional data is performed. | |
|
Returns an array result,
given an array | |
|
Multiplies the components of a single-precision vector. | |
|
Searches a sorted vector for a given scalar and return its index. | |
|
Applies a Givens plane rotation in single precision. | |
|
Constructs a Givens plane rotation in single precision. | |
|
Applies a modified Givens plane rotation in single precision. | |
|
Constructs a modified Givens plane rotation in single precision. | |
|
Computes the matrix-vector
operation | |
|
Multiplies a vector by a scalar, y ¬ ay, both single precision. | |
|
Sets the components of a vector to a scalar, all single precision. | |
|
Searches a character vector, sorted in ascending ASCII order, for a given string and return its index. | |
|
Subtracts each component of a vector from a scalar,
| |
|
Sums the values of a single-precision vector. | |
|
Interchanges vectors x and y, both single precision. | |
|
Computes one of the matrix-matrix
operations: | |
|
Computes the matrix-vector operation | |
|
Computes the rank-one update
of a real symmetric matrix: | |
|
Computes the rank-two update
of a real symmetric matrix: | |
|
Computes one of the symmetric rank 2k
operations: | |
|
Computes one of the symmetric
rank k operations: | |
|
Computes one of the matrix-vector
operations: where A is a triangular matrix in band storage mode. | |
|
Solves one of the triangular systems: | |
|
Computes one of the matrix-matrix operations: | |
|
Computes one of the matrix-vector operations: | |
|
Solves one of the matrix equations: | |
|
Solves one of the triangular linear
systems: | |
|
Sets or retrieves MATH/LIBRARY single-precision options. | |
|
Computes a smooth bivariate interpolant to scattered data that is locally a quintic polynomial in two variables. | |
|
Returns the derived type array result given
| |
|
Weighted least-squares fitting by tensor product
| |
|
Returns a tensor product array result, given two arrays
of | |
|
Multiplies a vector by a scalar and store the result in another vector, y ¬ ax, all single precision. | |
|
Computes the singular value decomposition of a rank-2
or rank-3 array, | |
|
Sorts an integer array by nondecreasing absolute value. | |
|
Sorts an integer array by algebraically increasing value. | |
|
Sorts an integer array by algebraically increasing value and returns the permutation that rearranges the array. | |
|
Sorts a real array by nondecreasing absolute value. | |
|
Sorts a real array by nondecreasing absolute value and returns the permutation that rearranges the array. | |
|
Sorts a real array by algebraically increasing value. | |
|
Sorts a real array by algebraically increasing value and returns the permutation that rearranges the array. | |
|
Computes a single-precision xyz product. |
T
|
Gets today's date. | |
|
Gets time of day. | |
|
Transposes a rectangular matrix. | |
|
Computes a two-dimensional iterated integral. |
U
|
Sets or retrieves input or output device unit numbers. | |
|
Handles MATH/LIBRARY and STAT/LIBRARY type REAL and double precision options. | |
|
Minimizes a function of N variables using a conjugate gradient algorithm and a finite-difference gradient. | |
|
Minimizes a function of N variables using a conjugate gradient algorithm and a user-supplied gradient. | |
|
Minimizes a function of N variables using a modified Newton method and a user-supplied Hessian. | |
|
Minimizes a function of N variables using a modified Newton method and a finite-difference Hessian. | |
|
Minimizes a function of N variables using a modified Newton method and a finite-difference Hessian. | |
|
Minimizes a function of N variables using a quasi-New method and a finite-difference gradient. | |
|
Minimizes a function of N variables using a direct search polytope algorithm. | |
|
Normalizes the columns of a rank-2 or rank-3 array so each has Euclidean length of value one. | |
|
Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian. | |
|
Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a user-supplied Jacobian. | |
|
Finds the minimum point of a nonsmooth function of a single variable. | |
|
Finds the minimum point of a smooth function of a single variable using both function evaluations and first derivative evaluations. | |
|
Finds the minimum point of a smooth function of a single variable using only function evaluations. |
V
|
Computes the convolution of two complex vectors. | |
|
Computes the convolution of two real vectors. | |
|
Obtains IMSL MATH/LIBRARY-related version, system and license numbers. |
W
|
Prints a complex rectangular matrix with a given format and labels. | |
|
Prints a complex rectangular matrix with integer row and column labels. | |
|
Prints an integer rectangular matrix with a given format and labels. | |
|
Prints an integer rectangular matrix with integer row and column labels. | |
|
Sets or retrieves an option for printing a matrix. | |
|
Prints a real rectangular matrix with a given format and labels. | |
|
Prints a real rectangular matrix with integer row and column labels. |
Z
|
Finds the zeros of a univariate complex function using Müller's method. | |
|
Finds a zero of a real function that changes sign in a given interval. | |
|
Finds the zeros of a polynomial with real coefficients using Laguerre's method. | |
|
Finds the zeros of a polynomial with complex coefficients using the Jenkins-Traub three-stage algorithm. | |
|
Finds the zeros of a polynomial with real coefficients using the Jenkins-Traub three-stage algorithm. | |
|
Adds a double complex scalar to the accumulator in extended precision. | |
|
Initializes an extended-precision complex accumulator to a double complex scalar. | |
|
Multiplies double complex scalars using extended precision. | |
|
Stores a double complex approximation to an extended-precision complex scalar. | |
|
Finds the real zeros of a real function using Müller's method. |
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |
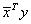 .
.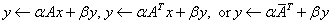 ,
,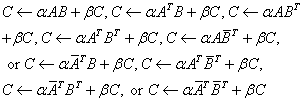
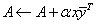 .
.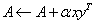 .
.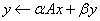 ,where A is an
Hermitian band matrix in band Hermitian storage.
,where A is an
Hermitian band matrix in band Hermitian storage.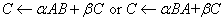 ,
,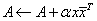 with x complex and
with x complex and 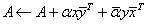 .
.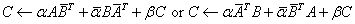 ,
where C is an n by n Hermitian matrix and A
and B are n by k matrices in the first case and
k by n matrices in the second case.
,
where C is an n by n Hermitian matrix and A
and B are n by k matrices in the first case and
k by n matrices in the second case.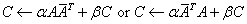 ,
,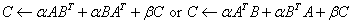 ,
,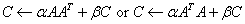 ,
,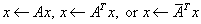 ,
,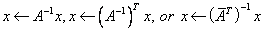 ,
,
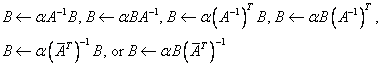
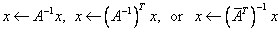
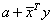 , using a double-precision accumulator.
, using a double-precision accumulator.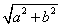 without underflow or
overflow.
without underflow or
overflow.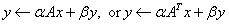 ,
,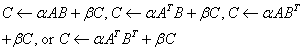 .
.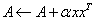 .
.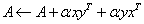 .
.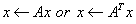 ,
,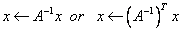 ,
,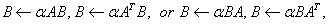

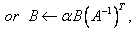
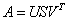 .
.